B2.9 Use the ratios of 1 to 2, 1 to 5, and 1 to 10 to scale up numbers and to solve problems.
Skill: Using Ratios to Solve Problems Involving Proportional Reasoning
The ability to use proportional reasoning is developed throughout the mathematics learning process.
The analysis of proportional relationships is done by applying proportional reasoning. This reasoning comes into play when comparing 2 ratios and recognizing a multiplicative relationship.
In Grade 3 , the study of proportional relationships focuses on recognizing and describing the multiplicative relationship in a variety of problem-solving situations. Students intuitively use proportional reasoning to solve problems involving two quantities that are in a ratio of 1 to many (for example, 1 person for 10 fingers), many to one (for example, 5 people per table) or many to many (for example, 4 litres of juice for 8 people). They also use manipulatives and various models such as diagrams, fractions and number lines.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 50-51.
Example 1
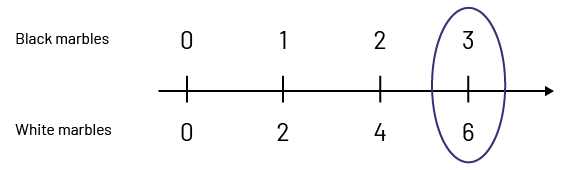
In this set of 9 marbles below, there is a ratio of 1 to 2, \(\frac{1}{2} \) or 1:2 between the number of black marbles and the number of white marbles.

There are 3 black marbles and 6 white marbles. This means that the white marbles are twice the black marbles. Using a double number line, the top number shows a scale by one and the bottom number shows a scale by 2. In this scaling of 1 to 2, we see that the white marbles are always double the black marbles.
Example 2
Teachers ask primary students to determine the number of pieces in 3 chocolate bars if a bar contains 5 pieces (ratio of 1 to 5). This is a multiplicative relationship since the number of pieces is 5 times greater than the number of bars. However, to solve this kind of problem, students will first use repeated addition (\(5 + 5 + 5 \)). Later, when they have been exposed to the concept of multiplication, they can solve it by multiplying (\(3 \times 5 \)), which is a first step towards using proportional reasoning.

\(5 + 5 + 5\) or \(3 \times 5\)
A ratio table can be used to scale up numbers proportionately.
| Chocolate Bars | 1 | 2 | 3 |
|---|---|---|---|
| Ratio 1 to 5 | \(\times 5\) | \(\times 5\) | \(\times 5\) |
| Number of Pieces | 5 | 10 | 15 |
So, in 3 chocolate bars, there are 15 pieces.
In the example above, we easily recognize the multiplicative relationship by 5 between the number of bars and the number of pieces.
Students place ratios on the double number line equivalent to the one given in order to solve the problem. They can choose the ratios according to their needs and understanding of the problem.
Example 3
Abdala buys bread to make sandwiches for the school picnic. The cost of the bread is $2 to make 20 small sandwiches. How much will it cost to make 60 sandwiches?
Using a double number line, the top number shows a scaling by one, which is the cost of bread, and the bottom number shows a scaling by 10, which is the number of sandwiches. The ratio here is 1 to 10 since the multiplicative relationship between 2 and 20 is 10.

The cost of bread for 60 sandwiches is $6.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 50-52.
The multiplicative relationship between two ratios is the basis of proportional reasoning. Ratios are present in everyday life and in several mathematical situations, notably in place values (for example, the ratio between units and tens is 1 to 10), in fractions (for example, \(\frac{ 1}{5} \) or 1:5), in similar figures (for example, a magnification of 1 to 2), in units of measurement of the metric system (for example, the ratio between metres and decimetres is of 1 to 10).
Students should use a variety of models in activities to develop their proportional reasoning skills. Moreover, these informal experiences will be used for further study of ratios, rates, percentages, and algebra in later grades.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 54.
Knowledge: Proportional Reasoning
Proportional reasoning is basically seeing numbers in terms of their relative rather than absolute values.
Source: translated from Qu'est-ce que le raisonnement proportionnel? Document d'appui pour Mettre l'accent sur l'enseignement des mathématiques, p. 3.
The analysis of proportional relationships is done by applying proportional reasoning. This reasoning is used when comparing two ratios and recognizing a multiplicative relationship. Note that multiplicative relationships include the operation of division, since any division can be transformed into multiplication (for example, dividing by 2 is equivalent to multiplying by \(\frac{1}{2}\)).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 50.
Knowledge: Proportional Relationship
There is a proportional relationship between two quantities when these quantities increase or decrease simultaneously by the same factor.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 49.
Knowledge: Ratio
Relationship between two quantities expressed as how much of one thing there is compared to another thing, for exemple, there is 1 dog to 5 cats.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 49.
