B2.6 Represent multiplication of numbers up to 10 × 10 and division up to 100 ÷ 10, using a variety of tools and drawings, including arrays.
Activity 1: Sometimes Upside Down (Array)
Directions
Ask students to represent 5 × 8 and 8 × 5 using arrays.
Here are some possible representations:
Proceed in the same way with various multiplications of 2 numbers.
Intervention
Ask questions to help understand the commutative property of multiplication, such as :
- What do you see?
- How many tokens are there? rows? columns?
- I turn the array (90°). How many are there now?
- What is the product of 5 and 8? What other multiplication fact is similar to it?
- By rotating the arrays, what other pairs of numbers give the same product?
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 42.
Activity 2: Looking for Arrays
Choose a number with several factors, such as 12, 18, 24 or 36.
Project the possible arrays to represent a number. For example, if 18 is chosen, it is possible to arrange 18 tokens in rows and columns as follows: \(1 \times 18 \), \(2 \times 9 \), \(3 \times 6 \), \(18 \times 1 \), \(9 \times 2 \) and \(6 \times 3 \).
Explain the relationship between arrays such as \(6 \times 3 \) and \(3 \times 6 \) (the product is the same, but the arrangement of rows and columns is reversed) and which is called commutative property.
Have students use tokens to create as many arrays as possible to represent the number 12.
Have students write the number sentences to represent each of the arrays created. For example, students can write the following number sentences if the tokens are arranged in 6 rows and 2 columns:
\(2 \times 6 = 12 \)
\(6 \times 2 = 12 \)
\(2 + 2 + 2 + 2 + 2 + 2 = 12 \)
\(12 \div 2 = 6 \)
\(12 \div 6 = 2\)
For each number chosen, list the number sentences written by the students. Point out how the array represents each of the number sentences.
Source: Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 206-207.
Activity 3: The Array
Ask students to find objects that remind them of an array in the classroom or school (for example, tiles, windows, desks in the classroom).
Have them write number sentences that correspond to these arrays and record them on the whiteboard or a large sheet of paper.
Give them problems involving various arrays. For example:
- What are all the possible ways to arrange 24 chairs in rows and columns?
- How can 12 drawings be placed on a bulletin board in arrays?
Ask students to:
- solve problems using manipulatives;
- to write down their solutions and compose number sentences representing their arrays.
Source: Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 207.
Activity 4: Operations Game
Form teams of 2 or 3 and distribute 2 dice and tokens to each.
Ask students to take turns rolling the 2 dice and point out that the numbers rolled represent the number of rows and columns in an array (for example, if the student rolls a 3 and a 5, they make an array of 3 rows and 5 columns or 5 rows and 3 columns).
Ask students to write 3 number sentences using different operations corresponding to the array represented and explain them (for example, \(5 + 5 + 5 = 15 \), \(3 \times 5 = 15 \) and \(15 \div 3 = 5 \)).
Source: Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 208.
Activity 5: Tokens in an Array
Form teams of 2 and give each team a bag containing 30 tokens and a deck of cards prepared using Appendix 3Rel.1 (Number Cards).
Ask students to:
- to draw a card from the bag;
- to represent, with the help of tokens, the number in an array;
- place pencils, straws or pieces of string on the array to represent equal groups of tokens;
- to represent other possible groupings.
Source: Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 205.
Activity 6: Trios - Commutative Property
Materials
This activity is done with the whole class. Each student receives 1 card from the Trios game. Once the cards have been dealt, the students look for the other members of their trio. They need to know the answer to the question, or consider the possible questions to which their card has the answer. For example, the trios could be \(3\; + \;5,\;5\; + \;3\;{\rm{and}}\;{\rm{8}}\); or \(3\; \times \;6,\;6\; \times \;3\;{\rm{and}}\;18\). When a trio is complete, the 3 students sit together. Once all the students are seated, each trio presents the cards to the class.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 78.
Activity 7: Array (Multiplication Facts)
Represent, with students, the basic number facts being studied using the arrays. Collectively create a large poster that illustrates the basic number facts.
The poster can be created with different colours.
Ask students to identify patterns and connections between products.
The multiplication table is represented in 2 ways.
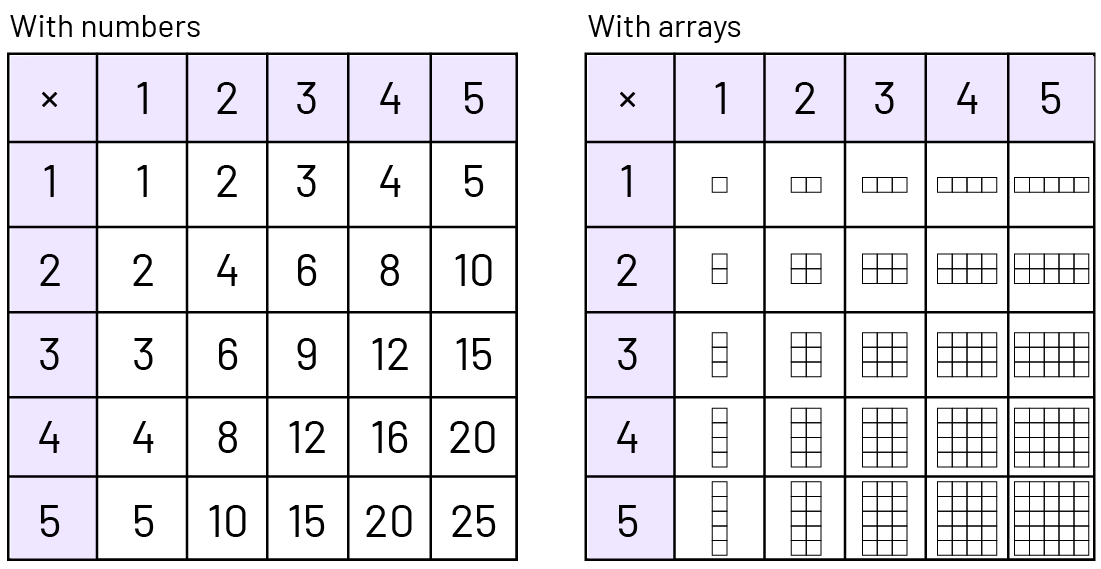
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).