B2.8 Represent the connection between the numerator of a fraction and the repeated addition of the unit fraction with the same denominator using various tools and drawings, and standard fractional notation.
Activity 1: Counting in Unit Fractions
One person on the team chooses a unit fraction (for example, \(\frac{1}{5}\))
The first person says “1 one fifth”, the second person says “2 one fifths”, the third person says “3 one fifths” and so on…
When a person gets to a whole number (for example, "5 one fifths"), that person should stand up and say the equivalent whole number.
Be sure to count well beyond 1.
The student who is standing when all other students are sitting wins the game.
Activity 2: In Kindergarten
Example 1
In a kindergarten class, the students in your class help the younger students count to 10 using objects. You decide to use small plastic animals and place them on a ten frame. The teacher circulates and asks you to analyze the items in this set as fractions.
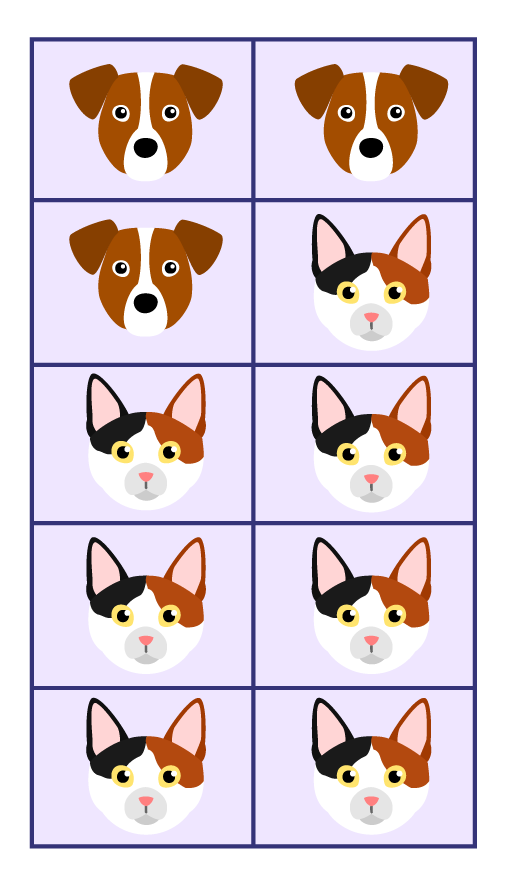
Strategy
Using a Set Model
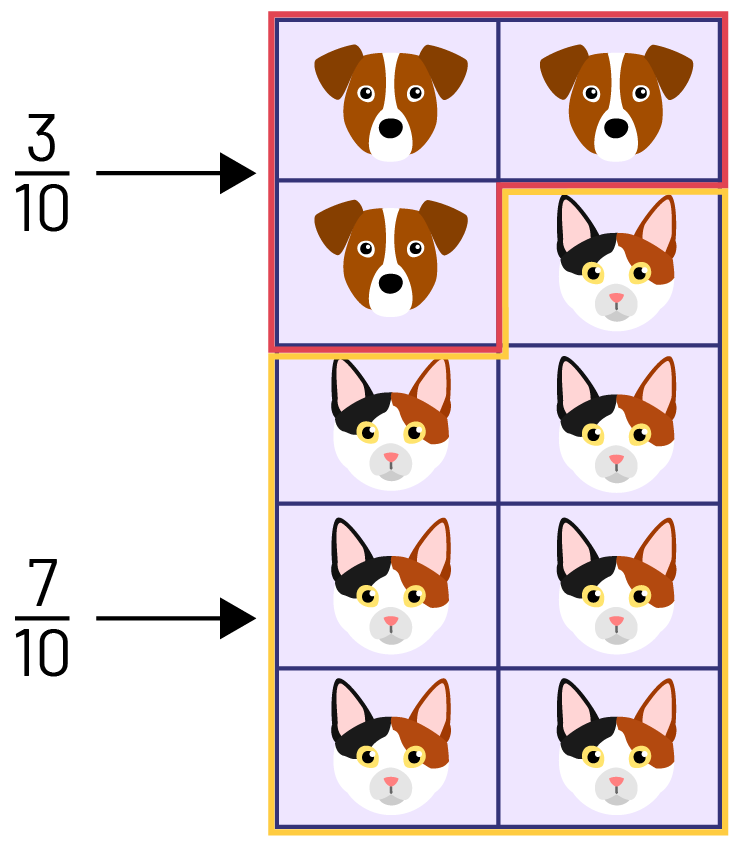
The frame is complete with 10 animals, which represents the whole. Each dog or cat represents one tenth (\(\frac{1}{10} \)) of the animals. There are 3 dogs. I count them in unit fractions: “1 one tenth”, “2 one tenths”, “3 one tenths”. So the dogs are three one tenths of the set of animals, which I can write as \(\frac{1}{10} + \frac{1}{10} + \frac{1}{10} = \frac{3}{10} \). According to this fraction, the 3 is the numerator and it represents the number of dogs. According to this fraction, the 10 is the denominator and it represents the total number of animals.
There are 7 cats. I count them in unit fractions: “1 one tenth”, “2 one tenths”, “3 one tenths”, “4 one tenths”, “5 one tenths”, “6 one tenths”, “7 one tenths”. So, the cats are seven tenths of the set of animals, which I can write as \(\frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} = \frac{7}{10} \). According to this fraction, the 7 is the numerator and it represents the number of cats. According to this fraction, the 10 is the denominator and it represents the total number of animals.
Example 2
Kindergarten students practice colouring boxes on a rectangular strip by choosing colours of their choice. Here is a reproduction of one student sample.

How could you describe the boxes using fractions?
Strategy
Using an Area Model
There are 5 boxes in all; 2 green coloured boxes and 3 boxes that are not coloured. Because there are five boxes in the strip, I know that each box is one fifth of the strip. There are 2 green boxes, so two fifths of the boxes are green, which I can write as \(\frac{1}{5} + \frac{1}{5} = \frac{2}{5} \). In the fraction \(\frac{2}{5} \), the 2 is the numerator and represents the number of green boxes. The 5 is the denominator and it represents the total number of boxes.
There are 3 boxes without colour out of a total of 5 boxes in all, so three one fifths, which I can write as \(\frac{3}{5} \). The 3 is the numerator and represents the number of uncoloured boxes. The 5 is the denominator and it represents the total number of boxes.

Source: translated from En avant les maths! 3e, CM, Nombres, p. 3-5.
