B1.2 Compare and order whole numbers up to and including 10 000, in various contexts.
Skill: Comparing and Ordering Whole Numbers up to 10 000
Benchmark numbers can be used to compare quantities. For example, 132 is less than 500 and 620 is greater than 500, so 132 is less than 620.
Numbers can be compared by their place value. For example, when comparing 8250 and 8450, the greatest place value where the numbers differ is compared. For this example, 2 hundreds (from 8250) and 4 hundreds (from 8450) are compared. Since 4 hundreds is greater than 2 hundreds, 8450 is greater than 8250.
Understanding place value allows us to compare and order numbers. The sequence in which numbers are organized is a stable order, and patterns in this sequence allow predictions about order and comparisons to be made.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8 , 2020, Ontario Ministry of Education.
The number line is a model that supports students' number sense development. A number line does not show the quantity corresponding to the numbers that are placed on it, but it allows us to "see" numbers in relation to each other. For example, a number line with the numbers 5001, 5015, 5100, and 5500 on it represents the order relationship between these numbers.

The development of number sense in the junior grades is linked to the recognition of relationships between numbers, including:
- place value relationships;
- order relationships;
- proportionality relationships.
Exploring these relationships helps students compare numbers.
For example, if students are asked to find similarities, differences, and connections between the numbers 12, 24, 25, 37, 50, 96, 106, and 120, they may point out:
- that all of these numbers, except 106 and 120, have two digits or that 24 and 25 have the same number of tens (place value relationships);
- that the number 120 is the greatest number or that 24 is a little less than 25 (order relations);
- that 24 is the double of 12 or that 25 is half of 50 (proportional relationships).
Order Relationships
The ability to recognize order relationships is acquired by comparing numbers, placing them in ascending and descending order, counting forward/up and backwards/down and analyzing the relative proximity of two numbers.
In the junior grades, students are expected to recognize the order relationship between numbers by comparing them. They can describe the relationship by stating, for example, that 2273 is less than 3942. Examples of strategies to compare large numbers are outlined on the chart below.
| Students can recognize that 3942 is greater than 2273: | Example |
|---|---|
| by focusing on the highest place value; | Notice that 3000 is greater than 2000. |
| by visualizing or representing important quantities; |
Visualize 3 groups of 1000 and 2 groups of 1000. 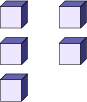 |
| by placing the numbers on a number line; | 
The number 3942 is located to the right of the number 2273. |
| by comparing the numbers in the various positions from the left. | 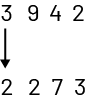
The 3 represents 3000 while the 2 represents 2000. |
To help students develop the skill of recognizing order relationships among large numbers, teachers may ask them to count up from a certain number by 1 (for example, 2998, 2999, 3000, 3001…) or down by intervals (for example, 3200, 3400, 3600…) and count down by 1 (for example, 6271, 6270, 6269…) or by intervals (for example, 5650, 5600, 5550…).
These activities help students recognize that when counting by 1s or by intervals, any named number is greater than those before it and less than those after it, whereas when counting backwards by 1s or by intervals, any number named is less than those before it and greater than those after it. While these relationships may seem obvious to adults, students often get them wrong because they do not consider the concept of regrouping. For example, when asked what number comes before 300, many students tend to spontaneously answer 399 because their attention is focused on the two 0's; they know that a number ending with two 0's is always preceded by a number ending with two 9s, and they forget to consider the regrouping by hundreds that occurs in our place value system. In contrast, when the same problem is posed in context, students are more likely to give thoughtful answers. For example, in a situation where a child has 300 hockey cards and loses one of them, students will easily answer that they have 299 cards left.
Errors related to the concept of grouping are also common when rounding where it is necessary to identify a range. For example, some students will say that 2497 is between 2490 and 2400 instead of 2500. Using a homemade abacus or odometer (created with a paper towel roll and the template) helps students compare numbers, count in intervals, and discover changes related to grouping by tens, hundreds…


Once students have mastered the relationships greater than and less than, they need to learn to clarify these relationships by using their understanding of quantity. They then use expressions such as close to, about, the same as, much more than, and a little less than. For example, students may say that the population of a village of 5239 is about 5000; that 304 is a little more than 300; that 2894 is a little less than 3000; that 3523 is about a hundred more than 3432; and that 620 and 618 are closer together than 630 and 680.
This ability to specify number order relationships becomes important when students use numbers in problem solving, rounding, estimating and comparing. The following activity allows students to demonstrate this skill.
Draw a number line on the board to represent any range (for example, 1000 to 2000). Place some letters (for example, A, B, C, D) in this range as shown below.

Ask a few students to come and locate some numbers on the line (for example, 1873, 1332, 1167). Then ask them to describe the ordering relationships that exist between the numbers and the letters.
For example, students might say:
- that 1167 lies between A and B;
- that the letters B and C are between 1167 and 1332;
- that the number 1873 is closer to 2000 than to the letter D;
- that the letter B seems to be more in the center of the interval between 1000 and 1500 than the letter C.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 43-48.
