B1.9 Describe relationships and show equivalences among fractions and decimal tenths, in various contexts.
Skill: Describing Relationships and Showing Equivalences Between Fractions and Decimal Tenths, in Various Contexts
It is important to recognize equivalencies between various representations of numbers or numerical forms. In the context of decimal numbers, students must recognize the relationship between a decimal number and its equivalent fraction. In Grade 4, students learn about the relationships between decimal tenths and fraction tenths.
Students need to understand that since decimal notation is just another way of representing a decimal fraction, it is then possible to establish a relationship between the two notations (for example, \(\ 0.3 = \frac{3}{10} \)). By recognizing this equivalence, they are able to associate a place value with each of the decimal places that make up a decimal number, for example, tenths.
Example
Students who do not understand this association are sometimes inclined to represent a fraction such as \(\frac{2}{5}\) with 0.2 or 0.25. The following description describes observable behaviors of students who have developed a conceptual understanding of numbers and the relationship between their different representations.
Conceptual Understanding of Numbers
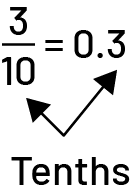
Number: 0.3
Observable behaviours:
- The student can read it (three tenths).
- The student can write the number in fractional notation, that is \(\frac{3}{{10}}\).
- The student can represent the number using concrete materials or visuals.
Example
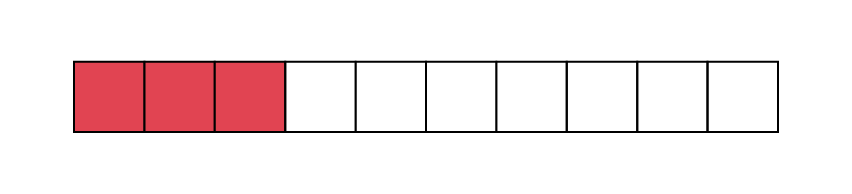
Number: \(\frac{6}{{10}}\)
Observable behaviours:
- The student can read it (six tenths).
- The student can write the number in decimal notation, that is 0.6.
- The student can represent the number using concrete materials or visuals.
Example

Number: \(\frac{2}{7}\)
Observable behaviours:
- The student can read it (two sevenths).
- The student knows that the fraction \(\frac{2}{7}\) is not represented by 0.2 because they know that \(\ 0.2 = \frac{2}{10}\).
To establish the relationship between a fraction with a denominator that is not a multiple of ten (for example, \(\frac{1}{4}\)) and the corresponding decimal number, it is necessary to use the concept of equivalent fractions. For example, students can use strips of equal lengths as shown below to see that \(\frac{1}{4}\) is between \(\frac{2}{{10}}\) and \(\frac{3}{{10}}\).
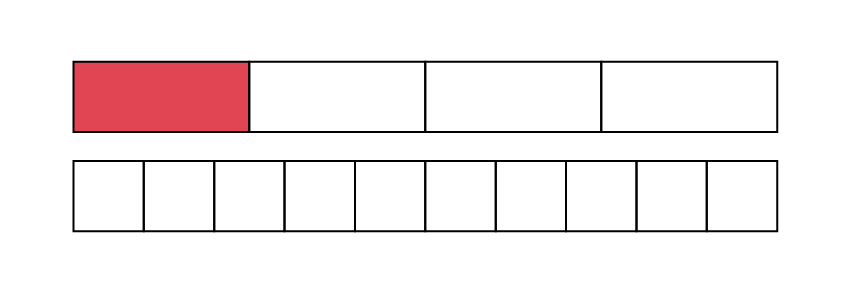
This type of example allows students to recognize that fractions with an equivalent decimal fraction are both represented by the same decimal number. This is especially true of fractions expressed in halves and fifths as the following table demonstrates.
| Fraction | Equivalent Decimal Fraction | Decimal Number |
|---|---|---|
| \(\frac{1}{2}\) | \(\frac{5}{{10}}\) | \[0.5\] |
| \(\frac{2}{5}\) | \(\frac{4}{{10}}\) | \[0.4\] |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 46-48.
Knowledge: Decimal Number
A decimal number is a number that can be expressed in decimal notation with a finite decimal part.
Example
\(3.72\) and \({\rm{12}}{\rm{.135}}\;{\rm{64}}\)
Decimal numbers include all whole numbers, because whole numbers can be expressed with a decimal part.
Example
\(3\; = \;3.0\)
It also includes some fractions, such as \(\frac{2}{5}\) and \(\frac{3}{{16}}\), since \(\frac{2}{5} = 0.4\) and \(\frac{3}{{16}} = 0.187\;5\). Note that \(\frac{1}{2}\),\(\frac{5}{{10}}\) and 0.5 are symbolic representations of the same decimal number.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 28.
Knowledge: Decimal Fraction
All decimal numbers can be expressed as decimal fractions, that is, fractions whose denominator is a power of 10.
Example
\(3.7\; = \;3\frac{7}{10}\; = \frac{37}{10}\)
\(5\; = \;5.0\; = \frac{5}{1}\)
Note: The powers of 10 are 1, 10, 100, 1000… We include 1 as a power of 10, because 100 = 1.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 28.
