B2.3 Use mental math strategies to multiply whole numbers by 10, 100, and 1000, divide whole numbers by 10, and add and subtract decimal tenths, and explain the strategies used.
Skill: Using Mental Math Strategies to Multiply Whole Numbers by 10, 100 and 1000
The importance of mental math to multiply by 10, 100 and 1000 and divide by 10 is connected to the relationships that exist between place values. In order to represent this relationship, a place-value mat can be used.
Multiplying a whole number by 10 can be visualized as a shifting of the digit(s) to the left by one column on a place-value mat.
For example,
\( 3 \times 10\)

The student can also visualize 3 rods of \(1 \times 10\) to perform the multiplication \(3 \times 10\).
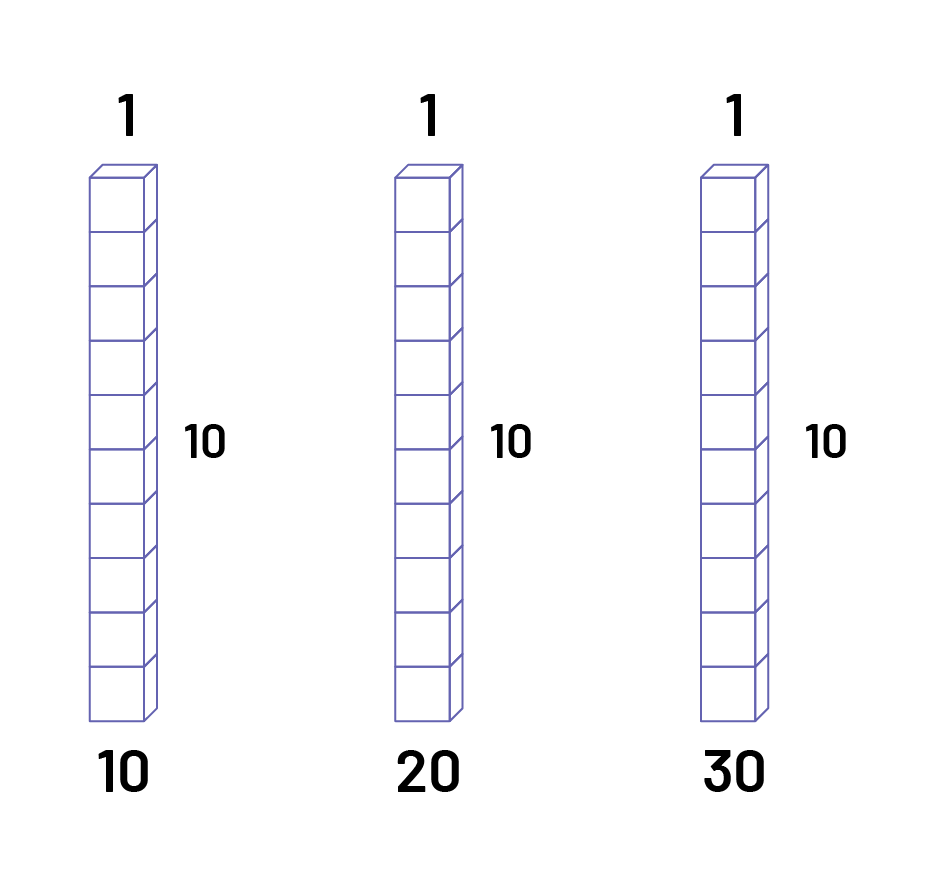
Then the product of 3 × 10 is 30.
Multiplying a whole number by 100 can be visualized as a shifting of the digit(s) to the left by two columns on the place-value mat.
For example,
\(\ 3 \times 100\)

The student can also visualize 3 flats of \(\ 10\; \times 10\) to perform the multiplication \(\ 3 \times 100\).
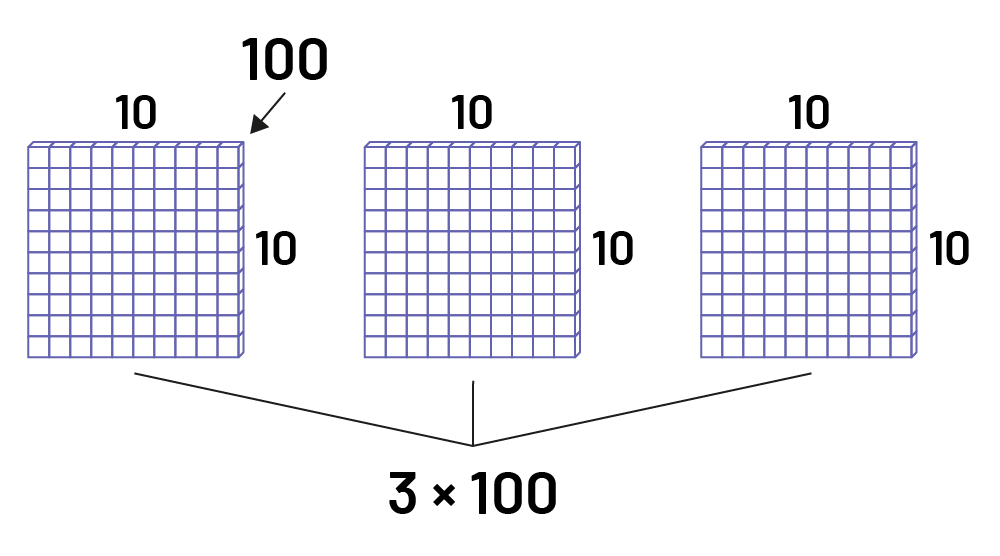
Then the product of \(\ 3 \times 100\) is 300.
Multiplying a whole number by 1000 can be visualized as a shifting of the digit(s) to the left by three columns on the place-value mat.
For example,
\(\ 3 \times 1\;000\)

The student can also visualize 3 large cubes of \(\ 10 \times 10 \times 10\) to perform the multiplication \(\ 3 \times 1\;000\).

Then the product of \(\ 3 \times 1\;000\) is 3000.
Skill: Using Mental Math Strategies to Divide a Whole Number by 10
The importance of mental math to divide by 10 is connected to the relationships that exist between place values. In order to properly represent this relationship, a place-value mat can be used.
Dividing a whole number by 10 can be visualized as a shifting of the digit(s) to the right by one column on the place-value mat.
For example,
\(\ 210 \div 10\)

The student can also visualize 2 rods of \(\ 10 \times 10\) to perform the division \(\ 210 \div 10\). They can decompose 210 into 100 + 100 + 10 and then divide each by 10.
There is one group of 100 that is decomposed into 10 groups of 10.
There is another group of 100 that is decomposed into 10 groups of 10.
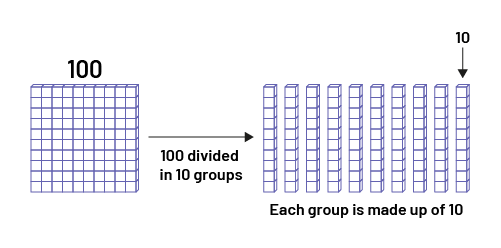
There is another group or 10 that is decomposed into 10 groups of 1.
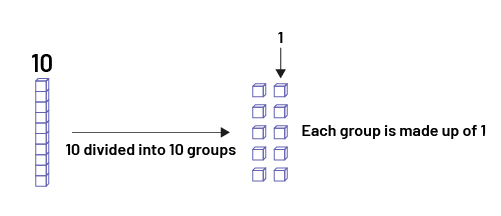
The quotient of the division \(210 \div 10\) is 21.
Students should understand the effect of multiplication and division by 10 and multiples of 10. The explanation of these operations often boils down to the statement, "When you multiply by 10, you add a 0 and when you divide by 10, you take away a 0." This statement is not recommended because it does not take into account the understanding of operations and students are encouraged to apply a mechanical shortcut without being able to make a connection during multiplication or division by numbers such as 10, 100, or 1000.
It is helpful for students to recognize that computations such as \(5\; \times \;10\) can be thought of as \(5 \times 1\) tens and \(130 \div 10\) can be thought of as 13 tens ÷ 1 ten. We can then better understand the appearance or disappearance of the digits " 0 " in the computations.
| Operation | Interpretation | Result |
|---|---|---|
|
\(5 \times 10\) |
\(5 \times 1\) ten      |
5 tens is 50 |
|
\(130 \div \;10\) |
130 separated in groups of 10              |
13 |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 91-92.
Skill: Using Mental Math Strategies to Add and Subtract Decimal tenths, and Explain the Strategies Used
To add decimal numbers effectively, students need to understand the place value of the digits that make up each number and factor this into their calculations. Students must also recognize that the decimal point is a marker that identifies the place value of the digits.
When adding decimal numbers, the concept of grouping is used just as when adding whole numbers. For example, just as one can add 3 hundreds to 8 hundreds to form 11 hundreds, one can add 3 tenths to 8 tenths to form 11 tenths. Since the decimal system does not allow two digits to be placed in the same position, students need to understand the concept of regrouping.
|
Hundreds |
Tens |
Ones. |
Tenths |
|---|---|---|---|
|
0. |
3 |
||
|
0. |
8 |
||
|
1. |
1 |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 98.
During subtraction, it is important, as it was with addition, to consider the place value of the digits that make up the numbers. The strategies for subtracting decimal numbers are essentially the same as those used for subtracting whole numbers.
The student may conclude that one and one tenth is the same as eleven tenths. Using words, it is easier to perform the subtraction of eleven tenths minus eight tenths, which results in 3 tenths.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 101.
Mental Math
Everyday life presents many opportunities to perform computations with decimal numbers. For example, shopping and measuring involve decimal numbers. Estimation skills and mental computational skills are characteristics of number sense and operations sense. A variety of mental computational strategies can be used including rounding, decomposition, and compensation, among others. Here are some examples of their use in mental math situations.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 91.
Example
Annie wants to know how much wood to buy to build a dog house for her dog. The doghouse measures:
1.2 m in height
1.7 m in length
0.6 m in width
Estimation:
\(\begin{align}1.2 + 1.7 + 0.6 &\approx 1 + 2 + 1 \\ &\approx 4 \end{align}\)
Strategy: Addition Using Compensation
I know that 0.8 + 0.2 = 1 so I mentally move 0.7 and 0.1 to 1.2, which means: I then have 2 plus 1 and 5 tenths.

Strategy: Addition Using Decomposition and Compensation
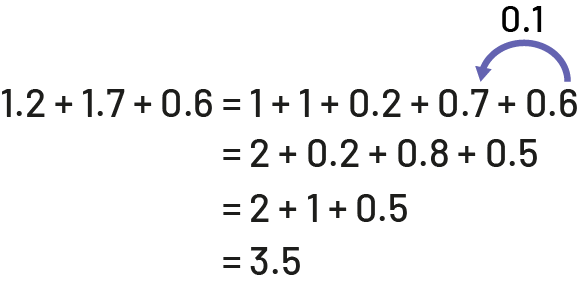
Example
Casimir's dog gave birth to 2 puppies. The vet explains that puppies must weigh at least 24.7 kg when they are six months old to be healthy. Casimir wants to know how much more each puppy should weigh. The first puppy weighs 3.8 kg and the second puppy weighs 4.4 kg.
Estimation:
Puppy 1: \(\begin{align}24.7 - 3.8 &\approx 25 - 4\\ &\approx 21 \end{align}\) Puppy 2: \(\begin{align}24.7 - 4.4 &\approx 25 - 4\\ &\approx 21 \end{align}\)
Strategy: Subtraction Using Decomposition
I mentally broke down each term into ones and tenths.
\(\begin{array}{l}24.7 - 3.8 = (23 - 3) + \left( {1.7 - 0.8} \right)\\\quad \quad \quad \quad \;\, = 20 + 0.9\\\quad \quad \quad \quad \;\; = 20.9\;{\rm{kg}}\quad \quad \end{array}\) \(\begin{array}{l}24.7 - 4.4 = (24 - 4) + \left( {0.7 - 0.4} \right)\\\quad \quad \quad \quad \;\, = 20 + 0.3\\\quad \quad \quad \quad \;\; = 20.3\;{\rm{kg}}\quad \quad \quad \end{array}\)
The mass of puppy 1 must increase by 20.9 kg.
The mass of puppy 2 must increase by 20.3 kg.
Strategy: Compensation Using the Number Line
Puppy 1:
I placed 24.7 and 3.8 on the number line and represented the distance between the two numbers with a rectangle. To make subtraction easier, I mentally moved my rectangle left to 3. My rectangle moved by 0.8 at both ends. Since the size of my rectangle remains unchanged, the gap remained the same, so the right end is now 23.9. My subtraction becomes \(\ 23.9 - 3\).
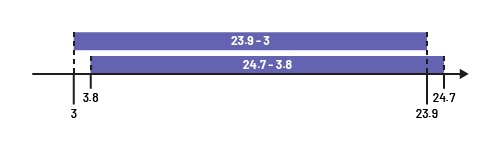
\(\begin{array}{l}24.7 - 3.8 = (24.7 - 0.8) - \left( {3.8 - 0.8} \right)\\\quad \quad \quad \quad \;\, = 23.9 - 3\\\quad \quad \quad \quad \;\; = 20.9\;{\rm{kg}}\quad \end{array}\)
It is much easier to take 3 ones from 23.9.
\(\ 23.9 - 3 = 20.9\)
The mass of puppy 1 must increase by 20.9 kg.
