B2.4 Represent and solve problems involving the addition and subtraction of whole numbers that add up to no more than 10 000 and of decimal tenths, using appropriate tools and strategies, including algorithms.
Skill: Representing and Solving Addition and Subtraction Problems Using Strategies Including Algorithms
The learning of mathematical operations takes place gradually. The starting point should be the exploration of operations in problem-solving situations. Students learn to associate situations with particular operations, which allows them to begin to make sense of the operations. In addition, students need to use strategies based on their understanding of the context, the problem, and the operations. Students become aware that there are many ways to solve a problem and even many ways to carry out the same operation. Subsequently, students should be asked to solve a variety of problems in order to progress to using effective strategies.
Contrary to the traditional process where students mainly learn to apply the usual algorithms, the learning of operations should focus more on understanding operations, exploring mental calculation and using various strategies to carry out operations.
So that they develop effective strategies, it is important that students are offered a variety of problem types that will help them to grasp the multiple meanings of the operations. A well-chosen problem and the application of a well-thought strategy are more beneficial than a series of exercises completed mechanically. It's important to allow sufficient time for students to understand and consolidate their strategies.
Written Problems: Addition and Subtraction
In addition and subtraction, quantities are joined, separated, combined or compared. In order for students to understand the connections between quantities in each of these cases, it is important that they be presented with a variety of problem types.
Addition and subtraction are operations that can be used to solve problems. It is important to avoid referring to problems as "subtraction problems" or "addition problems" because it is the understanding of the situation that leads to the choice of using addition or subtraction to solve it. Thus, students must analyze the problem, choose a strategy (operation) and apply it, just as adults do. In this context, the teacher's role is to assist students in their analysis and understanding of operations.
It is important to note that the problems presented below appear similar because of their context. However, for students, each situation represents a particular problem. It is through experience with these different types of problems that students will become proficient with addition and subtraction.
Join Problem
The part-whole model can be useful for representing known and unknown values in joining problems. The set model is useful for representing the addition of a quantity.
- Change situation: Result (Final quantity) unknown - Jamil has a bag of 600 candies. He buys 500 more pieces of candy. How much candy does Jamil have now?
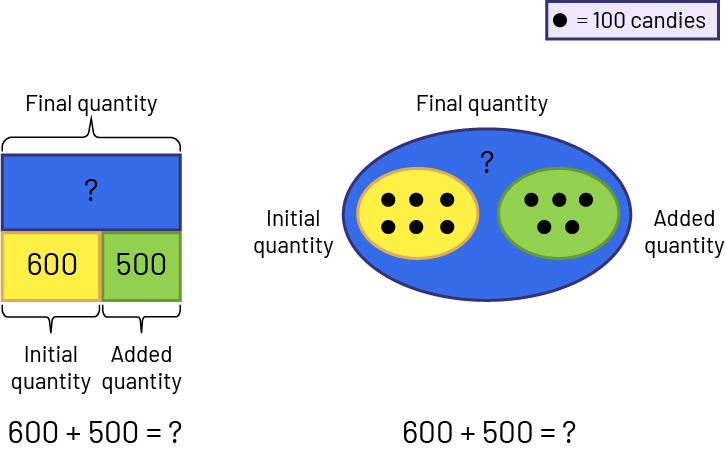
- Change situation: Start (Initial quantity) unknown - Jamil has many candies. He buys 500 more. He now has 1100. How many pieces of candy did Jamil have to start?

- Change situation: Change (Added quantity) unknown - Jamil has a bag of 600 candies. He buys many more. He now has 1100 pieces. How much candy did Jamil buy?

Separate Problems
The part-whole model can be useful for representing known and unknown values in separating problems. The set model is useful for representing the removal of a quantity.
- Separating: Result (Final quantity) unknown. Nadia has $1500. She gives $500 to her brother. How many dollars does she have left now?
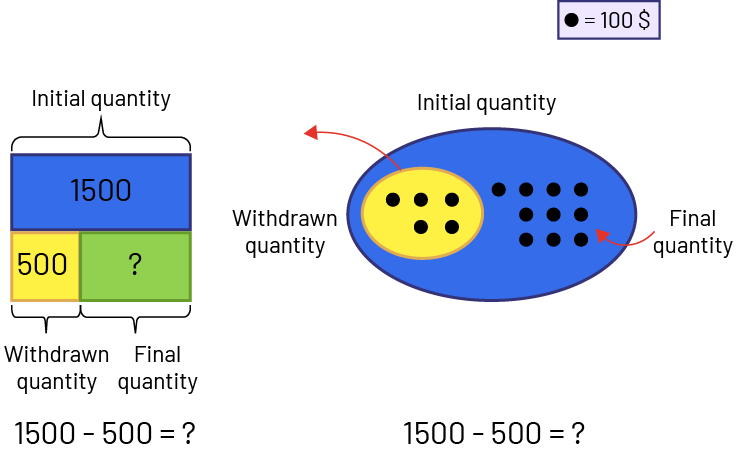
- Separating: Change (Withdrawn quantity) unknown - Nadia has $1500. She gives some to her brother. She now has $1000 left. How much money did Nadia give to her brother?

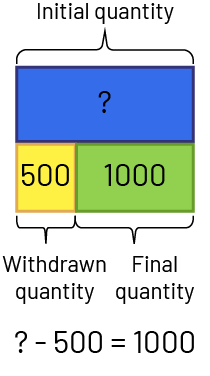
- Separating: Start (Initial quantity) unknown - Nadia had a certain amount of money. She gave $500 to her brother. She now has $1000 left. How much money did Nadia have at the beginning?
Combine (Part-Part-Whole) Problems
The part-whole model can be useful for representing known and unknown parts or the known and unknown whole in combining problems.
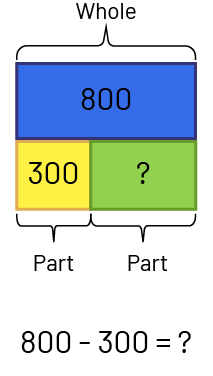
- Combining: Part unknown - The class has 800 colored pencils, and 300 of those pencils are red. The remaining crayons are blue. How many blue crayons does the class have?
- Combining: Whole unknown - The class has a lot of colored pencils. There are 300 red crayons and 500 blue crayons. How many crayons does the class have?
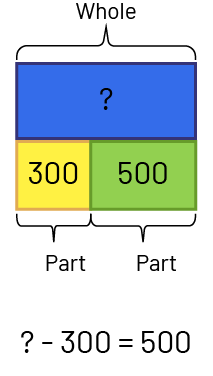
Compare Problems
The linear model can be useful for representing the difference between two numbers in comparing problems. In this example, we use relational rods and a double number line.
- Comparing: Difference unknown. Judith has $600 and Jeanne has $300. How many more dollars does Judith have than Jeanne? OR Judith has $600 and Jeanne has $300. How much less does Jeanne have than Judith?
I know that the dark green rod represents 6 (hundreds), so I placed it at the top of the number line starting at 0. I know that the lime green rod represents 3 (hundreds), so I placed it below the number line starting at 0. I compared the two rods and saw that the lime green rod is 3 (hundreds) less than the dark green rod. I found the difference or gap between the two quantities. There is a difference of $300. Judith has $300 more than Jeanne or Jeanne has $300 less than Judith.
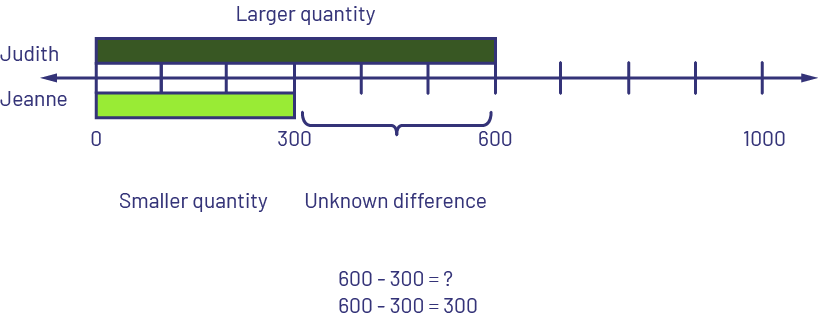
- Comparing: Larger quantity unknown - Judith has $300 more than Jeanne. Jeanne has $300. How many dollars does Judith have? OR Jeanne has $300 less than Judith. Jeanne has $300. How many dollars does Judith have?
I know that the lime green rod represents 3 (hundreds), so I placed it at the top of the number line starting at 0. I took another lime green rod and placed it under the number line starting at 0 and added another lime green rod since Judith has $300 more than Jeanne. I replaced the two lime green rods with the dark green rod that represents 6 (hundreds). Judith has $600.
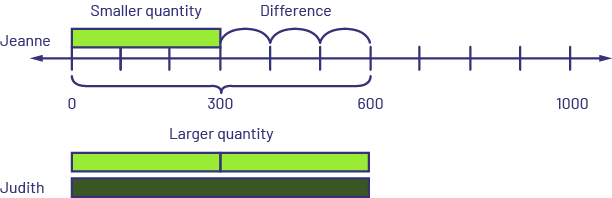
- Comparing: Smaller quantity unknown - Judith has $600 and Jeanne has $300 less than Judith. How many dollars does Jeanne have? Or Jeanne has $300 less than Judith. Judith has $600. How many dollars does Jeanne have?
I know that the dark green rod represents 6 (hundreds), so I placed it at the top of the number line starting at 0. On the number line, I counted backwards three jumps to 300 to represent that Jeanne has $300 less than Judith. I took a lime green rod, which represents 3 (hundreds), and placed it under the number line starting at 0 and ending at 300. Jeanne has $300.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 7-10.
Change situations are perceived by students as active situations, easier to model and "see" as a quantity changes. Combining problems, however, assume a static situation, as no action or change occurs, making them more abstract and difficult to understand. Comparing problems, on the other hand, deal with the relationship between two quantities by finding the difference between them: thus, there is no action, but a comparison of one quantity to another.
Since students are regularly exposed to problems where the result is sought, they find these kinds of problems easier to solve and have more difficulty solving problems where the starting point is unknown or the change is unknown. These variations of problems help develop a more solid understanding of addition and subtraction and the connections between them. For example, in joining problems where the starting point is unknown, students can more easily see the benefits of addition (for example, \(?\; + \;12\; = \;37\)) that keeps the order of action in the problem. This allows them to use a strategy (for example, counting up or counting down) to determine the starting point quantity. These students demonstrate their understanding of the problem and their ability to use a strategy to solve it. However, they do not demonstrate an understanding of the meaning of difference (and subtraction). If they had used subtraction, that is, \(37\; - \;12\; = \;?\), they would have demonstrated a broader understanding of the relationship between quantities in relation to this operation. But when students are learning, there is no need to impose a strategy on them.
Requiring students to subtract will not help those who do not see the relevance of this strategy. However, if they are regularly exposed to a variety of problems and participate in the math exchanges that follow, they will be able to see the connections between various strategies and learn a variety of strategies. They then become more successful.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 83-84.
Computational Strategies
Developing computational strategies offers several advantages over traditional instruction focused on standard algorithms, starting with the pride and confidence they provide. Students who use student-generated algorithms make fewer mistakes because they understand what they are doing. In addition, students improve their knowledge and understanding of the base ten system, on which most computational strategies are based.
Furthermore, Van de Walle and Lovin (2006, p. 40) point out that research shows that students who have been able to develop personal computational strategies perform as well as or better than others on standardized tests.
There are disparities between student-generated algorithms and standard algorithms, including the number of steps or time they take. Student-generated algorithms are usually oriented in a horizontal arrangement in the direction of the units (for example, in the addition 323 + 20, I add 2 tens to 323, which is 343) whereas standard algorithms often use a vertical format and tend to use the units without regard to their position (for example, in the addition \(323; + \;20\), we do: \(3\; + \;0\) is 3; and \(2\; + \;2\) is 4…).
Standard algorithms usually start on the right, whereas in student-generated algorithms, students often start on the left, allowing them to maintain a sense of the size of the quantities involved. Since a student-generated algorithm is a product of each student's imagination and understanding, it remains very flexible so that it can be used in a variety of situations.
In the classroom, it is suggested that several algorithms for a single operation be examined. It is essential that students understand the reasoning behind the actions in these algorithms. Over time, this allows them to choose an effective strategy depending on the context. Teachers with culturally diverse students in their classrooms can invite them to discuss at home the method their parents use to perform addition, subtraction, multiplication or division. These students can present these methods to the class, which can provide new strategies.
The standard algorithms are often presented as the main strategy for doing calculations. Although they are effective, they are not always appropriate. When instruction focuses on the standard algorithm, for example, to calculate \(300\; - \;15\), students tend to pull out a pencil and solve the problem in writing, with the written algorithm using regrouping which is a common source of error. However, it is more efficient to calculate mentally as follows: \(300\; - \;10\; = \;290, and \;290\; - \;5\; = \;285\). Furthermore, the standard algorithm is not the best method to use where estimation is sufficient. Therefore, it is suggested that the standard algorithm be considered as only one of several computational strategies.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 118-119.
Students can solve written problems in a variety of ways. The following tables provide some examples of addition and subtraction algorithms. These are not the only ways to solve a problem, there are many others, so students should be given opportunities to discover other ways of solving problems.
Some algorithms that students can use to determine the sum of 566 + 379 follow.
There are others and they will vary from one group of students to another.
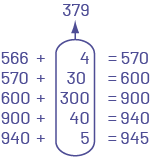
The student proceeds in steps, decomposing the second addend, until a total of 379 is added.
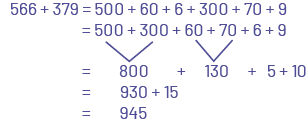
The student decomposes both addends horizontally and then recomposes them by place values.
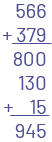
The student groups and adds by place value, starting with the hundreds, then tens and finally ones.
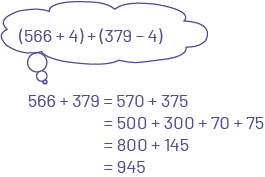
The student uses a compensation technique on the addends to make them easier to work and then decomposes and recomposes them.
The following are examples of algorithms that students can use to determine the difference for 631 - 439 and explain their strategy. There are others and they will vary from one group of students to another.
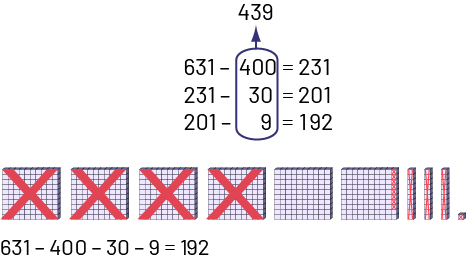
The student decomposes the second term and subtracts it in steps until a total of 439 is taken away.
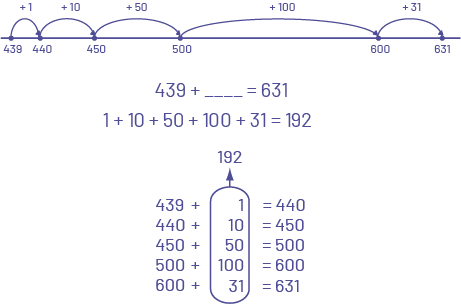
The student adds to subtract by making jumps on a number line, beginning at 439 and ending at 631.
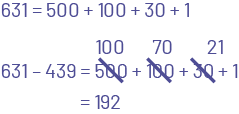
The student decomposes the first term and then subtract the second term, 500 - 400 = 100; 100 - 30 = 70; 30 - 9 = 21, which is recomposed as 100 + 70 + 21 + 1 = 192.
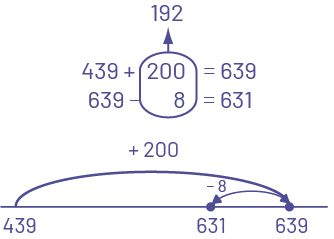
The student uses the number line and records their movements.
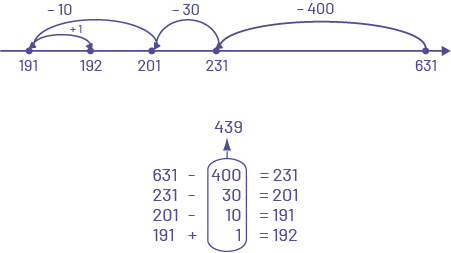
The student uses the number line and counts backwards a total of 439 from 631.
Strategies to Facilitate the Understanding of Standard Algorithms
It is important to provide students with several activities to explore standard algorithms using manipulatives such as the place-value mat, interlocking cubes, ten frames, base ten blocks, number line, and so on.
Teachers should provide students with many opportunities to create their own algorithms, and explain their strategies and reasoning. It is important to give students the opportunity and time to explore algorithms in great depth and engage in discussions about them. It is important to encourage students to work in pairs (one student writes down the steps while the other works with the concrete representation). Understanding the meaning of the steps in a standard algorithm develops when teachers allow students to compare it to their own algorithm in order to make connections between the two approaches, such as "add from left to right and combine.
Adding Multi-Digit Numbers Without Grouping
Adding large numbers can be represented on a number line. For example, students could perform \(435\; + \;223\) by decomposing \(223\;\left( {200\; + \;15\; + \;8} \right)\) and representing the operation as follows:
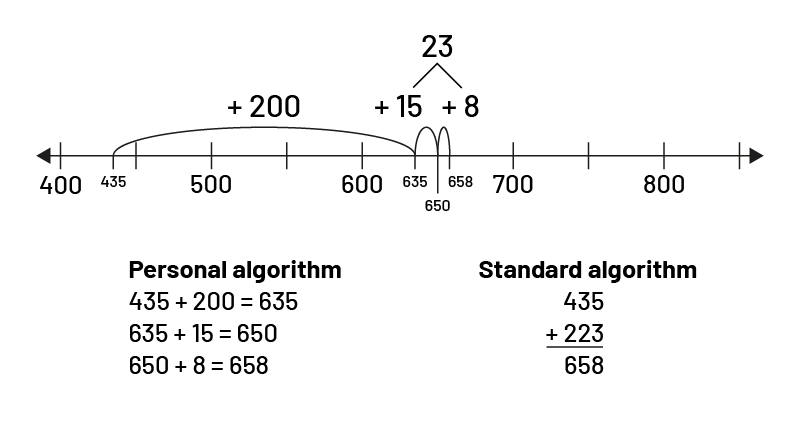
Over time, students gradually develop their sense of abstraction and can use the same strategy without using a number line, but by performing the calculation mentally.
Sources: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 56 and Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 122-123.
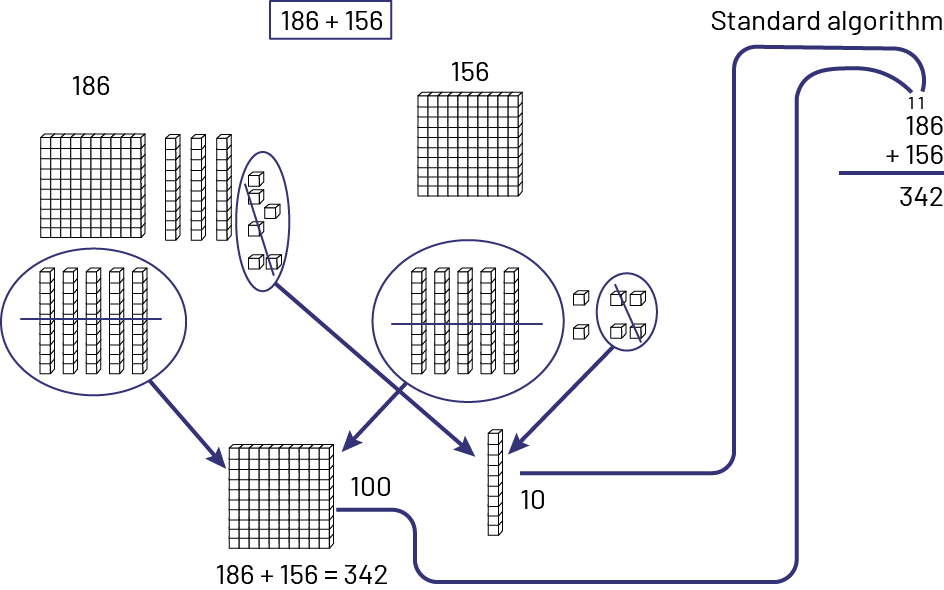
Adding Multi-Digit Numbers with Grouping
(Van de Walle and Folk, 2005, p. 191)
It is important for students to practice exchanging groups of 10 ones into tens, groups of 10 tens into hundreds, and so on. Students need the support of visual representations of groupings to develop a conceptual understanding of the algorithm.
The base ten blocks helps some students visualize the operation more clearly by allowing them to regroup by exchanging ten rods for a flat, for example:
Students can also use a place-value mat that organizes the blocks by the position of the digit in the number.
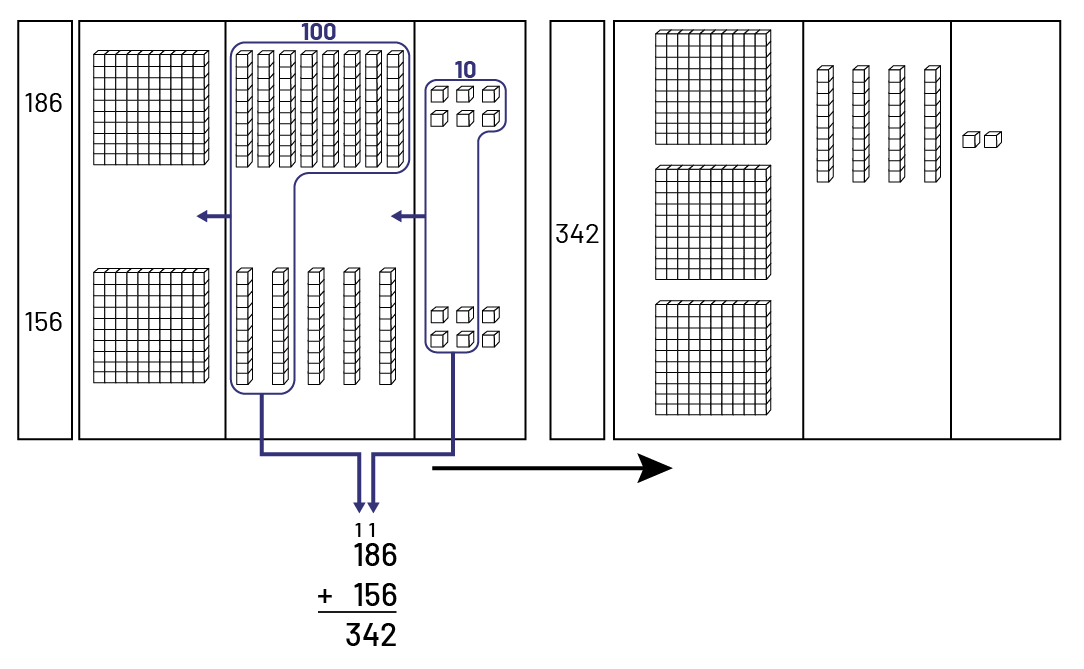
The same numerical expression \(\left( {186\; + \;156} \right)\) can be represented using visuals that a student chooses. In this way, students demonstrate some level of abstraction, since any drawing can represent 100, 10, or 1.

Sources: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 57 and Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 123-124.
Subtraction Without Regrouping
As with addition, students often use manipulatives to perform subtractions. This strategy helps them grasp the concept of separating, although it is not very effective when dealing with large numbers.

The base ten blocks allows students to perform subtraction by separating or removing.
Example
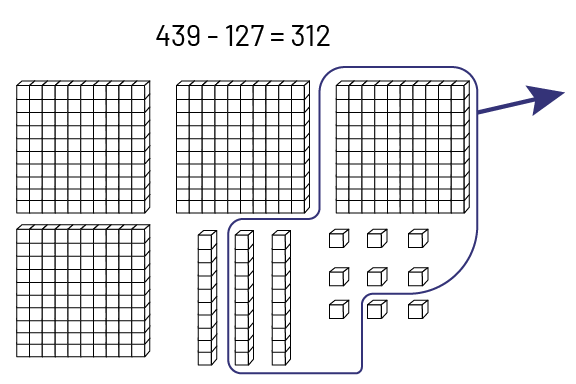
If students use the place value mat for subtraction, some will represent both terms. In this case, subtraction is performed by comparison.
Example
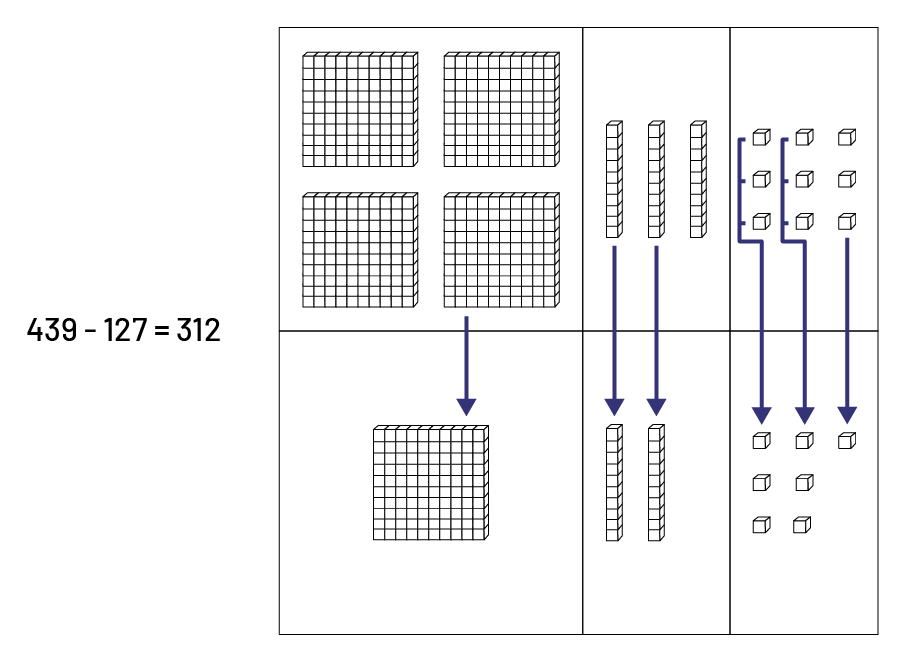
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 127-128.
Subtraction With Regrouping
(Van de Walle and Folk, 2005, p. 193)
Exploring subtraction with regrouping promotes conceptual understanding. Teachers should encourage students to use the place-value mat and base ten blocks to model subtraction with regrouping. Students can work in pairs. They can move on to the written form of the algorithm once they have developed a solid understanding of it through modeling.
In the case of the problem \(325\; - \;118\), students represent the first number (325) with base ten blocks on the top portion of the place-value mat. Unable to remove 8 ones since there are only 5, students exchange one ten for 10 ones.
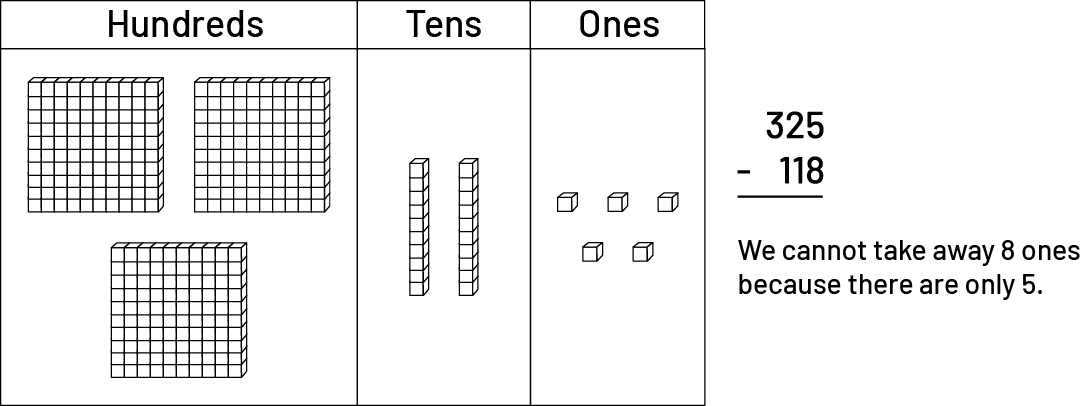

This gives them a group of 15 ones from which they can now remove 8 so that 7 ones remain. Students should be encouraged to group the ones on the mat to better organize their work.

Students now remove 1 ten and 1 hundred and place them outside the mat.

So, \(325\; - \;118\; = \;207\)
Source: adapted and translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 58-59.
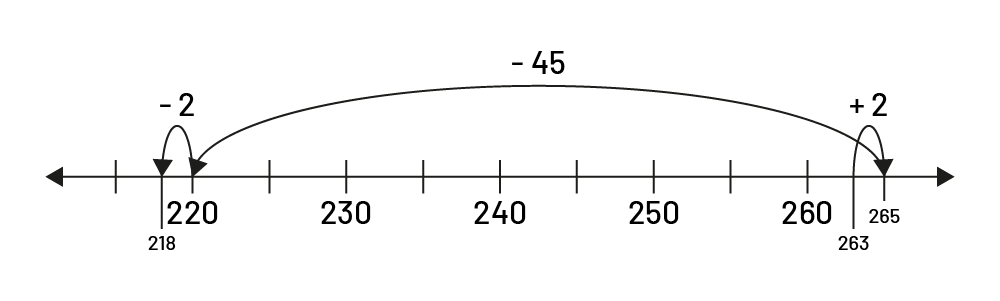
Students can also use the number line to perform a subtraction. For example, to calculate \(263\; - \;45\), they can use compensation to work with "friendlier" numbers. Since \(263\; + \;2\; = \;265\), it is easier to determine \(265\; - \;45\; = \;220\) and then subtract 2 to compensate.
Students can show their thinking on the number line by labelling the jumps:
The number line can also be used with decomposition by removing in jumps according to the place values of the subtrahend, or number being removed:
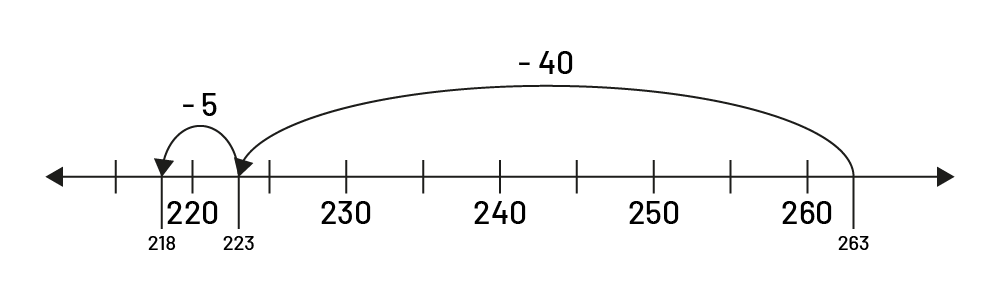
The open number line allows students to proceed in significant leaps \((263\; - \;3\; = \;260,\;260\; - \;40\; = \;220,\;220\; - \;2\; = \;218)\):

Students can use drawings to quickly illustrate a numerical expression such as \(1\;369\; - \,821\). Numbers can be represented by lines, circles, dots, and so on. A separation or removal can be expressed as hatch marks on the drawing. For 1369, you need to remove 8 hundreds, 2 tens and 1 one from 13 hundreds, 6 tens and 9 ones.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 127-129.
Skill: Representing and Solving Problems Involving Addition and Subtraction of Decimal Tenths
The student will use prior knowledge of whole numbers to solve problems involving decimal numbers and will use the same types of student-generated algorithms, since they are based on the meaning of the number rather than the position of the digits. As a result, the student will be able to clearly explain the meaning of the computations performed.
Source: translated from Les mathématiques...un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure 6e, module 3, série 2, p. 179
Example
Sophie is making two necklaces with beads.
She uses 1.5 m of yarn to make the first and 2.7 m of yarn to make the second. What length of yarn did she use in total?
To add decimal numbers effectively, students need to understand the place value of the digits that make up each number and factor this into their calculations. Students must also recognize that the decimal point is a marker that identifies the place value of the digits. When adding, to ensure that the place values match, the decimal points can be aligned. For students who have a good sense of addition and place value, aligning the decimal point is not a rule to be memorized, but a way to account for place values.
When adding decimal numbers, the concept of grouping is used just as when adding whole numbers. For example, 7 tenths can be added to 5 tenths to get 12 tenths. Since the decimal system does not allow two digits to be placed in the same position, students need to understand the concept of regrouping.
5 tenths + 7 tenths = 12 tenths
(The rod  represents one unit)
represents one unit)

The decimal system does not allow two digits to be in the same position.

Since 10 tenths can be grouped into 1 ont (unit), we have 1 unit and 2 tenths.

The quantity "12 tenths" is written 1.2.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 98-99.
The base ten blocks and the place value mat are a great support to developing conceptual understanding of adding and subtracting decimals. With these materials, quantities of the same value are joined together explicitly, for example, tenths are added with tenths. When students work with base ten blocks, they use their knowledge of place value and, in so doing, deepen the concept of grouping, transferring this concept from whole numbers to situations involving decimal numbers. Students then recognize that regardless of place value, whenever 10 elements are found in a position, they are replaced by 1 group of 10 that is placed in the position to its left. Using this type of material increases students' understanding and introduces them to algorithms for adding decimal numbers.
It is important for teachers to have students make connections between these strategies in order to consolidate addition of decimal numbers. The following are different strategies for solving the problem below:
\(1.5\; + \;2.7\)
In order to estimate the sum, it is possible to reason as follows: \(1.5\; + \;2.7\), is about \(2\; + \;3\), so about 5.
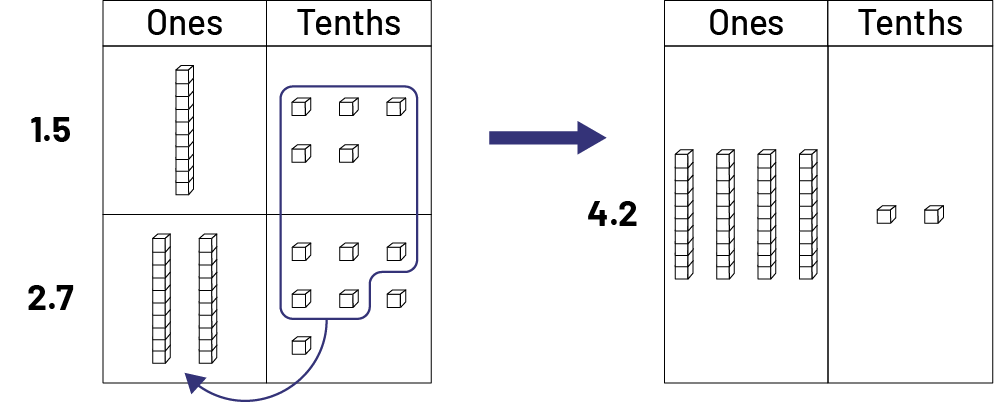
Addition Using Base Ten Blocks
To add the two quantities, each of the two numbers is represented using base ten blocks on a place value mat. By putting the material together, we obtain 3 ones and 12 tenths. We gather 10 tenths which we exchange for 1 one. We then have 4 and 2 tenths, or 4.2.
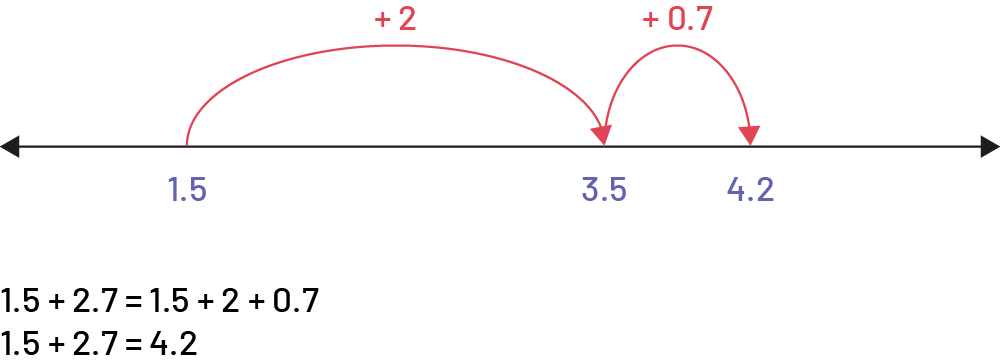
Addition Using a Number Line
The second addend is decomposed into two parts that become jumps on the number line.
\(\begin{array}{l}1.5 + 2.7 = 1.5 + 2 + 0.7\\1.5 + 2.7 = 4.2\;\;\,\end{array}\)
Addition Using Words
\(\begin{array}{l}1{\rm{\ and \ 5 \ tenths}}\;{\rm{ + }}\;{\rm{2 \ and \ 7 \ tenths}}\\{\rm{ = }}\;{\rm{3 \ and \ 12 \ tenths}}\\{\rm{ = }}\;{\rm{3}}\;{\rm{ + }}\;{\rm{1 \ and \ 2 \ tenths}}\\{\rm{ = }}\;4{\rm{ \ and \ 2 \ tenths}}\\{\rm{ = }}\;{\rm{4}}{\rm{.2}}\end{array}\)
Addition Using a Student-Generated Algorithm
The numbers are decomposed according to the place values.
\(\begin{array}{l}1.5 + 2.7\\0.5 + 0.7 = 1.2\\1 + 2 = 3\\3 + 1.2 = 4.2\end{array}\)
Student Reasoning
- 5 tenths plus 7 tenths gives 12 tenths, which is equivalent to 1 unit and 2 tenths (1.2).
- 1 plus 2 is 3.
- \(3\; + \;1.2\; = \;4.2\).
Addition Using a Standard Algorithm
\(\begin{array}{l}\;\,{}^11.5\\\underline { + 2.7} \\\;\;\,4.2\end{array}\)
Student Reasoning
- 5 tenths plus 7 tenths is 12 tenths. I exchange 10 tenths for 1. So I have 1 2 tenths. I write a 2 at the bottom in the tenths column and a small 1 at the top in the ones column to show this.
- 1 plus 1 plus 2 is 4. I write a 4 down in the ones column.
- In all, there are 4 2 tenths.
Example of Comparison
Christopher uses 3.4 m of wire to make two beaded necklaces.
Sophie uses 1.2 m of thread to make two beaded bracelets.
How much more thread does Christopher use than Sophie?
During subtraction, it is important, as it was for addition, to consider the place value of the digits that make up the numbers. The strategies for subtracting decimal numbers are essentially the same as those used for subtracting whole numbers.
Subtraction Using Base Ten Materials
When using concrete materials to represent subtraction, students can actually manipulate quantities. To determine a difference, students can compare one quantity to another or take one quantity away from another. In addition, students discover, through the use of these materials, that sometimes exchanges are necessary to make it easier to determine the difference between quantities.
Source: translated frpom Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 101
\(3.4\; - \;1.2\; = \;?\)
Each number is represented using base ten materials and similar quantities (in red) are matched in each position. The difference is represented by the remaining quantities in the number 3.4 (in blue). Thus, we obtain \(3.4 - \;1.2 = \;2.2\).
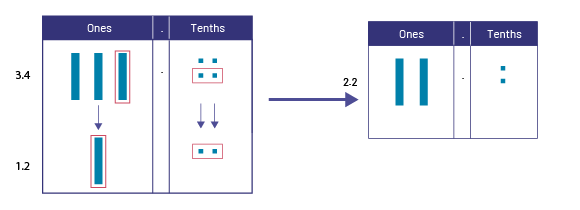
Christopher uses 2.2 m more than Sophie.
Example with Separating
Christopher uses 3.4 m of wire to make two beaded necklaces. He uses 1.2 m of wire to make the first necklace. How much wire will he use to make the second necklace?
\(3.4\; - \;1.2\; = \;?\)
Subtraction Using Base Ten Materials
The number 3.4 is represented using base ten material. Then, the equivalent of the number 1.2 is removed. The difference between the two numbers, 2.2, remains on the mat.
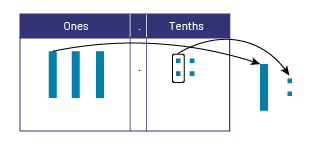
The wire used for the second necklace measures 2.2 m.
Example of Regrouping
Ahmed wants to make necklaces too. He had 2.4 m of wire. He uses 1.6 m for the first necklace. How much wire will he use to make the second necklace?
\[2.4 - 1.6 = ?\]
Subtraction Using Base Ten Materials
The number 2.4 is represented using base ten materials. When we try to use the separating strategy to perform the subtraction, we realize that there are only 4 tenths on the mat and we need to take away 6 tenths. In this case, we separate 1 one or rod into 10 tenths. We then remove the equivalent of the number 1.6.

The difference between the two numbers, 0.8, remains on the mat.
So the length of wire used to make the second necklace is 0.8 m.
Subtraction Using a Number Line

Subtraction Using a Student-Generated Algorithm
\(\begin{align}2.&4\; - \;1.6\\2.4\; - \;\left( {1.4\; + \;0.2} \right)\\2.&4\; - \;1.4 = \;1\\ &1\; - \;0.2 = \;0.8\end{align}\)
Student Reasoning
I decomposed the second number and then removed the parts according to the place values.
So the length of wire used to make the second necklace is 0.8 m.
Subtraction Using a Standard Algorithm
The standard algorithm also allows subtraction with decimal numbers. However, you have to make sure to match the place values.

Student Reasoning
- It is impossible to remove 6 tenths from 4 tenths, so I regrouped 1 one into 10 tenths. Then I had 1 and 14 tenths.
- 14 tenths minus 6 tenths is 8 tenths.
- In the ones column, I have 1 minus 1 is 0.
So the length of wire used to make the second necklace is 0.8 m.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 99-104.
Particular attention should be paid to subtraction involving numbers with a 0 in the ones or tens position. Van de Walle and Folk (2005, p. 193) suggest that it is most effective to address this issue when students are working with manipulatives. It is important to give students the opportunity to discuss the different strategies used to perform subtraction with such numbers.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 59.
Knowledge: Algorithm
Algorithms are sets of rules and ordered actions needed to add, subtract, multiply or divide. In simple terms, an algorithm is the "recipe" for an operation. (Kilpatrick, Swafford and Findell, 2001, p. 103)
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 75.
Knowledge: Student-Generated Algorithm
A strategy, usually developed by the student, for carrying out a computation.
Example

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 76.
