B2.6 Represent and solve problems involving the division of two- or three-digit whole numbers by one-digit whole numbers, expressing the remainder as a fraction when appropriate, using appropriate tools, including arrays.
Skill: Solving Problems Involving Division of Two- or Three-Digit Whole Numbers by One-Digit Whole Numbers
Students develop an understanding of multiplication and division and the relationships between numbers by solving written problems. The types of problems presented below with examples can help students see the basic multiplication and division facts in a variety of ways, depending on whether the problems are equal group, multiplicative comparison, or combination problems. Using problems to introduce basic number facts forces students to reason their way to solutions and thus develops a better sense of operations.
Equal-Grouping: Number of Groups Unknown
The school has purchased 150 books for the classrooms and is preparing bins. A parent volunteer puts 30 books in each bin. How many bins did the parent use?
\[150 \div 30 = ?\;{\rm{or}}\;?\; \times 30 = 150\]
The Array
The parent volunteer used 5 bins for books.
Equal-Sharing: Group Size Unknown
The school purchases 150 books for each of the 5 classes. A parent volunteer prepares 5 bins of books. How many books are in each bin?
\[150 \div 5 = ?\;{\rm{ou}}\;5\; \times ? = 150\]
Sharing (Partitive)
\[10 + 10 + 10 = 30\]
Each bin holds 30 books.
Combination Problem
Combination: Size of Set Unknown
Mustapha has new shirts and pants. He has 15 different outfits in all. If he has three pairs of pants, how many shirts does Mustapha have?
\[15 \div 3 = ?\;{\rm{ou}}\;3\; \times ? = 15\]
Equal-Sharing - Tree Diagram
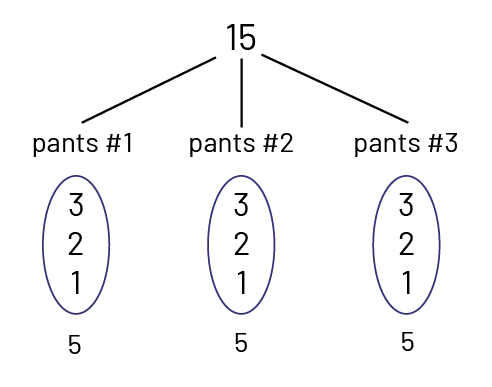
\[15 \div 3 = 5\;{\rm{ou}}\;3\; \times 5 = 15\]
Mustapha has 5 shirts.
Source: Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10-11.
The concept of remainder
In a division, the concept of a remainder arises when the quotient is not a whole number. For example, \(10\; \div \;3\; = \;3\;{\rm{ with \;1 \; remainder \; or\; 3}} \frac{1}{3}\) . For many students, the remainder is just a number that appears in the "recipe" for division (for example, \(123\; \div \;5\; = \;24\;{\rm{with \; a \; remainder\; of }}\;{\rm{3}}\)).
However, when the operation arises from a context, the remainder must be considered in order to adequately address the problem. Thus, students can develop the ability to deal with the remainder if they are in a problem-solving situation.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 87.
It is recommended that students be exposed to divisions with a remainder from a young age, since in everyday life, the divisions we make are not always round numbers. It is important to introduce these divisions in a context related to students' experiences, as it is an abstract concept.
Example
- Without Context
\(10\; \div \;3\; = \;3{\rm{R1}}\)
What does R1 represent, a child or a candy?
- With Context
In the following example, the remainder is distributed equally and expressed as a fraction.
Lucas wants to give 10 muffins to his 3 friends. He wants each friend to receive the same amount of muffins. How many muffins does he give to each of his 3 friends?
In context, it is easier to determine what the R1 represents. Here, it is a muffin.
Each child will have \(3\; + \;\frac{1}{3}\) muffins or \(3\frac{1}{3}\).
The remainder is expressed as a fraction, since a muffin can be divided.
Source: L'@telier - Ressources pédagogiques en ligne (atelier.on.ca),
Computational Strategies
The following are a variety of strategies that can be used to carry out a division. They answer to a variety of needs and facilitate student learning.
To make this section easier to read and understand, the operations are presented as numerical expressions and models. In the classroom, teachers should also represent the computations horizontally, for example: \(432 \div 5\).
When faced with a division to be carried out, either one looks for the number of groups - quotative division - or one looks for the size of each group - partative division. Thus, computational strategies may differ depending on the type of division. Students should have the opportunity to learn and use multiple strategies to solve division problems of both types.
As with other operations, students may initially use manipulatives.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 121, 140-145.
Example 1
Mrs. Langlois has 125 stickers. Every day, she gives 5 stickers to students. After how many days will Mrs. Langlois have given all her stickers?
\[125 \div 5 = ?\]
Estimation
\(\begin{array}{c}125 \div 5 \approx 100 \div 5\\ \approx 20\end{array}\)
Strategy 1
Division Using an Array
I decompose 125 into \(100\; + \;25\), which are 2 multiples of 5. This makes division easier.
I first divide 100 by 5 and then 25 by 5. I add the two quotients to get the number of days for Mrs. Langlois to give all her stickers.
\(20\; + \;5\; = \;25\)
They will then be able to conclude that Mrs. Langlois will be able to give out stickers for 25 days.
Strategy 2
Division Using the Double Number Line
I decompose 125 into \(100\; + \;25\), which are 2 multiples of 5. This makes division easier.
\(\begin{array}{l}100 \div 5 = 20\\25 \div 5 = 5\\20 + 5 = 25\end{array}\)
They will then be able to conclude that Mrs. Langlois will be able to give out stickers for 25 days.
Example 2
At Aureste School, the principal buys 252 packages of grid-paper. She divides them equally among 8 classes. How many packages does each class receive?
\[252 \div 8 = ?\]
Estimation
\(\begin{array}{c}252 \div 8 \approx 240 \div 8\approx 30\end{array}\)
I know my answer is about 30 packages.
Strategy 1
Division Using an Array
I decompose 252 into the multiples of 8 that I know, that is, \(80 + \;80 + \;80\) and I am left with 12.
I know that \(80\; \div \;8\; = \;10\). There are 12 left. So I can make another group of 8. I have 4 packages left. I can divide each package into 2 to make 8 half packages.
\(\ 10 + 10 + 10 + 1 + \frac{1}{2} = 31\frac{1}{2}\)
She distributes \(\ 31\frac{1}{2}\) packages to each class.
Source: adapted from Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 4e année, Module 2, Série 2, Introduction, p. 172.
Strategy 2
Division Using Multiplication
I decompose 252 into the multiples of 8 that I know, that is, \(80 + \;80; + \;80\) and I am left with 12.
I multiply \(8 \times 10\), 3 times. I add the partial products. I subtract 240 from 252, which gives me 12. I multiply 8 x 1, so I can distribute 31 packages per class and have 4 packages left over.
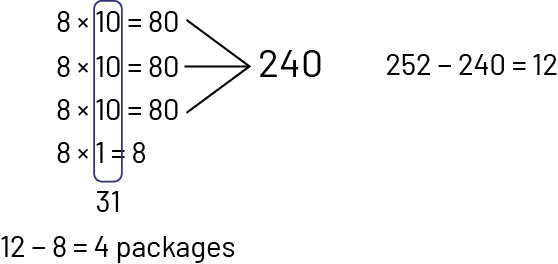
There are 4 packages left. I can divide each package into 2 to have 8 half-packages.
She then distributes \(31\frac{1}{2}\) packages to each class.
Source: adapted from Les mathématiques... un peu, beaucoup, à la folie, Guide pédagogique, Numération et sens du nombre/Mesure, 4e année, Module 2, Série 2, Introduction, p. 172.
Knowledge: Types of Division
There are two types of division problems. The others are derived from multiplication.
The "Equal-Grouping" Division
Here we know the total number and the size of each group. We are looking for the number of groups.
The "Equal-Sharing" Division
Here, a set of objects is divided equally among a number of groups or individuals. We know the total number and the number of groups. We look for the number of objects in each group or the size of each group.