B1.4 Represent fractions from halves to tenths using drawings, tools, and standard fractional notation, and explain the meanings of the denominator and the numerator.
Activity 1: From Smallest to Largest
Relationship Skills
Make connections between the number of wholes (numerator) and the number of partitions the whole is being divided into (denominator).
Directions
Hand out a random list of unit fractions (for example, \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{5}\), \(\frac{1}{7}\), \(\frac{1}{8}\), \(\frac{1}{9}\), and \(\frac{1}{10}\).
Have students place them in ascending order using manipulatives.
Ask them to explain their sequence and justify it.
Note: Represent these fractions with concrete materials by using all four models: length model, surface model, volume model and overall model. It is important for students to know what each fraction represents based on the models and to be able to tell which fraction is greater.
Intervention
Circulate and ask questions such as:
- Which fraction is larger? Smaller? How do you know?
- What does each number in a fraction represent?
- What is different between the objects you used to represent your fractions and those of others? What is the same?
Source: Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 68-69.
Activity 2: Let's Take Pictures of Fractions
Give students various statements of situations where fractions are used and ask them to represent them.
Examples
I swam three-fourths (\(\frac{3}{4}\)) of the way across the lake before I felt tired.
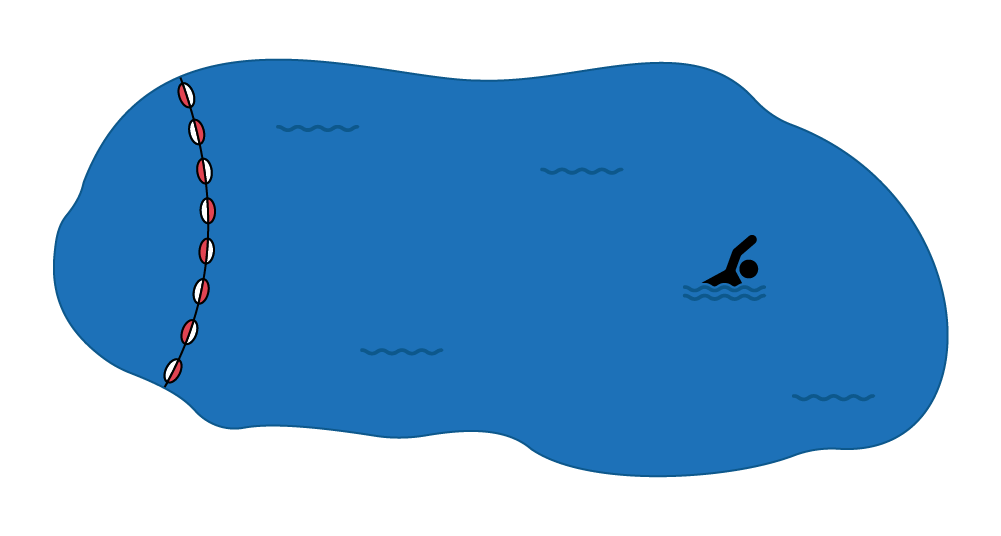
I drank a third (\(\frac{1}{3}\)) of my glass of milk.
Here are some examples of possible statements:
- I crossed three fifths (\(\frac{3}{5}\)) of the soccer field.
- Nine-tenths (\(\frac{9}{{10}}\)) of the pencils in my bag are coloured.
- Two-thirds (\(\frac{2}{3}\)) of the dozen donuts are chocolate.
- The child has not eaten even a third (\(\frac{1}{3}\)) of his plate.
- My brother is two-thirds (\(\frac{2}{3}\)) my size.
- I climbed the five eighths (\(\frac{5}{8}\)) of the ladder.
- I was two-thirds (\(\frac{2}{3}\)) of the way down the race track when he passed me.
- Nearly one-third (\(\frac{1}{3}\)) of the students in the class wear glasses.
- I spotted the squirrel when it had climbed three fourths (\(\frac{3}{4}\)) of the way up the flagpole.
- The auditorium was barely one fifth (\(\frac{1}{5}\)) filled.
- There is one fourth (\(\frac{1}{4}\)) of milk left in the glass.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 136.