B2.4 Represent and solve problems involving the addition and subtraction of whole numbers that add up to no more than 10 000 and of decimal tenths, using appropriate tools and strategies, including algorithms.
Activity 1: Sums and Differences of Whole Numbers
It is important to introduce and develop a conceptual understanding of the basic facts in a problem-solving context. This will make the numbers more meaningful to students.
Here are various questions for addition and subtraction contexts. The numbers can be adapted to respond to student needs.
- Join Problem:
At the zoo I saw 20 monkeys, 2 elephants, 14 penguins and 9 bears. How many animals did I see?
- Separate Problem (subtraction):
Amélie is so excited to see her cousin. There are only 17 days left before she arrives. How many weeks are left before she arrives?
- Separate Problem (subtraction):
Maxime has 9 bran muffins. He eats 4 of them. How many does he have left?
- Join (subtraction) problem:
Maxime wants to buy more muffins. He has $4. The muffins cost $9. How much money does he need to take out of his bank?
- Join (subtraction) problem:
John must collect 500 recyclable bottles to win a computer game. He already has 138 bottles. How many bottles does he need?
- Compare Problem (subtraction):
I have 13 books in total. There are some on my desk and there are 5 in my backpack. How many books are on my desk?
- Compare Problem (subtraction):
A train has 34 cars. Eleven of them are carrying fruit. How many cars are carrying something other than fruit?
- Separate Problem (subtraction):
Joanne had chalk. She gave 6 pieces to Francine. Now she has 9 pieces left. How many pieces did she have to begin with?
- Separate Problem (subtraction):
Marc-Andre has 43 stickers. After giving 27 to his friend Rosa, how many stickers does he have left?
- Compare Problem (subtraction):
Carla went to the orchard twice. The first time, she picked 53 apples. The second time, she picked 72 apples. How many more apples did she pick the second time?
- Join Problem and Comparing Problem:
Dora has this amount of money:

How much more money does she need to buy a yo-yo that costs $ 1.55?
- Compare Problem (subtraction):
The red team has read 674 books and the yellow team has read 328. Find out how many books the yellow team must read to have read the same number of books as the red team.
- Join Problem (addition) and Separating Problem (subtraction):
Thomas found 123 fossils. He found 456 more the next day, but lost 98. How many more does he have?
Source: translated from L'@telier - Ressources pédagogique en ligne (atelier.on.ca).
Activity 2: The Surprise Bag
Distribute to each pair of students a bag of base ten blocks (with a few flats, 10 to 20 rods, and 20 to 30 small cubes) and two place-value mats as shown below.
| Tens | Ones | . | Tenths |
|---|---|---|---|
Specify that for the activity, the rod represents one whole. The flat then represents a ten (10 rods) and the small cube represents a tenth (0.1 of a rod). Explain to the students that they must:
-
take turns to pick a quantity of base ten blocks from the bag with both hands;
-
place the blocks on the place value mat in the appropriate places;
-
make the possible groupings (for example, replace 10 small cubes by 1 rod or 10 rods by a flat);
-
calculate the sum or the difference of the two numbers.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 156.
Activity 3: Problems to Solve
- A weather station recorded the rainfall for the month of May. Here are the amounts in millimetres for the 5 days it rained that month: 1.2 mm, 0.8 mm, 2.1 mm, 8.9 mm and 4.7 mm. What is the total amount of rainfall for the month of May?
Mental Math Strategy
1.2 and 0.8 make 2
2.1 and 8.9 make 11
2 and 11 make 13
13 and 4.7 make 17.7
Thus, 17.7 mm of rain fell in May.
- A square playground has sides of 12.5 m.
- What is the perimeter of this playground?
- What is the perimeter of a playground with sides three times as long?
Student-Generated Algorithm
- \(\begin{array}{l}12.5\; + \;12.5\; = \;25\\25\; + \;25\; = \;50\end{array}\)
- \(12.5\; + \;12.5\; + \;12.5\; = \;25\; + \;12.5\; = \;37.5\)
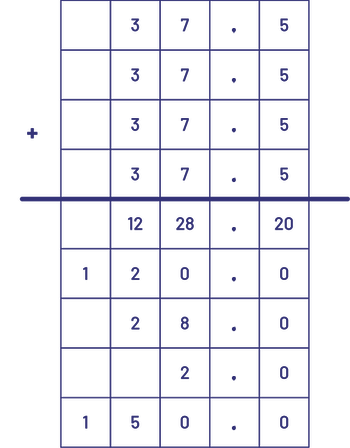
Therefore, the perimeter of the playground with sides three times the length is 150 m.
Source: adapted and translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
