B1.3 Represent equivalent fractions from halves to twelfths, including improper fractions and mixed numbers, using appropriate tools, in various contexts.
Skill: Representing Equivalent Fractions From Halves to Twelfths, Including Improper Fractions and Mixed Numbers, Using Appropriate Tools
To recognize the equality of 2 fractions is to recognize that the 2 fractions represent the same quantity. According to Van de Walle and Folk (2005, pp. 236-237), we must distinguish between the concept of equivalent fractions and the algorithm for determining equivalent fractions.
Concept: Two fractions are equivalent if they represent the same quantity.
Algorithm: To obtain a fraction equivalent to any fraction, multiply or divide its numerator and its denominator by the same number (other than 0).
The description of the algorithm presented above does not make the connection between the algorithm and the concept clear. In a classroom where the study of mathematics is based on problem solving and the use of various representations, students develop an understanding of the algorithm through the exploration of concepts. Thus, the focus is on understanding rather than on applying procedures.
The concept of equivalent fractions is introduced in Grade 1. However, it is sometimes difficult for students to grasp that a quantity can have more than one name and be represented by more than one number (for example, the number \(1\frac{2}{3}\) represents the same quantity as the number \(1\frac{6}{9}\); therefore, we say that \(1\frac{2}{3}\; = \;1\frac{6}{9}\)). Understanding equivalent fractions is part of the proportional reasoning that students will continue to develop in the intermediate and senior divisions.
Determining equivalent fractions means determining fractions that represent the same quantity. We are looking for a number of "small parts" of a whole that correspond to a particular number of "large parts" of the same whole. For example, if we are looking for the number of sixteenths that corresponds to 1 and 1 fourth (\(1\frac{1}{4}\; = \;\frac{?}{{16}}\)):
\(1\frac{1}{4}\;\) of a chocolate bar
\(1\frac{4}{{16}}\;\;{\rm{ou}}\;\frac{{20}}{{16}}\) of the same chocolate bar
Sixteenths are one fourth as large as fourths. In a whole, there are 4 fourths but 16 sixteenths, that is, 4 times more sixteenths than fourths. So you need 4 sixteenths to make a quantity that is equivalent to 1 fourth. In order to represent the same quantity, you need 4 times as many sixteenths as fourths \(\left( {4\; \times \;1\; = \;4} \right)\). This explains the algorithm below.
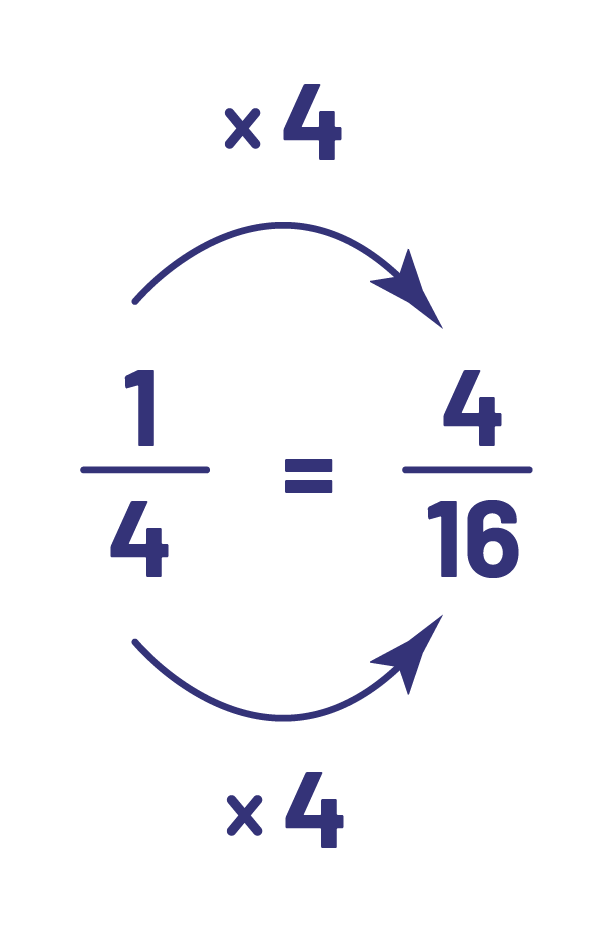
We can see that the reverse is also true. Since fourths are 4 times larger than sixteenths, \(\frac{1}{4}\) as many fourths are needed \(\left( {16\; \div \;4\; = \;4} \right)\). In order to represent the same quantity, there must be \(\frac{1}{4}\) as many sixteenths \(4 \div 4 = 1\). So, 1 fourth is equivalent to 4 sixteenths. This explains the algorithm on the right.
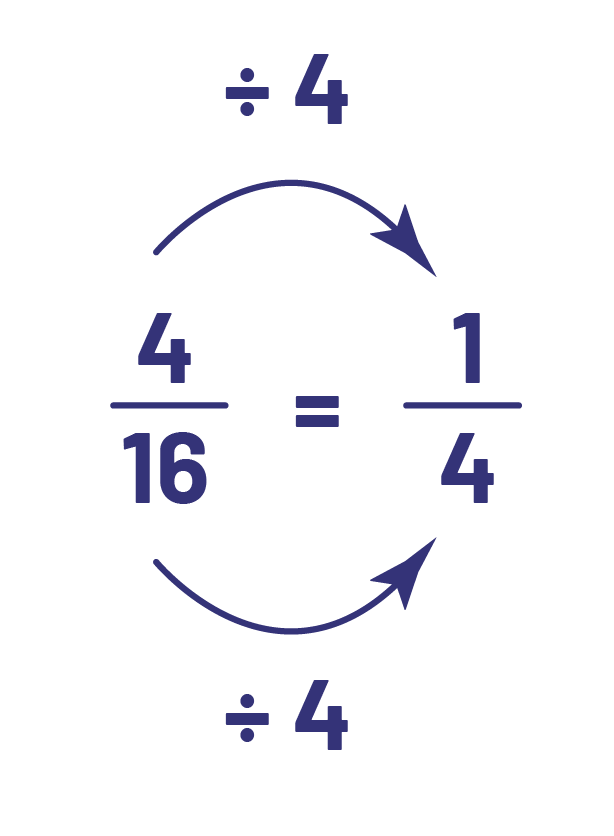
It is essential that junior students understand and can explain this relationship in order to make sense of the algorithm used to determine equivalent fractions.
However, it is not always so easy to recognize equivalent fractions. Take, for example, \(\frac{4}{6}\) and \(\frac{6}{9}\). We do not see equivalence as the result of multiplying the numerator and the denominator by an integer, which is the usual algorithm. We can reduce each fraction to its simplest expression to see that each is equivalent to \(\frac{2}{3}\). We can also use a semi-concrete representation:
\(\frac{4}{6}\)
\(\frac{6}{9}\)
This representation allows us to see the multiplicative aspect. We can see that the sixths are one and a half times bigger than the ninths. To go from the sixths to the ninths, we need 1.5 (\(1\frac{1}{2}\)) times more pieces. However, this type of situation is at a more advanced level than that expected in the junior grades.
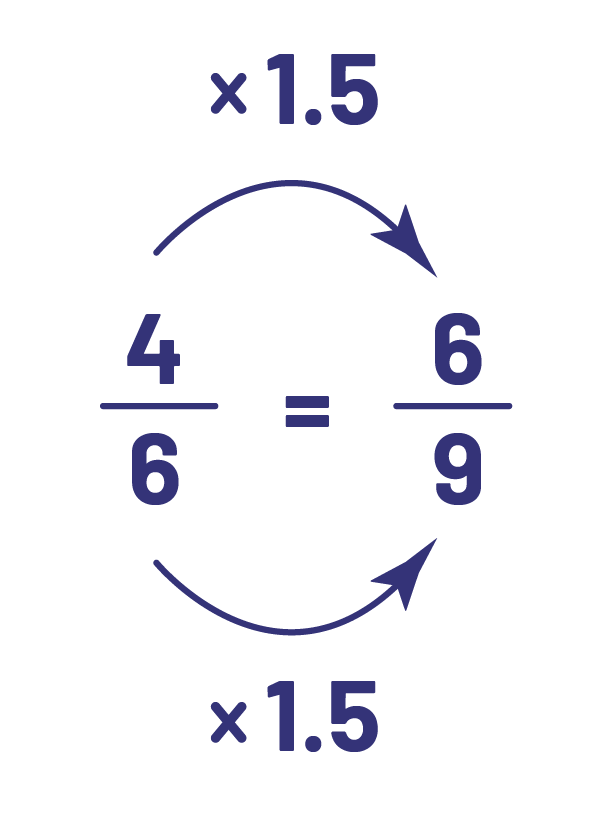
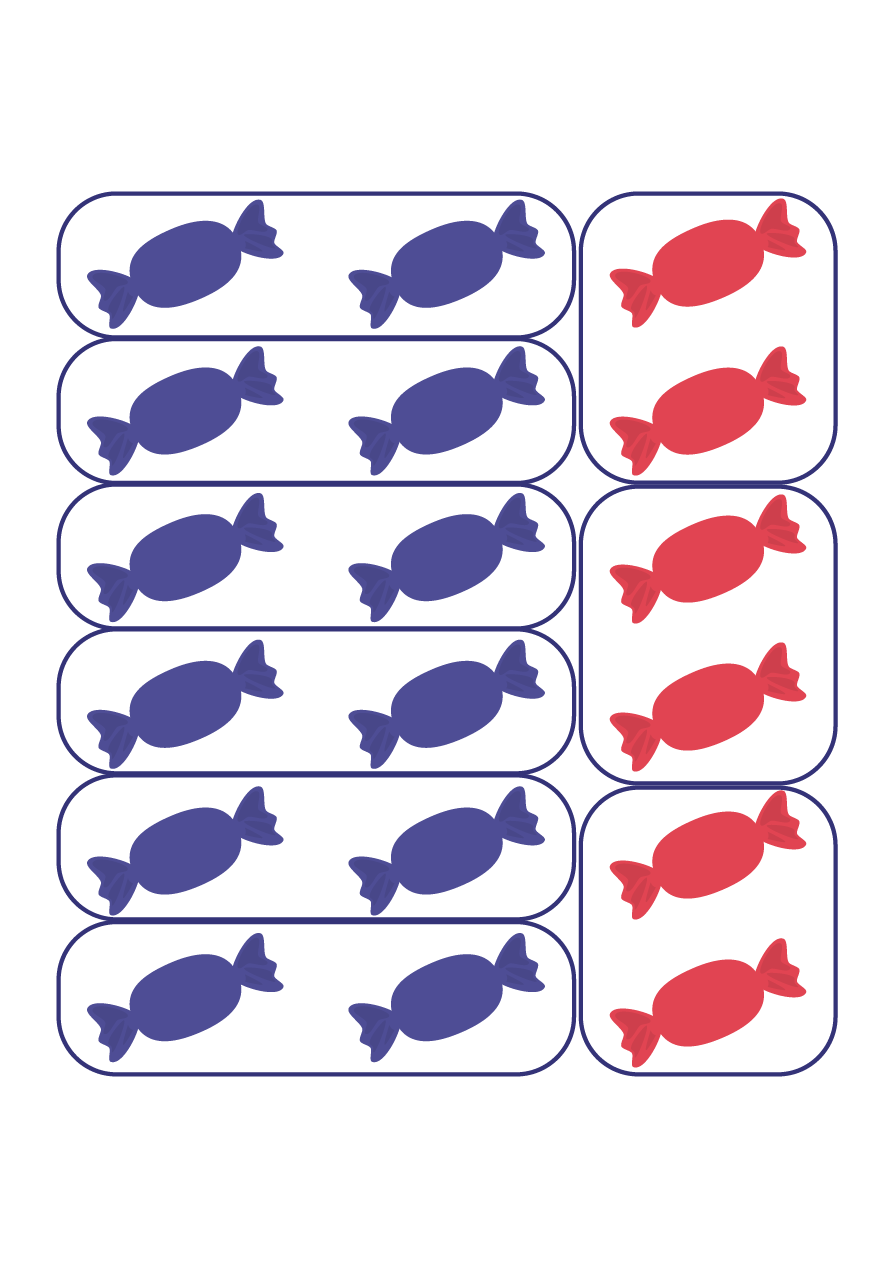
The equivalence relation must also be explored with respect to fractions of a set (the whole). In the image below, the students can easily see that \(\frac{{12}}{{18}}\) candies are wrapped in blue foil wrappers.
However, they have difficulty determining other equivalent fractions (for example, \(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{6 }{9}\)). It is therefore important to present activities that allow them to manipulate the elements of the set. Thus, students can group them into subsets of 6, 3 or 2 and determine equivalent fractions.
\(\frac{2}{3}\) candies are wrapped in blue foil
\(\frac{4}{6}\) candies are wrapped in blue foil
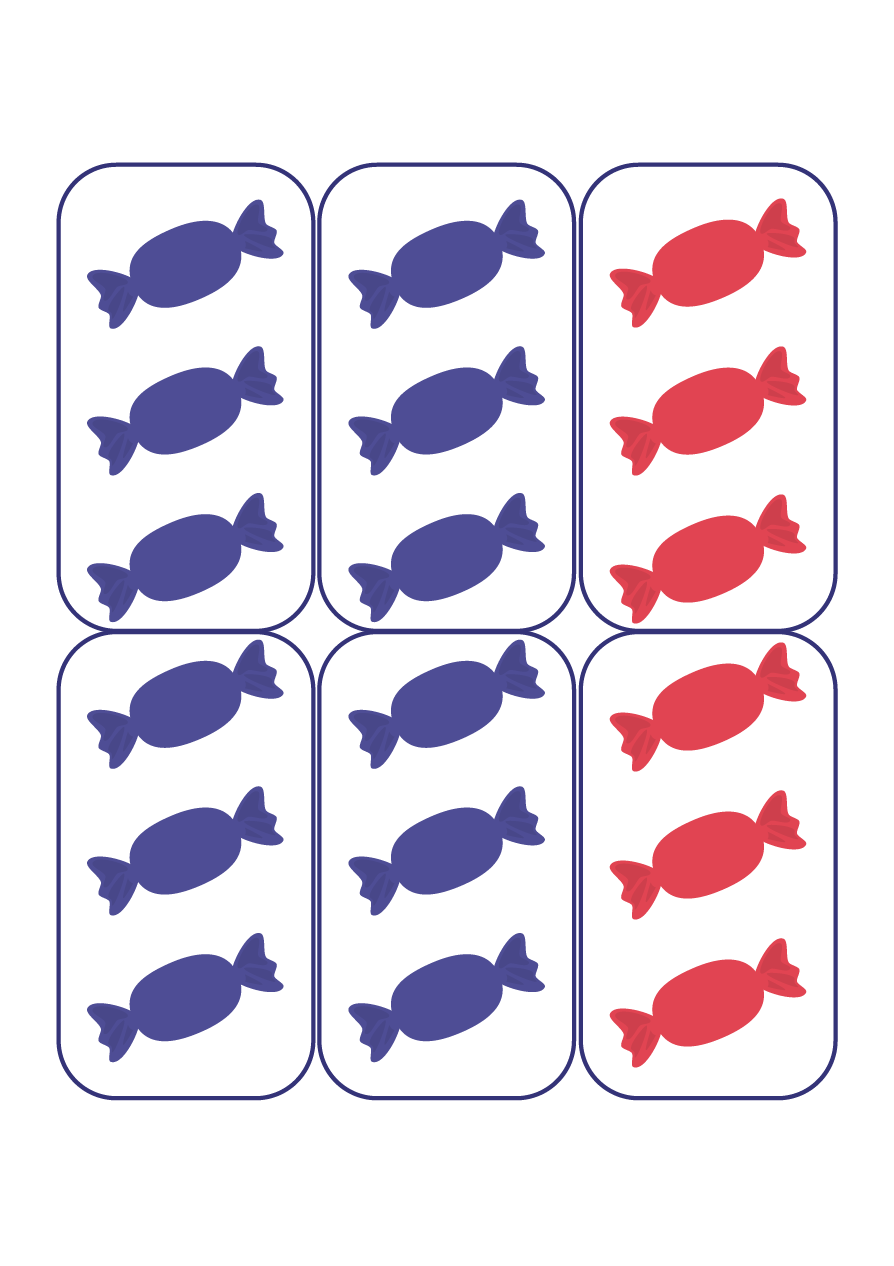
\(\frac{6}{9}\) candies are wrapped in blue foil
Concrete experience with equivalent fractions is the foundation of proportional reasoning. It cannot be overemphasized. Therefore, teachers should plan activities that build on the informal concepts related to equivalent fractions.
A few points need to be made about learning equivalent fractions. First, the focus should not be on the concept of irreducible fractions. It is better to treat these fractions like any other and to focus on equivalent fractions, that is, fractions that are different representations of the same quantity. Second, pay attention to the vocabulary that we use and the students' understanding of it, as well as the vocabulary that students use and understand. For example, some students claim that \(\frac{3}{4}\) and \(\frac{9}{12}\) are equivalent fractions, but that \(\frac{3}{4}\) is larger or smaller than \(\frac{9}{12}\) or even that it is a "better" fraction. Similarly, some students think that the fraction \(\frac{2}{3}\) is smaller than the fraction \(\frac{4}{6}\), since \(\frac{2}{3}\) was obtained when \(\frac{4}{6}\) was "reduced". It is important to determine the source of student misconceptions and to seek to correct any misconceptions.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-53.
Mixed Numbers and Improper Fractions
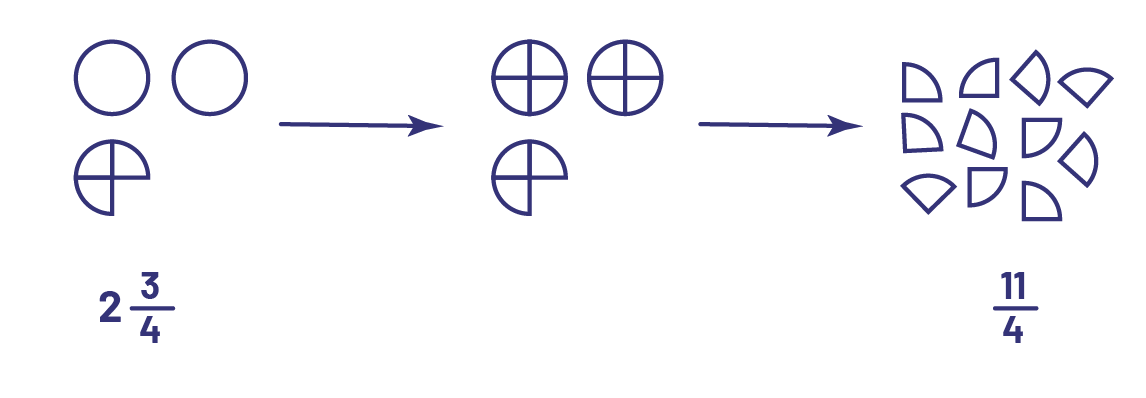
Learning fractions generally begins with the use of proper fractions, that is fractions less than 1. In the junior division, students encounter fractions that represent quantities greater than 1 (for example, if we have cut several pies into fourths, we might count 11 remaining fourths). Such situations lead them to improper fractions (for example, \(\frac{{11}}{4}\)) and mixed numbers (for example, \(2\frac{3}{4}\)).
It is important for students to recognize that a mixed number and the corresponding improper fraction represent the same quantity and that every mixed number can be expressed as an improper fraction and vice versa.
Example
If we have \(2\frac{3}{4}\) pies, we can cut each pie into fourths, making \(2\; \times \;4\), or 8 fourths. Adding the other 3 fourths gives a total of 11 fourths, or \(\frac{{11}}{4}\).
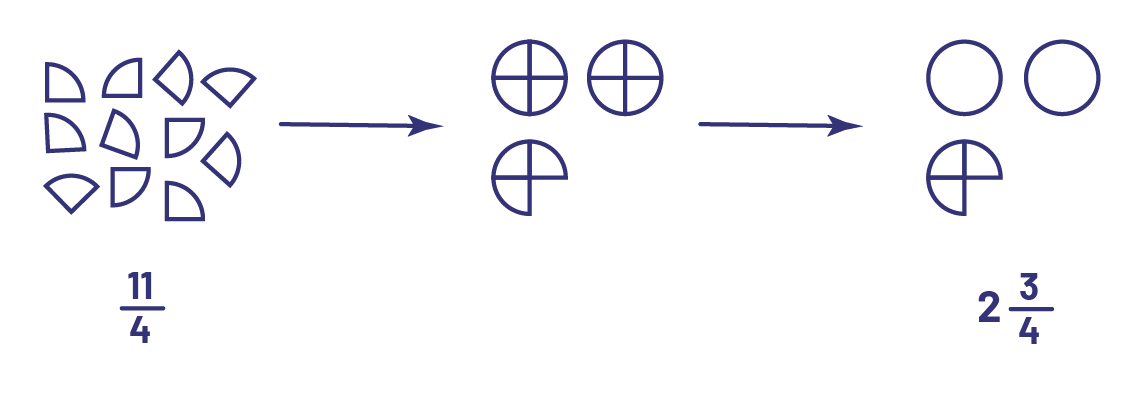
If you have 11 fourths of pie, you can group the fourths, 4 at a time, to form whole pies. This way you can form 2 pies with 8 pieces. This will leave 3 fourths. So we have \(2\frac{3}{4}\) pies.
It is important that students be able to understand the relationships between the numbers involved rather than using a prescribed procedure. This understanding can be developed by presenting activities in context and encouraging students to represent situations concretely. In this way, teachers guide students in developing their understanding.
We should take advantage of working with improper fractions to make connections with division. We know that a division, like \(5\; \div \;2\), can be expressed symbolically, by \(\frac{5}{2}\). For example, 2 children want to share 5 cookies. How many will each receive? The answer is \(2\frac{1}{2}\) cookies each. Or, we have 5 cookies that we want to put in bags, 2 per bag. How many bags will there be? The answer is \(2\frac{1}{2}\)bags (2 full bags and one half-full bag). In the 2 examples, the division of 5 by 2 (\(5\; \div \;2\)) can be expressed symbolically by \(\frac{5}{2}\) and the answer, either \(2\frac{1}{2}\), can also be expressed by \(\frac{5}{2}\). The numerical expression \(\frac{5}{2}\), in this context, therefore has 2 meanings, namely “5 divided by 2” and “5 halves”. In addition, exploration of the mixed number allows examination of the treatment of the remainder of a division. For example, if 4 friends want to share 15 bars of chocolate, how many bars will they each have? Dividing 15 by 4 (\(15\; \div \;4\)) gives a remainder of 3 which is used in the answer \(3\frac{3}{4}\).
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 53-54.
Models and tools can be used to develop understanding of equivalent fractions.
Examples
- Fraction strips or other partitioned models, such as fraction circles, can be used to create the same area as the original fraction using split or merged partitions.
- Strips of paper can be folded to show the splitting of partitions to create equivalence.
- A double number line or a ratio table can be used to show equivalent fractions based on different scales.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario, Ministry of Education, 2020.
Difficulties Encountered by Students
A fraction is a part of a whole. More abstractly, a fraction is also a number (for example, the number \(\frac{1}{2}\) could also be thought of representing half of the number 1). A fraction represents a quantity. However, this quantity is not composed only of whole number values (for example, a quantity of pears can correspond to \(\frac{1}{2}\) pear, a distance can be \(1\frac{3 }{4}\) km, that is 1 km and part of another). Fractions therefore can provide additional precision that whole numbers cannot provide.
Developing number sense related to fractions is a great challenge for students. Baroody and Coslick (1998, pp. 9-13 and 9-14) attempt an explanation and raise some difficulties in both learning and teaching fractions. The following are some of these difficulties.
- Students have difficulty picturing fractions in a variety of models. Since fractions are often taught using a single model, such as a circle or a pie, many students have not integrated the fact that in order to get a fraction, which is a part of a whole, one must first divide the whole into equivalent parts.
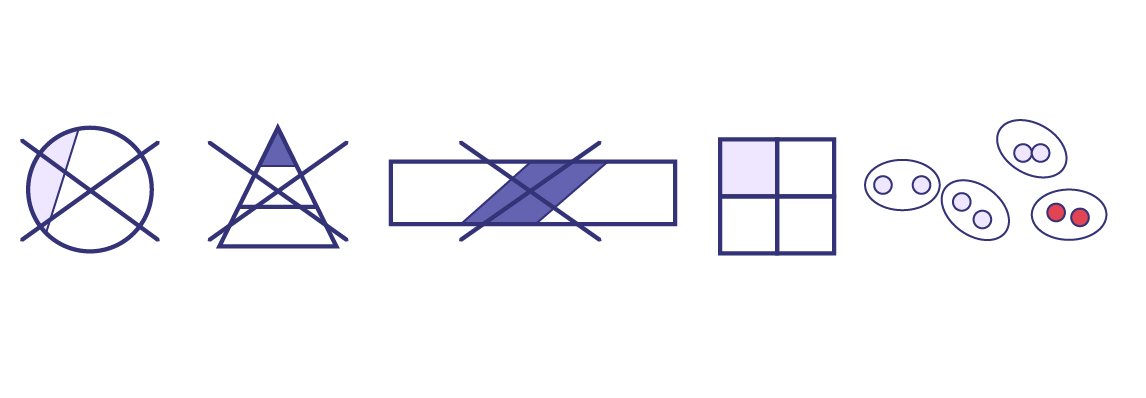
- Some students compare the part of a whole to the remaining part rather than the whole. In the following example, \(\frac{5}{8}\) of all the marbles are pink. However, some students represent this situation by the fraction \(\frac{5}{3}\).
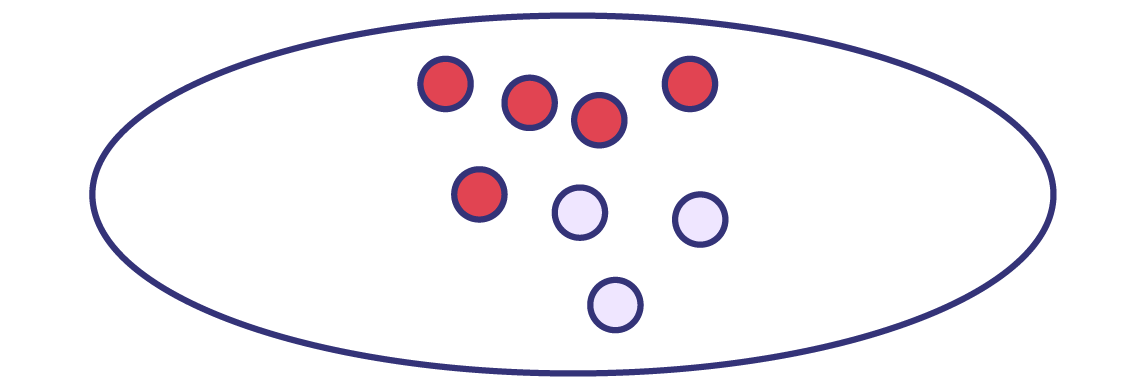
- Students do not develop a strong sense of fraction since they often do not see the connection between a fraction (for example, \(\frac{3}{4}\)) and the corresponding unit fraction (\( \frac{1}{4}\)), or that \(\frac{3}{4}\; = \;\frac{1}{4}\; + \;\frac{1}{4} \; + \;\frac{1}{4}\) or that \(\frac{3}{4}\; = \;3\; \times \;\frac{1}{4}\).
- Many students may not have mastered the concept of equivalent fractions because they do not have enough experience
to understand the multiplicative relationship that characterizes these fractions. Drawing on their past experiences
with whole numbers, they sometimes create false equivalences. For example, students write
, which is false,
instead of the equivalence 
that is true.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 29-31.
Skill: Representing Fractions in Barious Contexts
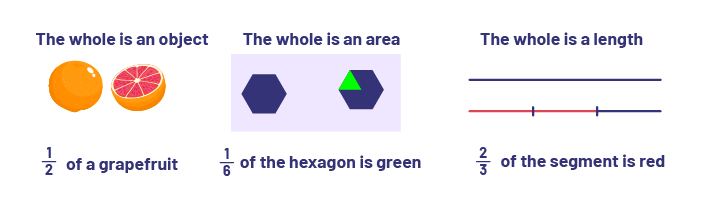
Context is all the information surrounding a situation. In the study of fractions, the whole is an essential part of the context. When solving contextual problems, a fraction such as \(\frac{2}{3}\) does not provide enough information to understand the quantity referenced without "the whole" being defined. For example, when we hear "one half", we usually think of a small quantity. However, we need to consider this quantity in context since the context may lead us to form different opinions about the same fraction. Eating half an apple at snack time is a little; eating half a pie is a lot; if half the students in the class are absent, it is a lot. As with whole numbers, context is essential for making informed decisions about the size of the quantity represented by a fraction. It is important that students learn to always consider the whole. When analysing a situation, a fraction is meaningless if it is not related to a whole. For example, we cannot compare one half of a pizza to one third of a pizza unless the two pizzas are the same size. Teachers should provide learning situations that allow students to understand that a fraction does not reveal anything about the size of the whole or its parts; it only tells us about the relationship between a whole and its parts.
In any situation, the whole corresponds to an element or a set of elements.
- If the whole corresponds to an element, it can be split into equivalent parts. Each of the parts can then be compared to the whole.
Examples
- If the whole corresponds to a set of elements, that is a collection of objects, some of the elements can be grouped together to form a part of the set and thus represent a part of the whole.
Examples
In general, when it comes to fractions, we refer to 3 different models: the set model, the linear model and the area model.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-32.
Knowledge: Equivalent Fractions
Equivalent fractions describe the same relationship or quantity.
- When working with fractions as a quotient, equivalent fractions are ones that have the same result when the numerators are divided by the denominators.
- When working with fractions as a part of a whole, the partitions of the fraction can be split or merged to create equivalent fractions. The whole remains the same size.
- When working with fractions as a comparison, the ratios between the numerator and the denominator of equivalent fractions are equal.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Knowledge: Improper Fraction
An improper fraction is one where its numerator is greater than its denominator. The fraction represents a quantity greater than one.
Examples
\(\frac{{11}}{3},\;\frac{5}{2},\;\frac{22}{{13}}\)
Knowledge: Mixed Numbers
A mixed number is a number that is composed of a whole number and a fraction; for example, 8 1/4 .
Examples
\(2\frac{1}{2},\;12\frac{2}{5},\;5\frac{{10}}{{23}}\)