B1.4 Compare and order fractions from halves to twelfths, including improper fractions and mixed numbers, in various contexts.
Skill: Comparing and Ordering Fractions From Halves to Twelfths, Including Improper Fractions and Mixed Numbers
Effective and balanced instruction enables students to develop a variety of strategies for comparing numbers. Similarly, it should enable students to develop and deepen their understanding of the meaning and value of fractions. It is through concrete experiences and representations that students learn to visualize fractions and to develop strategies for ordering, comparing, and relating them to other numbers.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 44.
To estimate a quantity, students must first understand the context by drawing on their analytical skills and their personal experiences. This often takes the form of mental images, which act as visual references. The importance of constantly enriching students' experiences to build these visual references cannot be overemphasized; they should have the opportunity to work through various situations in various contexts. It should be noted that students who have experiences working with visual models and manipulatives, such as fraction circles, counters, cardboard strips and relational rods, more easily develop a sense of magnitude, which is essential for estimating the quantity represented by a fraction.
Example
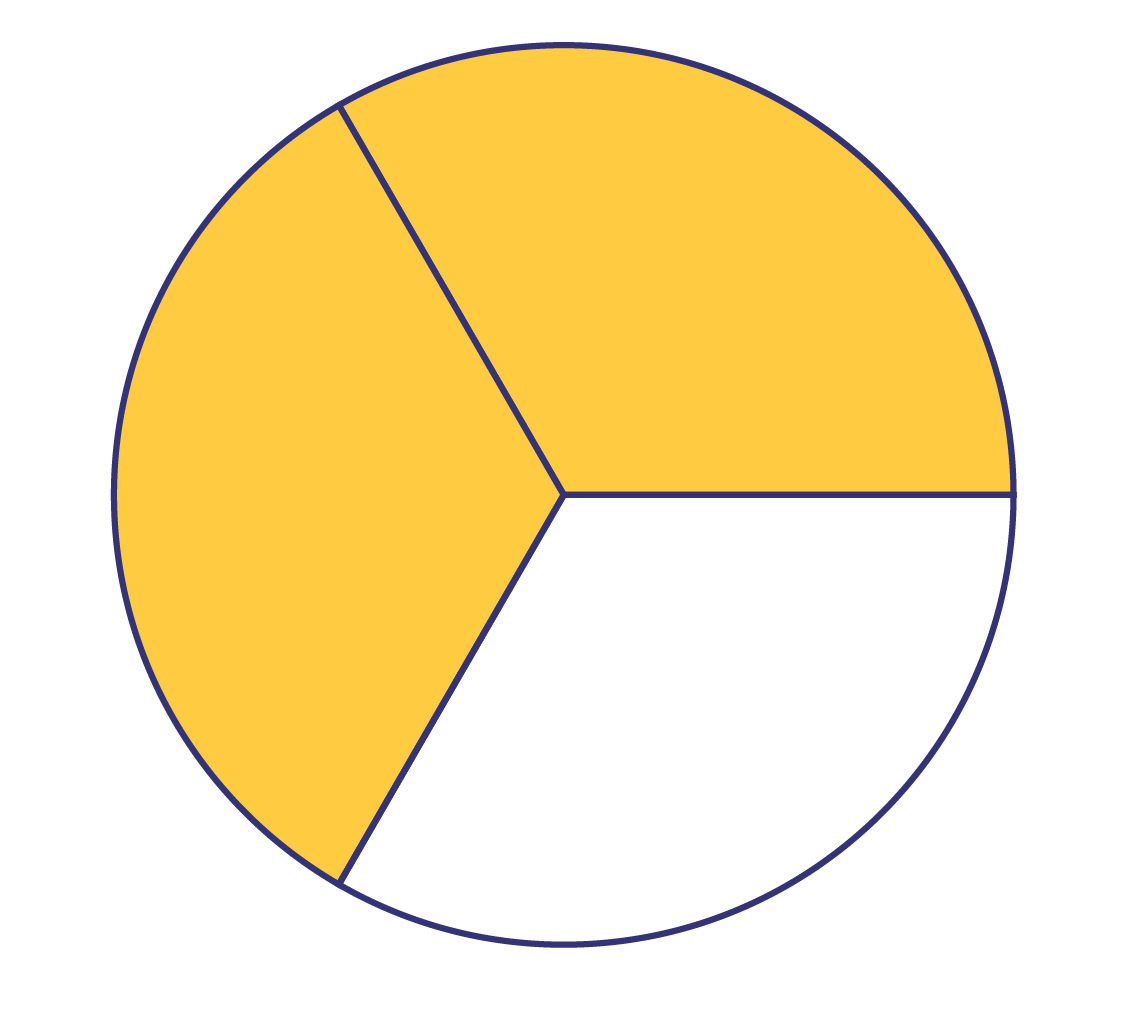
Draw the pie below and ask students to estimate the fraction of the pie that is left.

An example of student reasoning is:
- "I imagined that the pie was cut in half. I recognized that there was more than one half (\(\frac{1}{2}\)) left."

- "If it is cut into three pieces, there is less than two thirds (\(\frac{2}{3}\)) left."
- "But if it is cut into five equal pieces, I think it's very close to the size of three of those pieces."
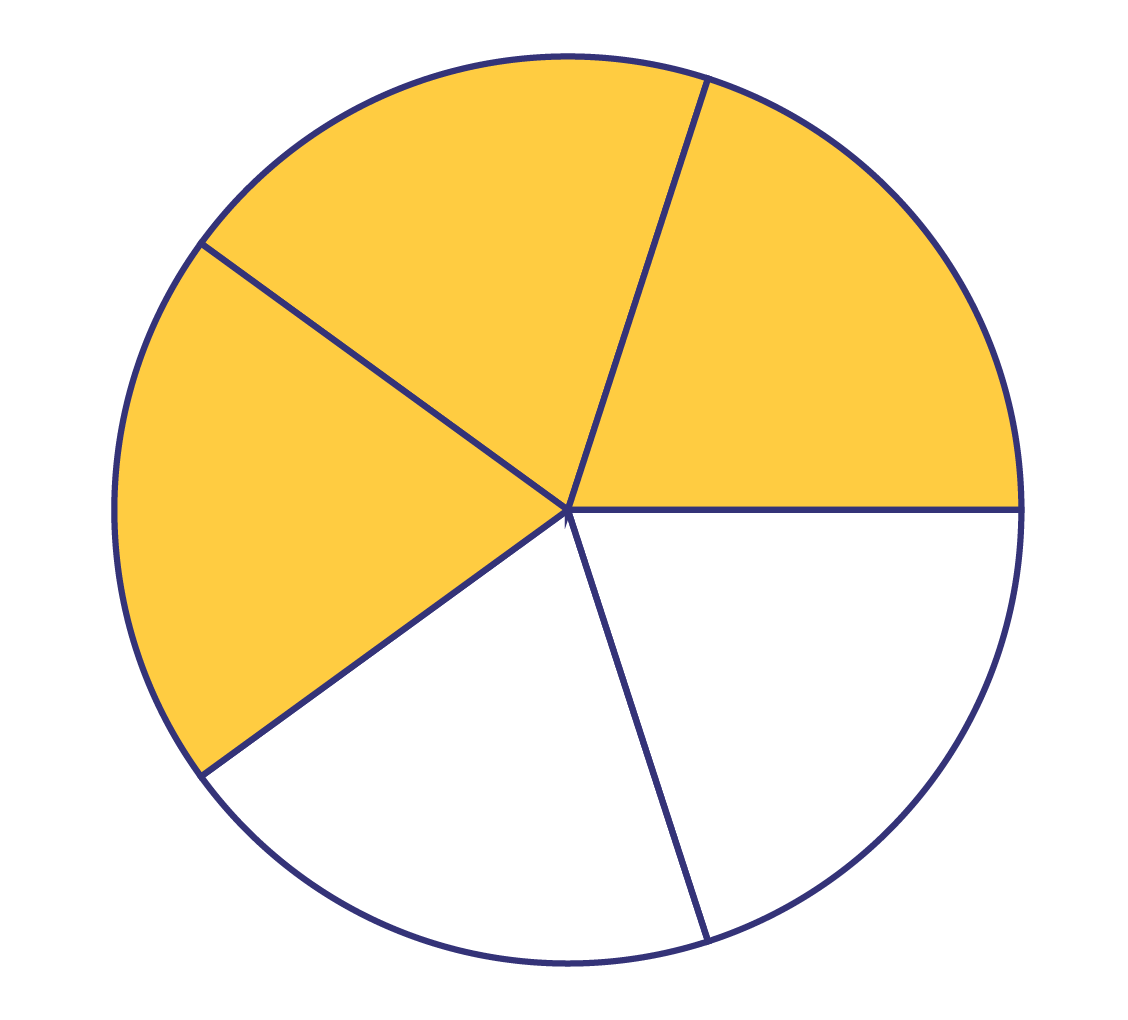
- "There is about \(\frac{3}{5}\) of the pie left."
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 38-39.
Order Relationships
It is important that students learn to order fractions by comparing them. The ability to order and the ability to compare should be based on students' constructed representations of fractions. They should arise from problem-solving situations that allow students to develop a sense of the value of a fraction and the quantity that it represents. It is this sense of the fraction that prepares students to compare two fractions and conclude that one is greater than the other. In contrast, teaching that is done out of context tends to promote learning algorithms and neglects the conceptual understanding of the fraction.
Junior students already have well-established ideas about the properties of whole numbers. However, when they begin to work with fractions, students often face a cognitive dissonance, that is to say a feeling that what was true is no longer true. For example, they learned that when it comes to whole numbers, the greater number indicates a greater quantity. They then transfer this knowledge to their work with fractions. Thus, when comparing \(\frac{1}{6}\) and \(\frac{1}{3}\), some students believe that \(\frac{1}{6}\) is greater than \(\frac{1}{3}\), since 6 is greater than 3. They feel out of balance and unsure of themselves if they are told they are wrong. To avoid such situations, learning must be based on an analytical view of the fraction rather than on memorization or an algorithm.
Activities that involve students in comparing and ordering fractions should promote the construction of fraction meaning. To compare fractions, it is rarely necessary to look for a common denominator. Thus, there are many strategies for comparing fractions. Generally, the first strategy learned is the use of a concrete or visual (semi-concrete) representation of the fractions involved. This strategy can be used on any occasion. One can also compare numerators if the denominators are the same, or compare denominators if the numerators are the same. Another effective strategy is the use of benchmark fractions.
It is important to work thoroughly on the comparison of fractions before the equivalence of fractions. This is very complex and the comparison serves as a catalyst for understanding equivalent fractions.
Comparing Fractions by Representing Them Concretely or Visually
This first strategy consists of using a model to represent the two fractions in question. For example, let's compare the fractions \(\frac{2}{5}\) and \(\frac{3}{8}\).


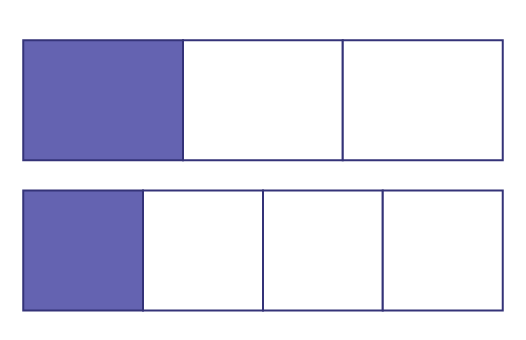
So, we can conclude by comparing the two representations that \(\frac{2}{5}\; > \;\frac{3}{8}\). It is very important to emphasize, if these fractions are of the same whole, that the same model (whole) was used to represent each of the two fractions. Students sometimes overlook the importance of the whole and misinterpret situations with fractions. For example, in the following situation, by not comparing the same whole, students could assert that \(\frac{1}{3}\; = \;\frac{1}{4}\).
\(\frac{1}{3}\)

\(\frac{1}{4}\)

In the situation shown, it is true that \(\frac{1}{3}\) of the first rectangle corresponds to \(\frac{1}{4}\) of the second rectangle. However, in order to compare fractions of the same whole, they would have had to be also represented using the same whole.
\(\frac{1}{3} > \frac{1}{4}\)
Comparing Fractions with a Common Denominator
Students generally draw on their prior knowledge and their experience with whole numbers to easily determine that \(\frac{4}{5}\) is greater than \(\frac{3}{5} \). However, the answer might not be the result of the right reasoning. Many students, for example, compare the numerators. Van de Walle and Folk (2005, p. 233) suggest that teachers emphasize that the parts are of the same size or of the same nature. Thus by comparing \(\frac{4}{5}\) and \(\frac{3}{5}\), we emphasize that \(\frac{4}{5}\) represent four parts of a certain size and that \(\frac{3}{5}\) represent three parts of this same size. We thus emphasize the comparison of elements of the same nature (fifths), as we would do if we compared three oranges and four oranges.
three fifths and four fifths of a whole

three oranges and four oranges

Comparing Fractions with a Common Numerator
In the junior grades, students are able to make sense of the numbers that make up a fraction and begin a reflective process to compare two fractions with a common numerator. For example, let's compare the fractions \(\frac{5}{9}\) and \(\frac{5}{6}\). In both cases, there are 5 parts of a whole. When the whole is divided into 9 equal parts, each part is smaller than those of the same whole divided into 6 equal parts. Thus, the ninths are smaller than the sixths and we have 5 of each in both cases. So \(\frac{5}{9}\) is smaller than \(\frac{5}{6}\).
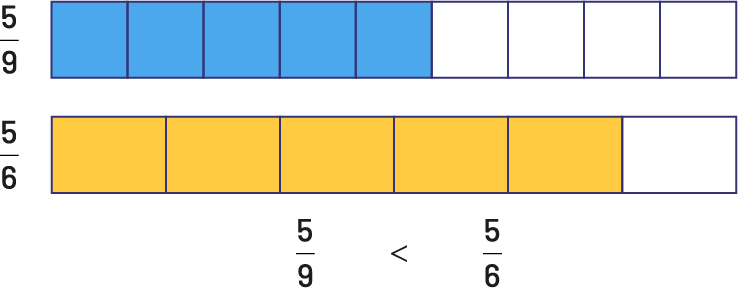
However, it is not uncommon for students to think the opposite, since 9 is larger than 6 and the numerators are the same, hence the importance of focusing on the meaning of the numerator and denominator and developing the ability to visualize fractions.
Comparing Fractions Using Benchmark Fractions
Benchmark fractions support students in developing fraction sense. Initially, students should work with three benchmarks, namely 0, \(\frac{1}{2}\) and 1. They will compare given fractions to these benchmarks.
Some generalizations that students are able to make after completing a number of learning activities with benchmark fractions are outlined in the chart below.
| \(\ 0\) | \(\frac{1}{2}\) | \(\ 1\) |
|---|---|---|
| If the denominator of a fraction is much larger than the numerator, the fraction represents a small amount, and the fraction is near 0. Thus, \(\frac{3}{{25}}\) is near 0. | If the numerator of a fraction is approximately half the denominator, the fraction is close to \(\frac{1}{2}\). Thus, \(\frac{3}{8}\) is close to \(\frac{1}{2}\). One could add that \(\frac{3}{8}\) is slightly less than \(\frac{1}{2}\), because \(\frac{3}{8}\) is less than \(\frac{4}{8}\), which is \(\frac{1}{2}\). | If the numerator of a fraction is approximately equal to the denominator, the fraction is close to 1 because it almost entirely represents the whole. Thus, \(\frac{9}{10}\) is close to 1. |
A visual (semi-concrete model) that illustrates these examples is a number line:

To compare two fractions, students can compare each to one of these benchmarks. For example, if we want to compare \(\frac{5}{{20}}\) and \(\frac{7}{8}\), we can determine that \(\frac{5}{20}\) represents a quantity between 0 and \(\frac{1}{2}\), whereas \(\frac{7}{8}\) represents a quantity between \(\frac{1}{2} \) and 1. We can therefore conclude that \(\frac{5}{{20}}\) is smaller than \(\frac{7}{8}\). Similar benchmarks can be used for mixed numbers. For example, to compare \(2\frac{5}{{20}}\) and \(2\frac{7}{8}\), we can use as benchmarks 2, \(2\frac{1}{2}\) and 3. When these benchmarks become well anchored, other benchmarks can be added, such as \(\frac{1}{4}\) and \(\frac{3}{4}\) . These benchmarks emphasize that one fourth is half of one half.
Comparing Fractions Using Other Aspects of Fraction Sense
In a problem-based learning environment, students can discover many comparison strategies based on the fraction sense they have constructed.
Example 1
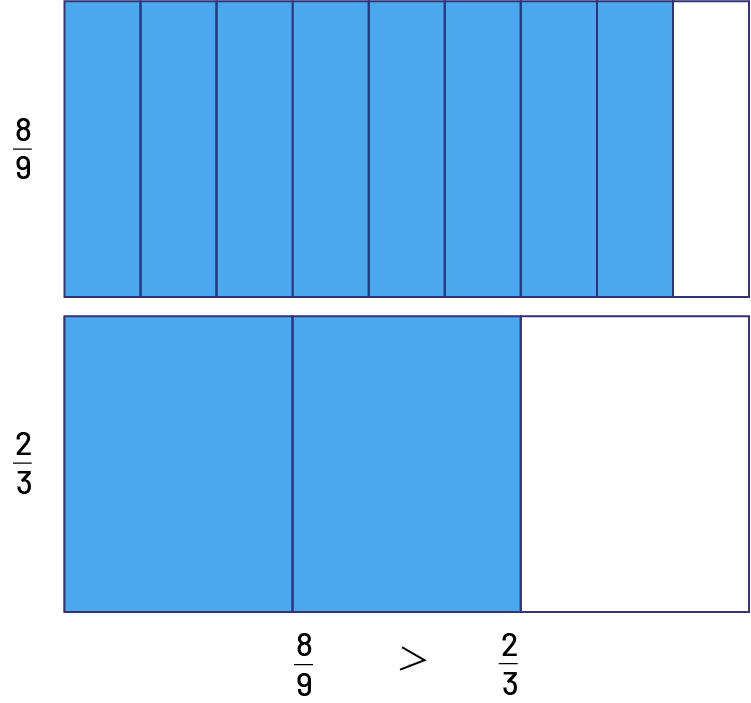
We want to compare \(\frac{8}{9}\) and \(\frac{2}{3}\). We can notice that each fraction lacks a part to make a whole. We thus recognize that for the fraction \(\frac{8}{9}\), \(\frac{1}{9}\) is missing to make 1, while for the fraction \(\frac{2} {3}\), \(\frac{1}{3}\) is missing. Since the missing part \(\frac{1}{3}\) is larger than the missing part \(\frac{1}{9}\), \(\frac{8}{9}\) is closer to 1 than \(\frac{2}{3}\). Thus, \(\frac{8}{9}\) is greater than \(\frac{2}{3}\).
Example 2
As a result of learning the various concepts related to fractions, students can use their full range of knowledge of fractions and of comparison strategies to solve problems. For example, if we want to compare \(\frac{12}{3}\) and \(\frac{17}{{12}}\). Students could use their knowledge of equivalent fractions to conclude that \(\frac{12}{3}\) is greater than \(\frac{17}{{12}}\), because \(\frac{12 }{3}\; = \;\frac{48}{{12}}\) and \(\frac{48}{{12}}\) represent more parts of the same size than \(\frac{17 }{{12}}\).
Example 3
In some car races (for example, Formula 1), the driver who crosses the finish line first wins, at which point the race is officially over. The ranking of racers is not determined by the order in which they cross the finish line as in traditional races, but rather by the position of the drivers at the end of the course, which is the fraction of the circuit they have covered when the first driver crosses the line. This system allows all drivers to be assigned a position, even those who did not finish the race.
Here is the list of fractions of the circuit covered by each driver at the end of the race:
Wagner: \(\frac{8}{9}\); Villeneuve: \(\frac{2}{3}\); Trotter: 1; Munch: \(\frac{1}{4}\); Santana: \(\frac{7}{{10}}\); Burk: \(\frac{5}{6}\); Background: \(\frac{3}{4}\); Colman: \(\frac{1}{9}\); Martina: \(\frac{5}{8}\).
Solution: Final ranking of the race
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| Trottier | Wagner | Burk | Fround | Santana | Villeneuve | Martina | Munch | Colman |
| 1 | \(\frac{8}{9}\) | \(\frac{5}{6}\) | \(\frac{3}{4}\) | \(\frac{7}{10}\) | \(\frac{2}{3}\) | \(\frac{5}{8}\) | \(\frac{1}{4}\) | \(\frac{1}{9}\) |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 44-49.
Skill: Comparing and Ordering Fractions in Various Contexts
It is important that students learn to always consider the whole. A fraction is meaningless if it is not related to a whole. For example, we cannot compare one half of a pizza and one third of another pizza if the two pizzas are not the same size. Teachers need to provide learning tasks that allow students to recognize that a fraction does not reveal anything about the size of the whole or its parts; it only tells us about the relationship between a whole and its parts.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 31.
Knowledge: Improper Fraction
An improper fraction is one where its numerator is greater than its denominator. The fraction represents a quantity greater than one.
Examples
\(\frac{{11}}{3},\;\frac{5}{2},\;\frac{22}{{13}}\)
Knowledge: Mixed Numbers
A mixed number is a number that is composed of a whole number and a fraction; for example, \(8 \frac{1}{4}\).
Examples
\(2\frac{1}{2},\;12\frac{2}{5},\;5\frac{{10}}{{23}}\)
