B1.7 Describe relationships and show equivalences among fractions, decimal numbers up to hundredths, and whole number percents, using appropriate tools and drawings, in various contexts.
Skill: Describing Relationships and Representing Equivalences Among Fractions, Decimals to Hundredths, and Percents
Students should be able to create a mental representation of a percent, as they do with decimal numbers. The very nature of a percent makes it easier for them to visualize a quantity, as it is always a ratio to 100. It should also be understood that a percent is another way of representing a quantity.
Example
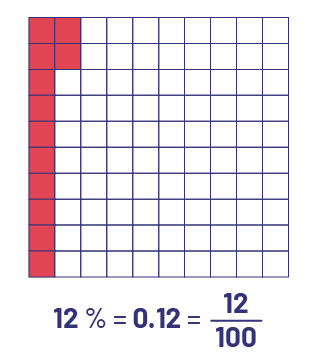
Benchmarks
The mental representations used by students are reinforced by the use of benchmarks. In general, a benchmark is a reference. The benchmarks for decimals and percents are similar to those used for fractions. By making connections between decimals, percents, and fraction benchmarks, students deepen their number sense.
The following table provides some benchmarks that students should know.
Benchmarks for Fractions, Percents and Decimals
| Fraction | Percent | Decimal Number | Example of a Mental Representation |
|---|---|---|---|
| \(\frac{1}{{10}}\) | 10% | 0.1 |  |
| \(\frac{1}{4}\) | 25% | 0.25 | 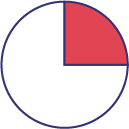 |
| \(\frac{1}{3}\) | \( \approx \;33\;\% \) | \( \approx \;0.33\ \) |  |
| \(\frac{1}{2}\) | 50% | 0.5 |  |
| \(\frac{2}{3}\) | \( \approx \;67\% \) | \( \approx \;0.67\) | 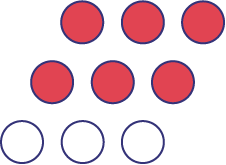 |
| \(\frac{3}{4}\) | 75% | 0.75 |  |
| 1 | 100% | 1.00 |  |
These benchmarks, as well as the relationships between fractions, percents and decimals, promote the development of number sense and are very useful in problem-solving situations. The ability to switch from one representation to another is advantageous, because it allows students to use the one that best meets the needs of the moment. For example, a customer who wants to calculate a 50% discount on the price of an item can easily do so if he recognizes that 50% is half (\(\frac{1}{2}\)).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 37-40.
Equivalence and Equality Relationships
It is important to recognize equivalencies between various representations of numbers or numerical expressions. In the context of decimal numbers, students should recognize the equality between a decimal number, the corresponding decimal fraction, and the percent.
Students need to understand that since decimal notation is just another way of representing a decimal fraction, it is then possible to establish an equality relationship between the two notations (for example, \(0.3\; = \;\frac{3}{{10}}\)). By recognizing this equality, students are better able to associate a place value with each of the digits (for example, ones, tenths, hundredths) that make up a decimal number.
Example
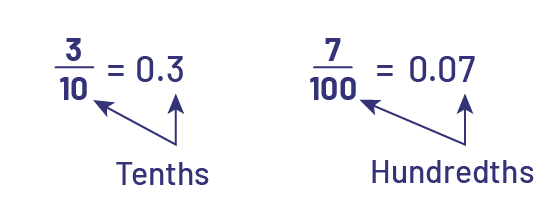
Students who do not understand this association are sometimes inclined to represent a fraction such as \(\frac{2}{5}\) by 0.2 or 0.25. The following description describes observable behaviours of students who have developed a conceptual understanding of numbers and the relationship between their different representations.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 46.
Conceptual Understanding of Numbers
Number: 0.3
Observable behaviours:
- The student reads it as three tenths.
- The student can write the number as a fraction as \(\frac{3}{{10}}\).
- The student can represent the number using concrete materials or visuals.
Example
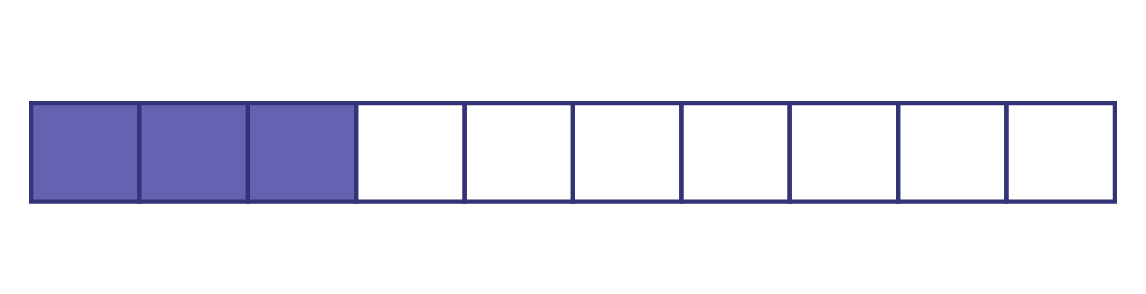
Number: \(\frac{{16}}{{100}}\)
Observable behaviours:
- The student reads it as six hundredths.
- The student can write the number in decimal notation as 0.16.
- The student can represent the number using concrete materials or visuals.
Example
Number: \(\frac{2}{7}\)
Observable behaviours:
- The student reads it as two sevenths.
- The student knows that the fraction \(\frac{2}{7}\) is not represented by 0.2 since they know that 0.2 = \(\frac{2}{10}\).
To establish the relation of equality between a fraction whose denominator is not a power of 10 (for example, \(\frac{1}{4}\)) and the corresponding decimal number, we need the concept of equivalent fractions. For example, students can use strips of equal length as shown below to see that \(\frac{1}{4}\) is between \(\frac{2}{{10}}\) and \(\frac{3}{{10}}\).

They can then subdivide the tenths into 10 equal parts, creating 100 equal parts, or hundredths of the whole, and recognize that \(\frac{{25}}{{100}}\) is a fraction equivalent to \( \frac{1}{4}\).

Since \(\frac{{25}}{{100}}\; = \;0.25\), they can conclude that the fraction \(\frac{1}{4}\) can also be represented as 0.25 (\(\frac{1}{4}\; = \;\frac{{25}}{{100}}\; = \;0.25\)). This kind of example allows students to recognize that all fractions that can be expressed by an equivalent decimal fraction can be represented by a decimal number. This is particularly the case for fractions expressed in halves, fourths, fifths and twentieths, as shown in the following table.
| Fraction | Equivalent Decimal Fraction | Decimal Number |
|---|---|---|
| \(\frac{1}{2}\) | \(\frac{5}{{10}}\) | 0.5 |
| \(\frac{3}{4}\) | \(\frac{{75}}{{100}}\) | 0.75 |
| \(\frac{2}{5}\) | \(\frac{4}{{10}}\) | 0.4 |
| \(\frac{7}{{20}}\) | \(\frac{{35}}{{100}}\) | 0.35 |
Note: Some fractions (for example, \(\frac{2}{3}\), \(\frac{3}{7}\), \(\frac{5}{{11}}\)) cannot can be represented by an equivalent decimal fraction.
Source: adapted and translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 47-48.
In Grade 5, students are not expected to work with these types of decimal numbers. They are expected to work with terminating decimals, which are fractions with denominators that are power of 10 (for example, \(0.3\; = \frac{3}{{10}}\;\); \(0.47 \;= \frac{{47}}{{100}}\;\)). Because the concept of percent is closely connected to the concept of fraction, there is only one more step to connect the percent with the decimal number and the decimal fraction. At the end of the junior grades, students who have acquired a good sense of number can move from one representation to another without difficulty.
Example
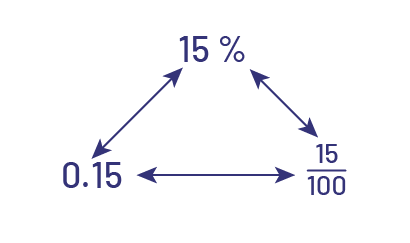
To help students develop this skill, they should be regularly invited to express their answers using another notation. For example, teachers can encourage the student who answered that \(\frac{3}{4}\) of the young people in the class have black hair to also express this answer in decimal notation (0.75) and as a percentage (75%).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 50-51.
Knowledge: Percent
Percent is a kind of a fraction. It is often used in everyday life. A numerical expression such as 30% (which reads "30 percent") is actually another representation of the number 30 hundredths, or 0.30. To facilitate understanding of the concept of percent, students should first make the connection between percent and a fraction with a denominator of 100, using concrete or visual (semi-concrete) materials.
Example

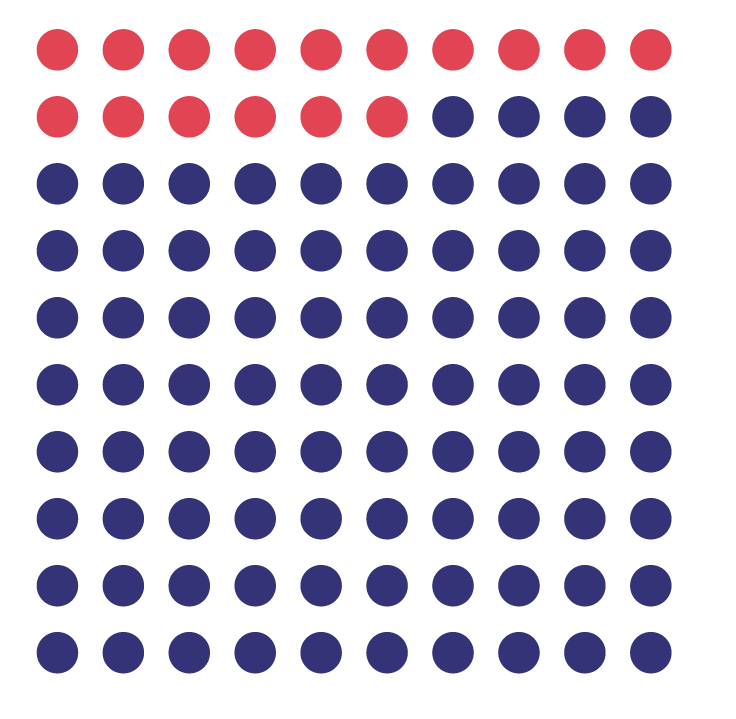
Students should also realize that a percent represents a ratio to 100 (for example, 30% represents the ratio 30:100). It is important to note that a result expressed as a percent does not mean that the quantity in question is necessarily composed of 100 parts, as explained in the following table.
Relationship Between Percent and the Quantity 100
| Representation | Percent | Instructional Notes |
|---|---|---|
  |
75% of the circles are red. | Even if 75% of the circles are red, that does not mean there are 100 circles in the whole. However, if there were 100 circles, there would be 75 red circles. Also, the fraction of circles that are red is equivalent to \(\frac{{75}}{{100}}\)(for example, \(\frac{3}{4}\; = \;\frac {{75}}{{100}}\) and if this amount were doubled, the corresponding fraction would be \(\frac{{150}}{{200}}\; = \;\frac{{75}}{{100}}\)). |
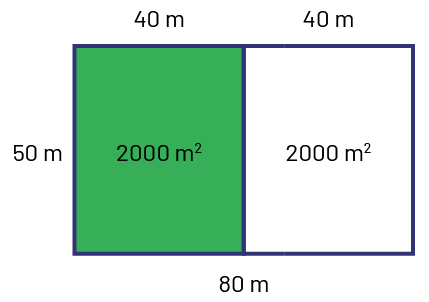 |
50% of the land is covered with grass. | Even if 50% of the field is covered with grass, it does not mean that the field has an area of 100 m2. The entire field is 4000 m2. If half of it is covered with grass, there would be 2000 m2 of grass. Thus, \(\frac{2000}{4000} = \frac{1}{2} = \frac{{50}}{100} = 50\% \). |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 34-35.
