B2.5 Add and subtract fractions with like denominators, in various contexts.
Skill: Adding and Subtracting Fractions With Like Denominators, in Various Contexts
Making Connections Between Operations on Whole Numbers and Operations on Fractions
Students have already developed a solid understanding of addition and subtraction. It is important to make connections between operations on whole numbers and operations on fractions. For example, adding 3 eighths and 2 eighths is the same as adding 3 candies and 2 candies. Only the notation is different.
Valuing Informal Procedures to Develop Strategies
It is important to value informal procedures, as they contribute to the development of number sense and operation sense. In situations that involve operations, many students use personal algorithms rather than procedures. For example, a student with good number sense might approach the addition of \(\frac{7}{8}\) of a sandwich and \(\frac{4}{8}\) of another identical sandwich in this way: "I know that with \(\frac{7}{8}\) of a sandwich, I have \(\frac{1}{8}\) less than a whole sandwich. So if I add \(\frac{1}{8}\) to \(\frac{7}{8}\), I have a whole sandwich and I'm left with \(\frac{3}{8 }\) of the second sandwich. So altogether I have \(\frac{7}{8}\; + \;\frac{4}{{8\;}}\; = \;1\frac{3}{8}\) sandwiches".
Nature of the Fundamental Operations
Applying an operation on numbers has the effect of changing the quantities involved. It is very important that students understand this facet of quantity when using addition, subtraction, multiplication and division.
Junior students have had the opportunity to learn about this relationship with respect to the four operations on whole numbers. For addition, two quantities are put together and result in a new quantity while in subtraction, one quantity is taken away from another quantity to result in a new quantity. We can also recognize when we are looking for the difference between two given quantities. Whether one is joining, comparing, combining, or separating quantities, it is important to know and understand how an operation impacts the quantities.
When fractions are involved, it becomes even more important to focus on the meaning of the operation, choose an appropriate model, and think about the quantities. Building a sense of operations on fractions takes a lot of time, as it requires thinking about the numerators, denominators, and wholes involved. Students should be given the opportunity to work with concrete and visual (semi-concrete) models and to develop a sense of the result of performing an operation before moving on to operations involving symbolic representations.
Addition and Subtraction
In Grade 5, students learn about adding and subtracting fractions with like denominators. This is essentially like the addition and subtraction of objects or quantities of the same type, because the fractions have the same unit fraction. For example, in \(\frac{3}{7}\; + \;\frac{2}{7}\; = \;\frac{5}{7}\), the addition simply represents 3 sevenths + 2 sevenths = 5 sevenths, just like 3 apples + 2 apples = 5 apples. In this example, sevenths are counted the same way as apples. We have 3 pieces of a certain size and 2 pieces of the same size, which gives 5 pieces of this size. Adding fractions becomes more complex when the fractions have different denominators, since the parts are not the same size and are not of the same type. These operations are studied in Grade 6.
Subtraction is treated the same way. For example, if I take 3 marbles out of a bag that contains 5 marbles, I have 2 marbles left. Similarly, if I subtract 3 eighths from 5 eighths, I have 2 eighths left \(\frac{5}{8}\; - \frac{3}{8}\; = \frac{2}{8}\).
Adding two whole numbers has the effect of increasing the original quantity, while subtracting two whole numbers has the effect of decreasing the original quantity. It is important for students to understand that the same is true for adding and subtracting fractions. This allows them to understand the reasonableness of some answers obtained from incorrect procedures. For example, a student who adds the numerators and denominators of \(\frac{2}{3}\; + \;\frac{1}{3}\) to obtain \(\frac{3}{6}\) should see that this answer, which is equal to \(\frac{1}{2}\), is less than one of the original fractions, \(\frac{2}{3}\).
Exploring Operations Using Multiple Models
It is important for students to learn fraction-related concepts in a variety of situations using a variety of models such as area models, linear models, and set models. The same is true for learning operations on fractions.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 75-77.
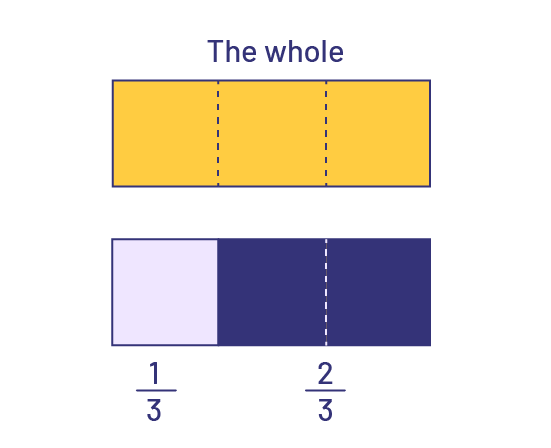
When working with fractions, the most important and sometimes the most difficult thing is to represent the whole correctly. In Grade 5, students add and subtract fractions with like denominators. With concrete or visual (semi-concrete) materials, the visual effect of addition and subtraction is enhanced. Drawing on their experiences with whole numbers and developing operation sense, students may recognize, for example, that adding 2 thirds (\(\frac{2}{3}\)) to 1 third (\(\frac{1}{3}\)) gives 3 thirds (\(\frac{3}{3}\)), or one whole.
However, it is not always clear to students that the actual addition involves the numerator. In a situation where there are 3 eighths left of a pizza and 2 eighths left of another pizza of the same size, we look at how many are left in total. Are we counting eighths or sixteenths, since the pizzas had a total of 16 pieces? Students need to understand that the fraction always relates to the whole, which in this case is 8 pieces. One whole pizza has 8 pieces and each piece of pizza is \(\frac{1}{8}\) of the pizza, so we are adding eighths.
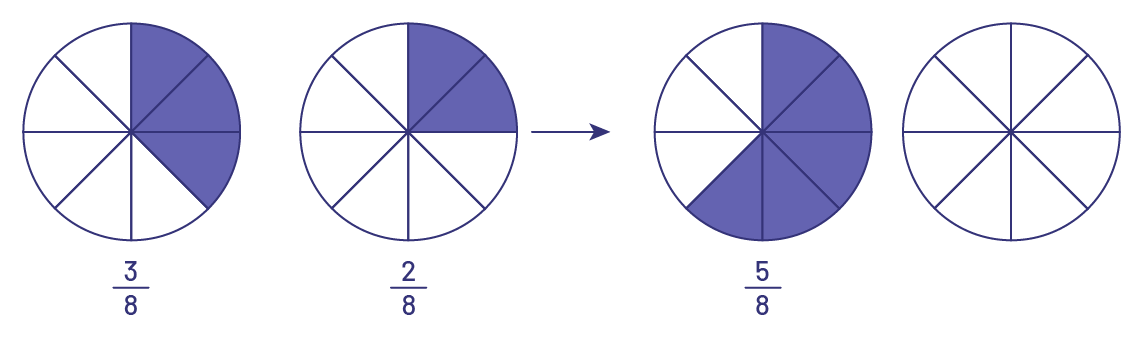
Students should also explore situations involving improper fractions. For example, the operation \(\frac{{10}}{4}\; + \;\frac{3}{4}\) could be represented using the following model.
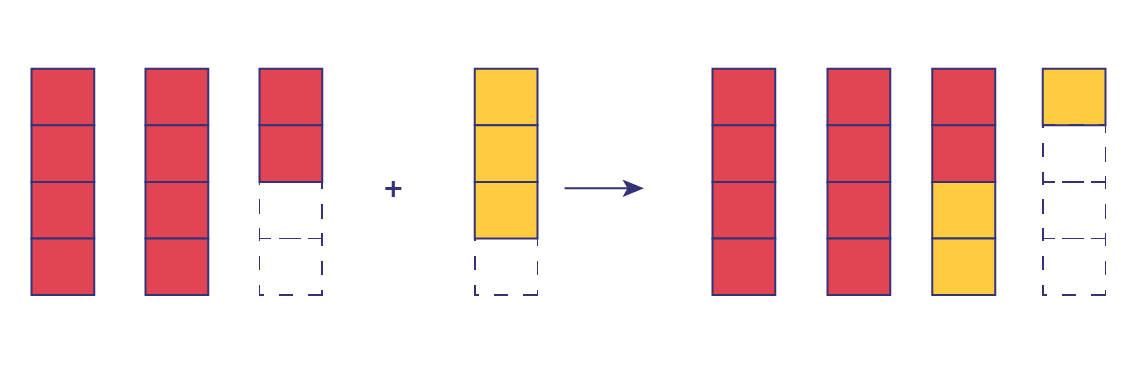
This model allows the result to be expressed in the form \(\frac{{13}}{4}\) or \(3\frac{1}{4}\).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 92-94.
Examples
Joining Problems
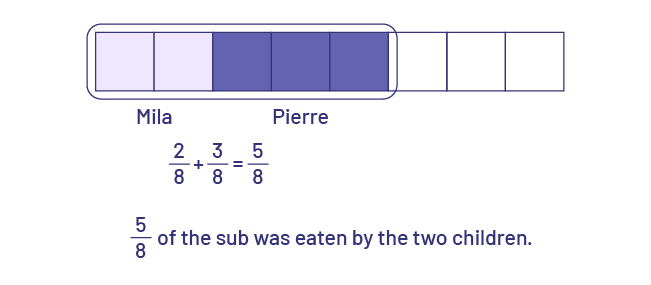
Mila ate \(\frac{2}{8}\) of a submarine sandwich, while Peter ate \(\frac{3}{8}\). What fraction of the submarine sandwich was eaten by the 2 children?
Comparing Problem
Mila used \(\frac{2}{8}\) of a pitcher to water her plant. Pierre used \(\frac{5}{8}\) of the pitcher to water his plant. What is the difference between the amounts of water used by Pierre and Mila?
This situation translates to \(\frac{5}{8}\; - \;\frac{2}{8}\; = \;\frac{3}{8}\).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 78.
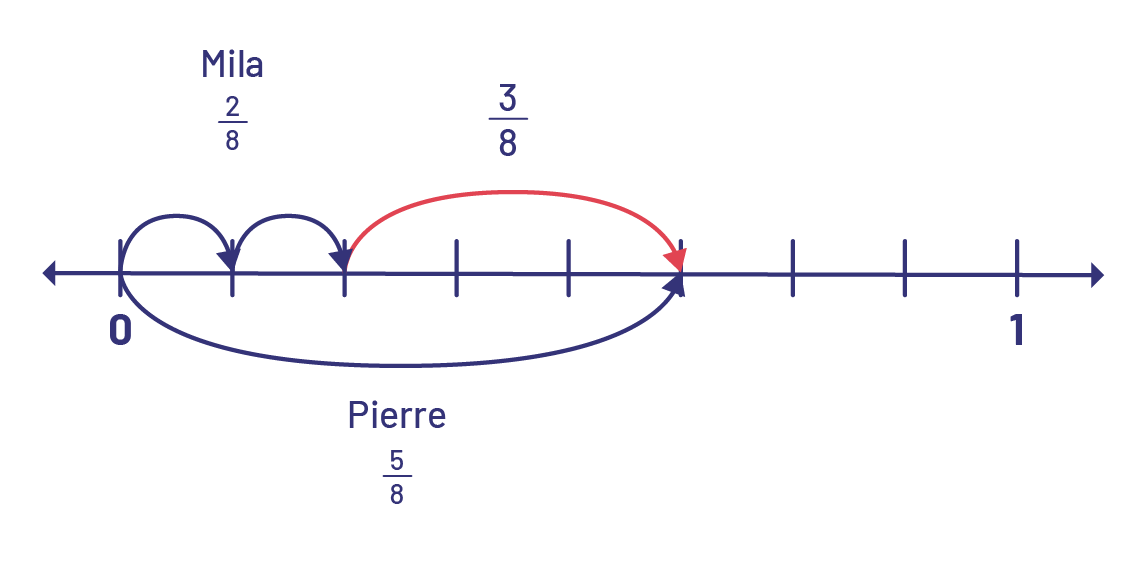
There is a difference of \(\frac{3}{8}\) of a pitcher used by Pierre and Mila.
Knowledge: Numerator
Number of equal parts of the whole being considered.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 34.
The numerator is the number at the top of the fraction. It tells us the number of equal parts or groups involved.
Knowledge: Denominator
Number of equivalent parts by which the whole or set is divided.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 34.
The denominator is the number at the bottom of the fraction. This number allows us to know how many equivalent parts there are in the whole. When there are fractions with like denominators, this means that their denominators are the same and they share the same unit fraction.
