B1.3 Represent equivalent fractions from halves to twelfths, including improper fractions and mixed numbers, using appropriate tools, in various contexts.
Activity 1: Determining Equivalent Fractions Using Various Models
The following are representations that allow the student to develop a sense of what equivalent fractions are.
Linear Model
The linear model is very useful for representing fractions, finding equivalent fractions and performing operations with fractions. It is a very effective visual reference for students to better understand the quantity represented by a fraction.
Interactive activity: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
The same thing can be represented with strips of cm grid paper, with the length of the whole being 36 squares. Various fractions can be constructed with additional strips cut into two for halves, into three for thirds, into four for fourths, and so on. Ask students to make their own fraction set with paper strips.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Area Model
Present the following problem and ask students to solve it using an area model:
- The red part represents the part of the crepe that Mona ate.
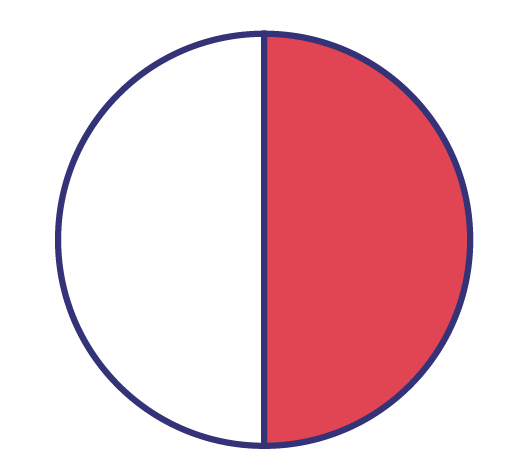
- If this crepe had been cut into 4, 6 or 8 equal parts, would Mona have been able to eat the same amount?
Source: translated from L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Set Model
Present the following problem and ask students to solve it using a set model:
Janika states that three twelfths of the name of the months begin with the letter "J". She uses counters to show her thinking. She uses green counters to represent months that start with a "J" and red counters to represent months that start with any other letter than "J". Will her representation prove her conjecture?
Source: translated from L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Activity 2: Equivalent Fractions
Directions
Hand out the worksheet to the students.
Ask students to write the fraction that represents the shaded area to the right of each rectangle.
Ask students to shade an area on the other rectangles equal to the shaded area on the first rectangle.
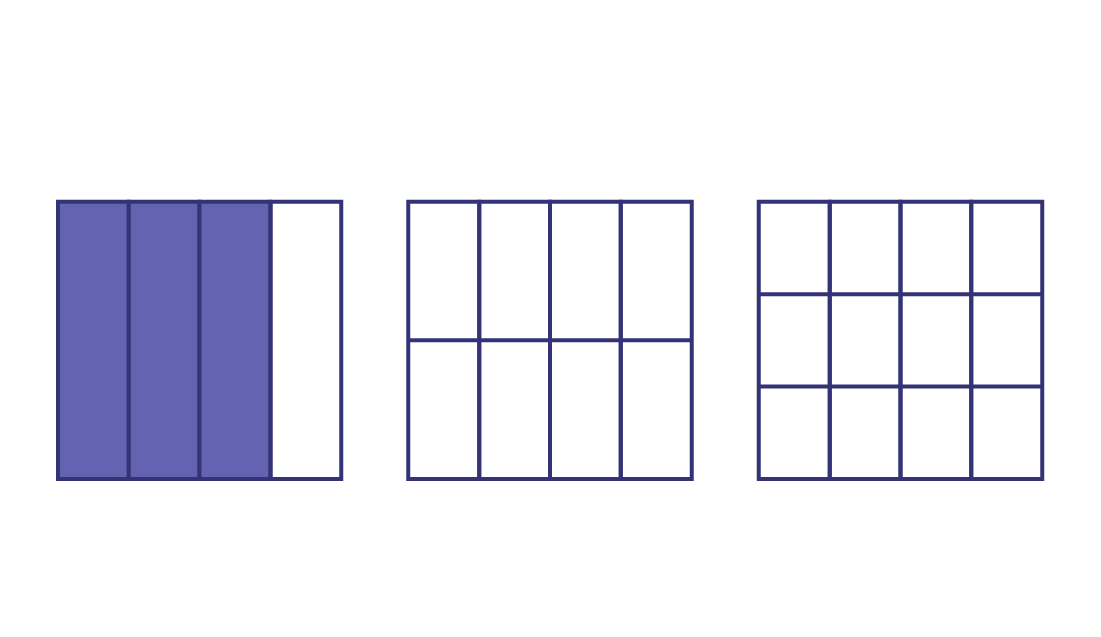
On the board, write the following equalities:

Ask students to explain what they notice about the relationship between the numerators and denominators. Annotate their thinking using arrows and operations on the board diagram.
Ask students to determine a rule for creating sets of equivalent fractions.
Have students use manipulatives to demonstrate the rule they found.
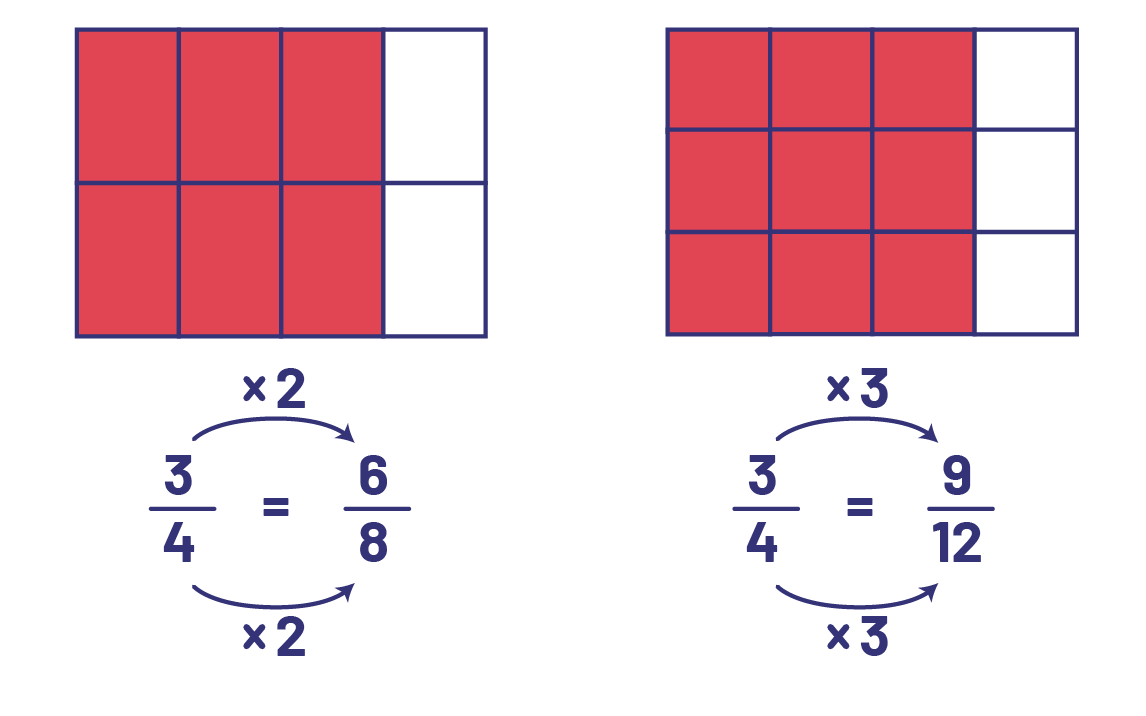
Source: translated from L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Activity 3: Mixed Numbers and Improper Fractions
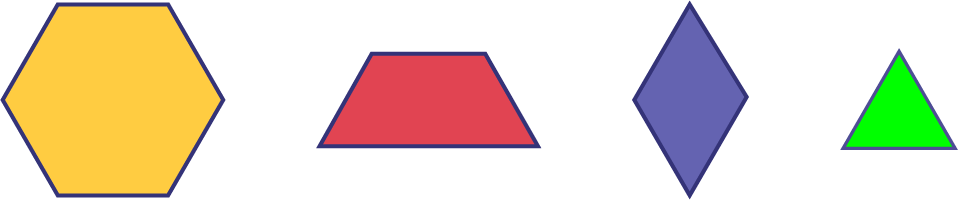
Group the students into two or three and give them pattern blocks. Introduce the blocks by identifying the hexagon as the whole. Have the students recognize that the red trapezoid is equivalent to \(\frac{1}{2}\) of the hexagon, the blue diamond to \(\frac{1}{3}\) of the hexagon and the green triangle to \(\frac{1}{6}\) of the hexagon.
First, ask students to represent \(\frac{{16}}{3}\) hexagons using pattern blocks. Since the improper fraction is in thirds and the diamond represents \(\frac{1}{3}\) of the whole, students should choose 16 diamonds.

Invite students to group the diamonds to form wholes. In this way, students can determine the mixed number that corresponds to the given improper fraction.
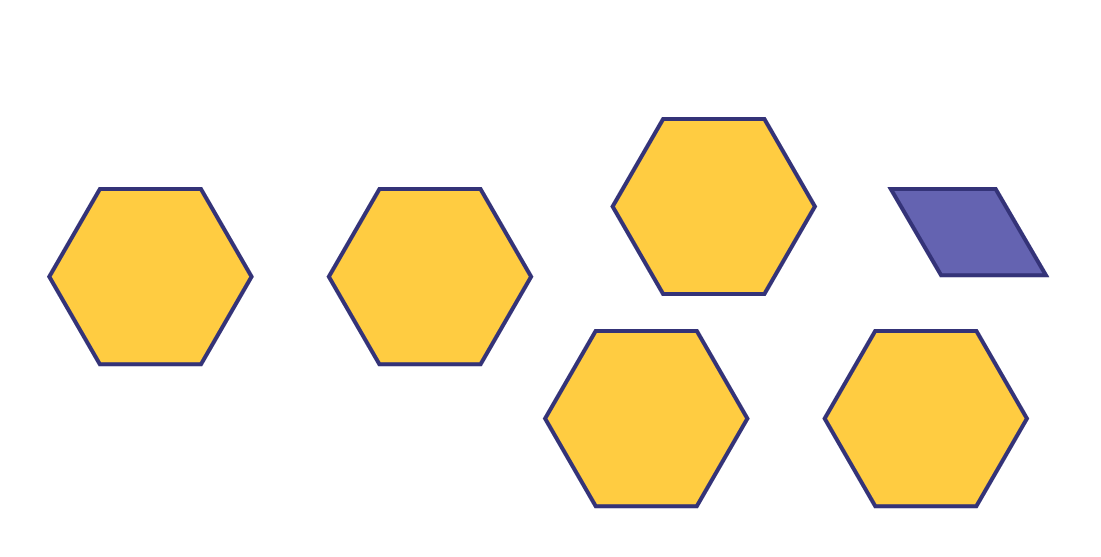
Conclude by pointing out that the given improper fraction (\(\frac{{16}}{3}\)) and the determined mixed number (\(5\frac{1}{3}\)) represent the same quantity.
Following the same approach, explore other equivalences (for example, \(\frac{{13}}{2}\; = \;6\frac{1}{2},\;\frac{27}{6}\;= \;4\frac{3}{6}\)) with the students. After a few examples, ask them to carefully consider the reasoning used to determine a strategy that does not require concrete materials.
Next, ask the students to represent \(3\frac{5}{6}\) hexagons using pattern blocks. To represent the given mixed number, most students will choose 3 hexagons and 5 triangles.
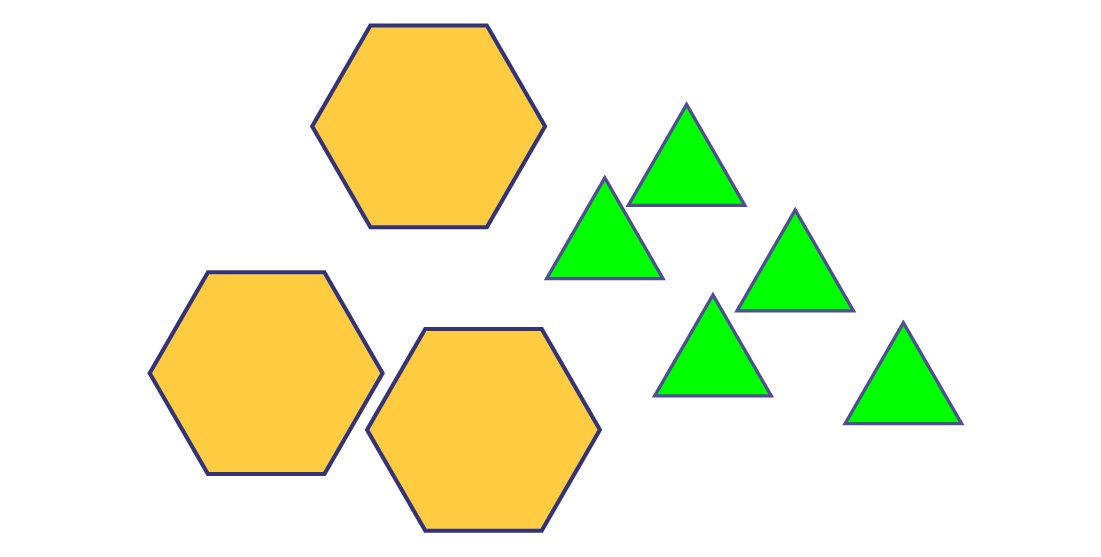
Invite students to use only green triangles to form the wholes. In this way, students can then determine the improper fraction that corresponds to the given number.

Conclude by pointing out that the mixed number \(3\frac{5}{6}\) and the determined improper fraction \(\frac{{23}}{6}\) represent the same quantity. Following the same approach, explore other equivalences (for example, \(7\frac{1}{2}\; = \;\frac{{15}}{2};\;3\frac{2} {3}\;=\;\frac{{11}}{3}\)) with the students. After a few examples, ask them to carefully consider the reasoning used to determine a strategy that does not require concrete materials.
Note: This activity can be done with other types of manipulatives (for example, relational rods, interlocking cubes). In addition, to deepen student understanding of the relationship between a fraction and its whole, the whole can be modified; for example, if the whole is 2 hexagons, then the green triangle is equivalent to \(\frac{1}{{12}}\) of the whole, the blue diamond is equivalent to \(\frac{1}{6}\) of the whole, and the red trapezoid is equivalent to \(\frac{1}{4}\) of the whole.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 157-159.
Activity 4: Flags
Suggest that the students create a class flag that will have four elements of equal importance and will therefore need four equivalent sections.
Provide students with a sheet of paper showing several congruent rectangles. First, ask them to divide the rectangles into fourths in various ways.
Then invite students to draw the rectangle on the board. Discuss the various possible ways it could be divided. Generally, the whole is divided into two equal parts and each of these parts is then divided into two equal parts. Each part is therefore one half of one half, which is one fourth of the whole.
Point out to students that although the shapes of the parts differ, each part covers the same area, one fourth of the rectangle.
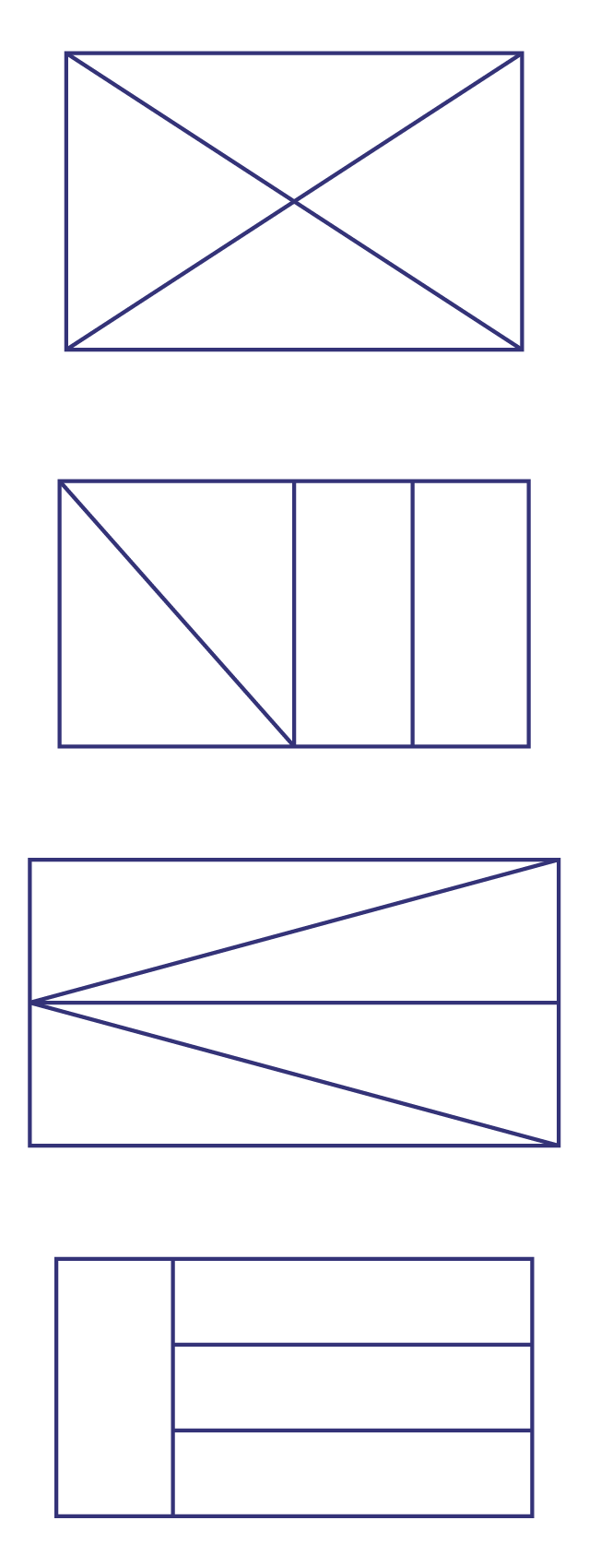
Invite students to choose one of the divided rectangles and create a flag respecting the criterion of the four elements having equal importance.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 135.
