B2.9 Represent and create equivalent ratios and rates, using a variety of tools and models, in various contexts.
Activity 1: Scale Model
This activity integrates concepts from Number, Science and Technology, and The Arts.
The teacher explains that a toy manufacturer has given them a sketch of one of their dollhouses. The teacher shows the students the sketch, focusing on its dimensions and the fact that it is made of rectangle-based prisms.
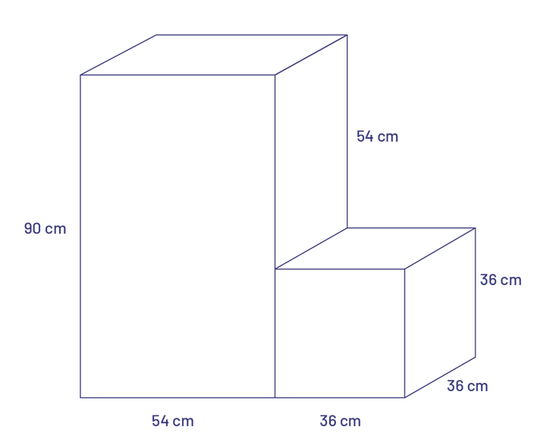
Then, the teacher invites students to create a model of this house with measurements reduced by half (the ratio between the measurements of the model and those of the sketch is 1 to 2). Depending on the skills of the students and the materials available, other ratios can be given to make the model; for example, the measurements are reduced to one fourth (ratio \(1\;:\;4\)), to two thirds (ratio \(2\;:\;3\)) or even doubled (ratio \(2:1\)).
After forming teams of 2, the teacher provides the students with large sheets of cardboard (for example, Bristol board), scissors, rulers, glue, and masking tape or tape, and allow them sufficient time to complete the task (time can also be allowed for decoration, if possible). To complete the task, students can trace the net of the 2 rectangle-based prisms on large sheets of cardboard. They then cut them out and build their model.
Once the task is completed, teachers facilitate a class discussion that highlights the various strategies used to build the models.
Note: This activity could be done using other types of plans such as a bridge, tower, simple machine, or landscaping plan.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 108-109.
Activity 2: Matching Game
Ask students to create cards representing equivalent rates and ratios using images.
Prepare cards with the rate or ratio written symbolically. For example, \(2:1\), \(1: 5\), \(\$5/15\), etc.
Distribute a card to each student and have them circulate to find the card that represents the same rate or ratio.
This game could also be placed in a learning center.
Activity 3: Equivalent Ratios
It is important that students understand what an equivalent ratio is. If students are only learning to do calculations, they will not develop an understanding of this concept.
For example \(4\;:\;5\) is equivalent to the ratio \(8\;:\;10\). Students need to understand not only the multiplicative relationship between the 2 ratios, but understand what they represent. If there are 4 red apples for every 5 green apples, there must be 8 red apples for every 10 green apples.
To check and observe if students understand the concept of equivalent ratio, ask them to represent either with manipulatives or a diagram why \(4\;:\;5\) is not equivalent to \(5\;:\;6\) or why \(4\;:\;5\) is equivalent to \(12\;:\;15\).
Activity 4: Fruit Ratios
Present this fruit situation to the students.
Students can create and represent a ratio from a set of fruits. If there are 15 fruits (10 pears and 5 bananas), they can make ratios such as:
- 10 pears for 5 bananas or \(10\;:\;5\) or \(\frac{10}{5}\)
- 5 bananas for 15 fruits or \(5\;:\;15\) or \(\frac{5}{15}\)
- 10 pears for 15 fruits or \(10\;:\;15\) or \(\frac{10}{15}\)
Students in Grade 5 also learn the concept of equivalent ratios or rates. In the fruit example above, the ratios mentioned above can be represented by equivalent ratios. This concept of equivalent ratios develops proportional reasoning.
- 10 pears for 5 bananas or \(10\;:\;5\) or \(\frac{10}{5}\) or \(\frac{2}{1}\) since we can say that for every set of 2 pears, there is 1 banana.
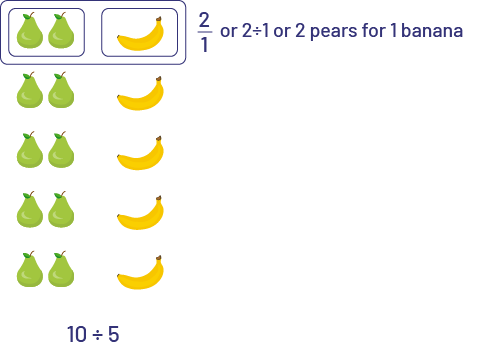
- 5 bananas for 15 fruits or \(5\;:\;15\) or \(\frac{5}{15}\) or \(\frac{1}{3}\) since we can say that there is 1 banana for every set of 3 fruits.
- 10 pears for 15 fruits or \(10\;:\;15\) or \(\frac{10}{15}\) or \(\frac{2}{3}\) since we can say that there are 2 pears for every set of 3 fruits.
We can represent banana : pear ratios using a ratio table.
In this table, we can also recognize that there is a proportional relationship between the number of bananas and the number of pears, that is \(\times 2\). The factor is 2. We multiply the number of bananas by 2 to get the number of pears.
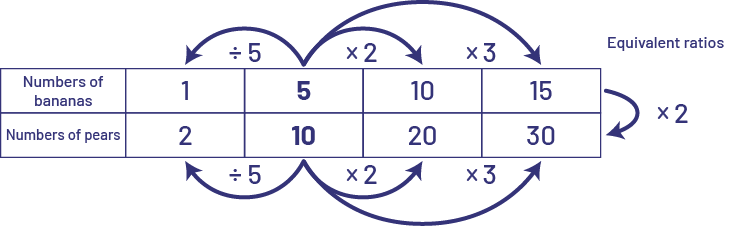
We can therefore say that the equivalent ratios are :
\(\frac{1}{2}\; = \;\frac{5}{10}\; = \;\frac{10}{20}\; = \;\frac{15}{30}\) or \(1\;:\;2\; = \;5\;:\;10\; = \;15\;:\;30\).