B1.1 Represent and compare whole numbers up to and including one billion, including in expanded form using powers of ten, and describe various ways they are used in everyday life.
Skill: Representing Whole Numbers Up to and Including One Billion
The base ten number system commonly used today in many countries uses 10 different symbols, namely the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. It is a positional system since the symbols are given different values depending on their position in a number. For example, the digit 2 has a value of 2 ones in the number 1 356 742, while it has a value of 20 000 ones in the number 5 623 487. Understanding the relationships between the value of digits and their position in a number is essential to the development of number sense.
In the Primary Division, students develop an understanding of the relationships between the place values of ones, tens and hundreds. However, once in the Junior and Intermediate Divisions, they do not automatically transfer this understanding to larger numbers. This is why teachers must ensure that students understand that the value of any position in a number is always 10 times greater than the value of the position immediately to the right, and 10 times less than the value of the position immediately to the left. It is also important to examine the relationships of 100 times or 1000 times greater or lesser between place values in order to support students in developing a deep number sense, especially with respect to large numbers.

Students should also recognize, for example, that 10 000 represents a grouping of 10 one thousands, 100 hundreds, 1000 tens, or even 10 000 ones. These regroupings allow students to recognize equivalent representations of numbers (for example, 2534 represents 25 hundreds and 34 ones).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 44-45.
Students should learn to represent numbers in a variety of ways and recognize them in multiple representations. These skills will help them make connections between a number, its representation, and the quantity it represents. Therefore, it is essential to expose students to different representations of numbers. It is also important to introduce them to a variety of contexts that will lead them to represent a number in the different ways shown in the following diagram. In time, students should ideally move flexibly from one representation to another.
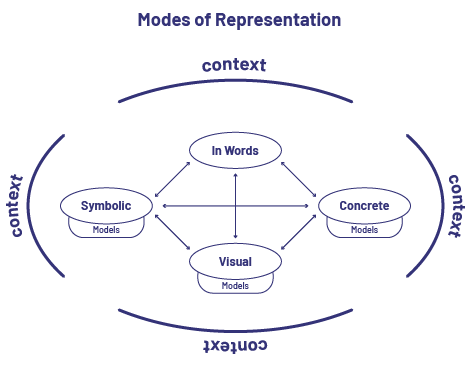
Teachers need to be aware of the order in which they should introduce into these four modes of representation with students. Baroody and Coslick (1998) suggest that a new concept should be presented in a real and meaningful context so that students can first create representations using words, then concrete and visual (semi-concrete) representations. Only when they have developed some understanding of the concept can they move on to its symbolic representation. Students should be able to make connections between representations and move easily from one representation to another.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 64-65.
Representations Using Words
Number is an abstract representation of a very complex concept. For this reason, the relationship between the way a number is named and the quantity it represents is not obvious to students. Many adults mistakenly believe that if students can count, they understand the meaning of each number. However, a student may be able to read and name a number, such as 3 000 047, without really having a sense of the quantity it represents.
In the Junior Division, students learn to read and write numbers up to one million and in the Intermediate Division, up to one billion. The challenges of writing numbers in words should not be underestimated. To help students overcome these challenges, teachers should include numbers on the word wall and build reference materials with them.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 65-66.
Symbolic Representations
Numbers are represented symbolically by the digits that make them up. They are written from left to right in 3-digit periods that make up the trillions, billions, millions, thousands and ones. Each of the periods includes hundreds (h), tens (t) and ones (o).

Notes:
- In French, the term "billion" does not have the same meaning as the English term billion. A French billion corresponds to an English trillion.
- In English as well as in French, numbers are written by adding a space between the 3-digit periods (for example, 13 567 232). Writing 4-digit numbers without using a space is accepted (for example, 3543).
The writing of large numbers requires a good mastery of the concept of place value, otherwise the student who is asked to write symbolically "one thousand two hundred thirteen" could write 1000 200 13 or 1000 213 or 1200 13. It also requires an understanding of the role of the 0 to indicate the absence of a quantity in one of the positions.
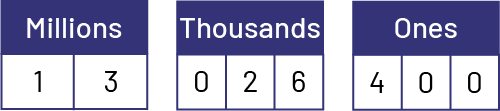
Example of reasoning that students might use to symbolically represent a large number such as "thirteen million twenty-six thousand four hundred" include:
- thirteen million is represented by 1 and 3 in the millions period, which implies that there are 6 positions to the right of it to fill;
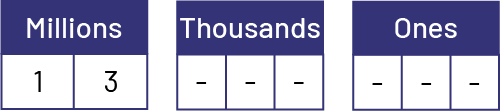
- twenty-six thousand is represented by 2 and 6 in the thousands period, but it is necessary to insert a 0 in the position of hundreds of thousand, because the word "hundred" is not heard in this period;

- four hundred is represented by a 4 in the hundreds position of the ones period. Since there is no indication for the tens and ones position, a 0 must be added to fill each of these positions.

- thirteen million twenty-six thousand four hundred written symbolically gives 13 026 400.
A number can be represented in different ways using mathematical symbols, either by respecting the value of the position of each digit \(1236\) is equal to \(1000\; + \;200\; + \;30\; + \;6\), or from some place values (1236 equals 12 hundreds and 36 ones) or by performing different operations \(1236\) equals \(1000\; + \;236\) or \(1240\; - \;4\) or \(1200\; + \;36\) or \(1000\; + \;100\; + \;100\; + \;15\; + \;15\; + \;6\). In fact, there are an infinite number of ways to represent a number, each of which allows students to develop a different way of interpreting it and understanding its meaning.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 70-71.
Equality Relationships
A number is represented symbolically using digits. For example, the number one thousand two hundred fifty-six written symbolically gives 1256. It can also be represented using various numerical expressions. For example, the representation \(1000\; + \;200\; + \;50\; + \;6\) allows you to recognize 1256 according to the place value of the digits that make it up. There are many other ways to decompose or represent this number.

Equality relationships make it possible to establish equivalence between various representations of the same quantity. Exploring multiple representations of a number helps students develop a better understanding of the meaning of that number. In problem-solving situations, students must learn to choose the representation that is the most appropriate for the context and intention.
Examples include:
To Compare Numbers
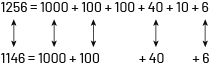
\(\ 25\; \times \;9\; = \;25\; \times \;(10\; - \;1)\)
\(\ 25\; \times \;9\; = \;(25\; \times \;10)\; - \;(25\; \times \;1)\)
\(\ 25\; \times \;9\; = \;(250\; - \;25)\)
Then \(\ 25 \times \;9\; = \;225\)
To Do Mental Math
\(\begin{array}{l}325\; + \;527\; = \;325\; + \;525\; + \;2\\325\; + \;527\; = \;850 \; + \;2\\325\; + \;527\; = \;852\end{array}\)
To Estimate
\(\ 24\; \times \;26\) is close to \(\ 25\; \times \;25\)
\(\ 25\; \times \;25\; = \;25\; \times \;(20\; + \;5)\)
\(\ 25\; \times \;25\; = \;(25\; \times \;20)\; + \;(25\; \times \;5)\)
\(25\; \times \;25\; = \;500\; + \;125\)
\(25\; \times \;25\; = \;625\)
Thus, we can say that \(24 \times 26 \) is about 625.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 48-49.
Large numbers can be expressed as decimal numbers by expressing the place value in words. For example, 36.2 million is 36 200 000 = (36.2; times; 10^6).
Expanded notation with powers of ten shows a number as an expression by using addition, multiplication, and exponents. The number “three hundred seven million, twenty thousand, and fifty”, can be expressed as 307 020 050 and \(3\; \times \;{10^8}\; + \;7\; \times \;{10^6} \; + \;2\; \times \;{10^4} + \;5\; \times \;10\).
Source: Ontario Curriculum. Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Skill: Comparing Whole Numbers Up To and Including One Billion
Numbers can be compared by their place value or they can be compared using proportional reasoning. For example, 1 billion is 1000 times greater than 1 million.
Source: Ontario Curriculum. Mathematics Curriculum, Grades 1-8 2020, Ontario Ministry of Education.
Order Relationships
The ability to recognize order relationships is acquired by comparing numbers, decomposing them, placing them in ascending and descending order, counting backwards and analyzing the relative proximity of two numbers.
In the Intermediate Division, students are expected to recognize the order relationship between numbers by comparing them. They can describe the relationship by stating, for example, that 350 198 052 is less than 432 840 590. The following are examples of strategies they can use to compare large numbers.
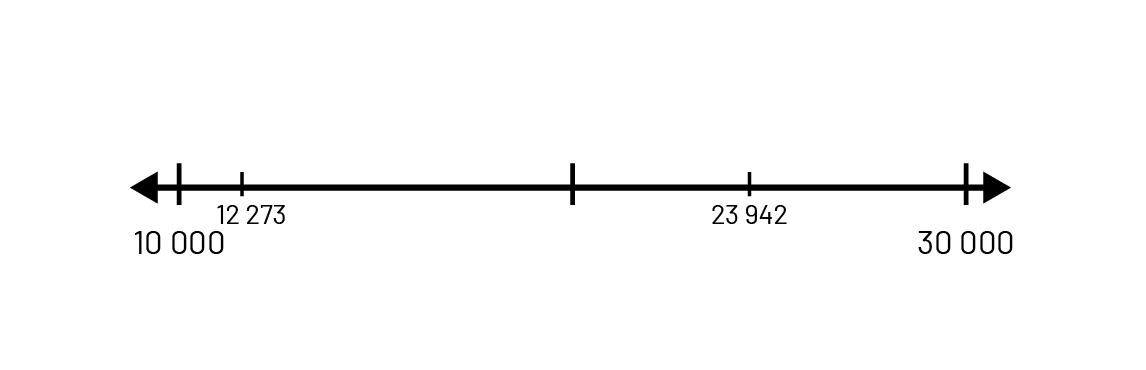
Comparison of the numbers 23 942 and 12 273
Students can recognize that 23 942 is larger than 12 273:
- by targeting a significant portion of each number (note that 23 000 is greater than 12 000);
- by visualizing large quantities (visualize 23 groupings of 1000 and 12 groupings of 1000);

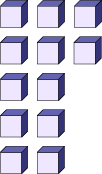
- by locating the numbers on a number line (the number 23 942 is located to the right of the number 12 273 indicating it is greater);
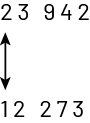
- by comparing the numbers in the various positions from the left (2 represents 20 000 while 1 represents 10 000);
- by comparing the position values expressed using the power of 10.
| Shanghai | \[2\; \times \;{10^7}\; + \;7\; \times \;{10^6}\; + \;7\; \times \;{10^5} + \;9\; \times \;{10^4}\; + \;6\; \times \;{10^3}\] |
| Tokyo | \[3\; \times \;{10^7}\; + \;7\; \times \;{10^6}\; + \;3\; \times \;{10^5} + \;4\; \times \;{10^4}\] |
| Sao Paulo | \[2\; \times \;{10^7}\; + \;2\; \times \;{10^6}\; + \;2\; \times \;{10^5} + \;3\; \times \;{10^4}\; + \;7\; \times \;{10^3}\] |
| Delhi | \[3\; \times \;{10^7}\; + \;1\; \times \;{10^6}\; + \;1\; \times \;{10^5} + \;8\; \times \;{10^4}\; + \;1\; \times \;{10^3}\] |
Tokyo and Delhi have a higher value at the tens of millions position (107) (3 tens of millions compared to 2 tens of millions)
Source: translated from En avant, les maths! 7e, CM, Nombres, p. 5.
To help students develop the skill of recognizing order relationships among large numbers, teachers can, starting with a given number, ask them to count up by 1 (for example, 12 998, 12 999, 13 000, 13 001…) or by intervals (for example, 32 200, 32 400, 32 600…) and count backwards by 1 (for example, 26 271, 26 270, 26 269…) or by intervals (for example, 45 650, 45 600, 45 550…).
These activities help students recognize that when counting by 1s or intervals, any named number is greater than those before it and less than those after it, whereas when counting backwards by 1s or intervals, any named number is less than those before it and greater than those after it. While these relationships may seem obvious to adults, students often get them wrong because they do not consider the concept of grouping. When asked, for example, what number comes before 300, many students tend to spontaneously answer 399 because their attention is focused on the two 0s; they know that a number ending in two 0s is always preceded by a number ending in two 9s, and they forget to consider the regrouping by hundreds that occurs. In contrast, when the same problem is posed in context, students give more thoughtful responses; for example, in a situation where a person has 300 field hockey cards and loses one, students will readily respond that they have 299 cards left.
Once students have mastered the relationships "greater than" and "less than," they need to learn to make these relationships more specific by drawing on their understanding of quantity. They then use expressions such as close to, about, the same as, much more than , and a little less than. For example, students may say that the population of a village of 15 239 is about 15 000; that 304 is a little more than 300; that 12 894 is a little less than 13 000; that 32 523 is about a hundred more than 32 432; and that 620 and 618 are closer together than 630 and 680.
This ability to specify order relationships between numbers becomes important when students use numbers in problem solving, rounding, estimating and comparing. The following activity allows students to demonstrate this skill.
Draw a number line on the board to represent any interval (for example., 1000 to 2000). Place some letters (for example, A, B, C, D) in this interval as shown below.

Ask a few students to come and locate some numbers on the line (for example, 1873, 1332, 1167). Then ask them to describe the ordering relationships that exist between the numbers and the letters.
For example, students might say:
- that 1167 is between A and B;
- that the letters B and C are between 1167 and 1332;
- that the number 1873 is closer to 2000 than to the letter D;
- that the letter B seems to be more in the center of the interval between 1000 and 1500 than the letter C.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 45-48.
Skill: Describing the Ways in Which Numbers are Used in Everyday Life
Context is all the information surrounding a given situation. This information helps to identify the situation in which the quantities are used and facilitates the exercise of a critical eye on the numbers in question. In addition, the context facilitates the establishment of connections between numbers, mathematical concepts and the mathematical world. For all these reasons, the exploration of mathematics in problem-solving situations is powerful.
What does 21 560 814 mean exactly? We are talking about 21 560 814 "what"? In short, a number without context has little meaning. Therefore, it must be accompanied by units if it is to be understood. Students in the Primary Division have already engaged in number activities in a variety of contexts using a variety of units. In the Junior and Intermediate Divisions, this contextualization must be maintained in order to develop a sense of quantity, and this must be done with numbers in the thousands and millions.
An important step is to support students in understanding that the same number represents the same quantity even though the contexts are different. The number is the symbolic representation of the quantity. If one has 100 000 apples, 100 000 heartbeats, or 100 000 buildings, the quantity that is 100 000 does not change. Yet, if students are asked if they believe there are more apples than buildings, many are likely to respond that there are more buildings than apples. They focus on the space occupied by the objects rather than the quantity of objects (100 000).
Students should also recognize that depending on the context of the given situation, different interpretations can be made of the same quantity. For example, for young people, $100 may represent a lot of money. However, in context, the meaning of the number invites nuance: it is a lot for the price of a sweater, but not much for the price of a new bicycle. The context changes, but the quantity remains the same. Similarly, 200 000 blocks of wood is a lot of blocks, while 200 000 hairs on the head is the equivalent of an average head of hair. Or, students may consider that 13 is not a large quantity, but if we add that it is the number of our brothers and sisters, it takes on a whole new value. These simple, concrete examples encourage students to think about and critically analyze quantities.
In the Junior and Intermediate Divisions, understanding numbers in context becomes increasingly important. Students need to begin to make critical judgments about quantities and to be discerning about numbers. Learning activities should therefore help students develop other skills, such as recognizing the reasonableness of a given number in a certain context, recognizing that it is an exact value, or recognizing that it is an approximate number resulting from estimation or even rounding. The development of these skills can be initiated by having class discussions about the meaning of numbers from newspapers and discussing their actual meaning and relevance.
The context also allows us to recognize that the same number does not always have the same meaning. The most common interpretation associates them with quantity or cardinal numbers. However, if we look at context, we notice that some numbers do not represent quantities at all, but rather a position, as in the case of ordinal numbers. For example, in a marathon, the runner who is at position 11 582 does not represent 11 582 runners, but rather the 11 582nd person to cross the finish line. The number indicates the position of a single person in the given series. Numbers are also used to label or identify, as the case with social insurance numbers, bar codes, license plates and addresses.

Benchmarks
In general, a benchmark is a mark, a milestone, or a reference. As part of the development of a sense of number, the use of benchmarks promotes mental representation and thus facilitates the understanding of number and the notion of "how much". The benchmarks, without which it is difficult to understand quantity, are numbers or quantities that can be easily represented mentally since they have already been seen and manipulated. Students will have difficulty understanding quantity if they do not use benchmarks.
Benchmark numbers are particularly useful for understanding large numbers, since it is usually impossible to recognize these quantities globally or to grasp them by counting. Students need to get a sense of them by comparing them with a benchmark number. For example, the school just received 10 000 sheets for photocopying. Should the custodian ask for help carrying them? In order for students to truly understand the situation and the quantity involved, they need to create a mental image of what 10 000 sheets might represent. Using a package of 500 sheets as a guide, students can imagine this quantity and apply the proportionality relationship to deduce that two packages contain 1000 sheets. Therefore, 10 000 sheets would be 10 times as many packages, or 20 packages of sheets. We can even recognize that 20 packages are equivalent to two boxes of paper. The mental representation of the space occupied by these 10 000 sheets then becomes possible. The answer to the original question, whether the custodian should ask for help in carrying the sheets, can then be debated with full knowledge.
Students should develop their own personalized benchmarks, depending on the context and the numbers being dealt with. There is no list of benchmarks. They are personal and come from experiences, making them meaningful and easier to use. However, real-life situations provide teachers with ample opportunities to draw their students' attention to the quantity and creation of benchmarks.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 31-35.
Knowledge: Expanded Form
The expanded form is a way of writing numbers that is based on place value and shows the value of each digit.
Example
The number three hundred seven million twenty thousand fifty can be expressed as 307 020 050 or \(3\; \times {10^8}\; + \;7\; \times {10^6}\; + \;2\; \times {10^4}\; + \;5\; \times {10^1}\).
Knowledge: Power of Ten
A power of th number 10 where the number 10 multiplied by itself the number of times indicated by the exponent.
Example
\({10^2} = \;(10 \times 10 \;) = 100\)
Source: translated from En avant, les maths! 7e, CM, Nombres, p. 3.
