B1.3 Read, represent, compare, and order rational numbers, including positive and negative fractions and decimal numbers to thousandths, in various contexts.
Skills: Reading, Representing, Comparing and Ordering Integers
The positive or negative sign indicates whether the number is greater or less than 0. Thus, if the number is positive, it will be placed to the right of 0 on a horizontal number line or over 0 on a vertical number line. If the number is negative, it will be placed to the left of 0 on a horizontal number line or below 0 on a vertical number line. The reference number for integers is therefore always 0.
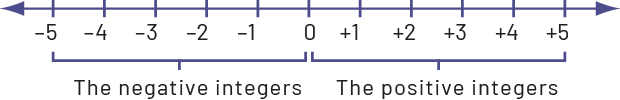
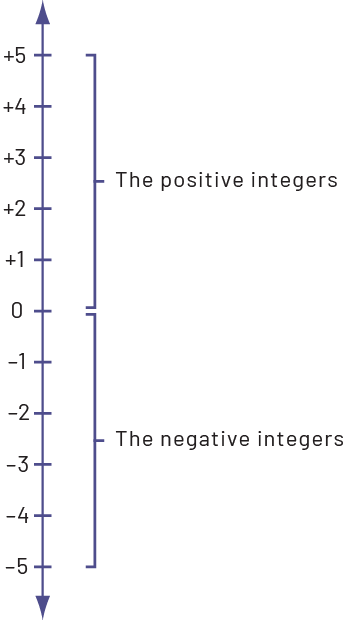
A positive number is always greater than a negative number.
For example, 8 > 2 and -2 > -6.
Using the number line, it is easier to compare and order integers since a number with multiple digits does not necessarily mean it is larger (for example -584 is smaller than 8). By analyzing the line above, we can place the numbers in ascending order (-6, -2, 2, and 8) or descending order (8, 2, -2, and -6).
On the number line, the absolute value of a number is its distance from 0. For example, the absolute value of -3 and 3 is 3 since 3 units separate the 2 numbers from 0.
Source : 1Réduction des écarts de rendement2, 93e 4année, p. 11.
Skill: Reading, Representing, Comparing and Ordering Decimal Numbers
The order relationship is based on the comparison of numbers. One of the great strengths of decimal notation is the speed with which it is possible, through the concept of place values, to compare and order quantities. For example, it is much easier to compare the numbers\(\frac{1}{8}\) and \(\frac{3}{{40}}\) when they are expressed in decimal notation, that is, \(0.125\) and \(0.075\).
In general, students have little difficulty comparing decimal numbers with the same number of decimal places (for example, 0.34; < 0.46). They have more difficulty comparing numbers with different numbers of decimal places (for example, 1.34 and 1.275). Some tend to compare these numbers without the decimal point (for example, 134; < 1 275) and conclude incorrectly that 1.34; < 1.275). Others reach the same incorrect conclusion by comparing only the numbers to the right of the decimal point (for example, \(34\; < \;275\)).
The order relationship should be addressed by comparing decimal numbers in contextualized situations. For example: "Remi did a jump of 3.55 m and Samantha did one of 3.7 m. Which of the two had the longer jump?" Students can respond and justify their choice if they understand place value. The number line is a powerful visual model for comparing decimal numbers. To place 3.7 on a number line, students can represent tenths from 3.0 to 4.0. To place 3.55, they must divide the interval between 3.5 and 3.6 into 10 equal parts, with each space representing one hundredth. They can then conclude that (3.55; < 3.7), so Samantha has taken a longer jump than Remi.
Students who have developed good number sense can also compare 3.55 m and 3.7 m by first noticing that they represent 2 jumps greater than 3 m. Then they can compare tenths to notice that the1st number has 5 tenths, or 5 decimetres, while the2nd has 7.
The2nd jump is therefore longer than the1st. Students can also, after comparing ones, think of 3.7 as 3.70, or 3 metres and 70 centimetres. The number 3.55 represents 3 metres and 55 centimetres. The 3.7-metre jump is therefore longer than the 3.55-metre jump.
Traditionally, a procedure was taught where you had to add a 0 to the end of 3.7 to give 2 numbers with the same number of decimal places. The decimal parts, 55 and 70, were then compared to conclude that 3.70 was greater than 3.55. Although the teaching of the method was accompanied by an explanation, so much emphasis was placed on the procedure that the explanation and the concept were quickly lost. Not surprisingly, young people often answered such questions incorrectly. For example, in an international test ofsixth graders, 87% reported that 6 987 is greater than 6 879, while only 52% concluded that 1.05 is greater than 1.015 (Brissiaud, 1998). Students who understand the concept of place value do not need to apply a procedure to compare decimal numbers.
Open problems, which offer more than one answer and are thought-provoking, allow students to deepen their understanding of order relationships.
- Determine three decimal numbers between \(\frac{3}{40}\) and \(\frac{1}{8}\).
- Determine 3 decimal numbers between 0.555 and 0.623.
- Determine three numbers within one thousandth of 2.869.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 54-55.
Skills: Reading, Representing, Comparing and Ordering Fractions
Order Relationships
It is important that students learn to order fractions by comparing them. The ability to order and the ability to compare should be based on students' constructed representations of fractions. They should arise from problem-solving situations that allow students to develop a sense of the value of a fraction. It is this sense of the fraction that allows students to compare 2 fractions and conclude that one is greater than the other. In contrast, teaching that is done out of context tends to promote learning algorithms that neglect the meaning of the fraction.
Students already have well-established ideas about the properties of whole numbers. However, when they begin to work with fractions, students often face a cognitive imbalance, that is to say a feeling that what was true is no longer true. For example, they learned that in the presence of 2 whole numbers, the greater number indicates a greater quantity. They try to transfer their knowledge and skills to fractions. Thus, when wanting to compare \(\frac{1}{6}\) and \(\frac{1}{3}\), some students believe that \(\frac{1}{6}\) is greater than \(\frac{1}{3}\), since 6 is greater than 3. They feel out of balance if they are told they are wrong. To avoid such situations, learning must be based on an analytical view of the fraction rather than on automatism or an algorithm.
With the introduction of negative fractions, the comparison can also create an imbalance. For example, when wanting to compare \(\frac{1}{6}\) and \( -\frac{1}{3}\), the student could say that \(\frac{1}{6} \) is smaller since sixths are smaller than thirds. However, understanding integers will recognize that any negative number is smaller than a positive number. Here, \( -\frac{1}{3}\) is then smaller than \(\frac{1}{6}\).
Activities that involve students in comparing and ordering fractions should promote the construction of fraction meaning. To compare fractions, it is rarely necessary to look for a common denominator. Thus, there are many strategies for comparing fractions. Generally, the first strategy learned is the use of a concrete or semi-concrete representation of the fractions involved. This strategy can be used on any occasion. One can also compare numerators if the denominators are the same, or compare denominators if the numerators are the same. Another effective strategy is the use of benchmark fractions.
It is important to work thoroughly on the comparison of fractions before the equivalence of fractions. This is very complex and the comparison serves as a catalyst for understanding equivalent fractions.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 44-45.
Skill: Comparing Numbers Expressed in Different Forms
Intermediate students need to understand the relationships between various notations of a quantity, for example, the connections between equivalent decimals and equivalent fractions. They must recognize that a decimal number is a fraction or mixed number whose denominator is a multiple of 10 (10, 100, 1000, 10000, etc.). For example, the number 0.5 (known as "5 tenths") is equivalent to the fraction \(\frac{5}{{10}}\) and the number 2.63 (known as "2 and 63 hundredths") is equivalent to the fractional number \(2\frac{{63}}{{100}}\). Models such as \(10\; \times \;10\) grids allow students to visualize the connections between the corresponding fraction and the corresponding decimal.
Example
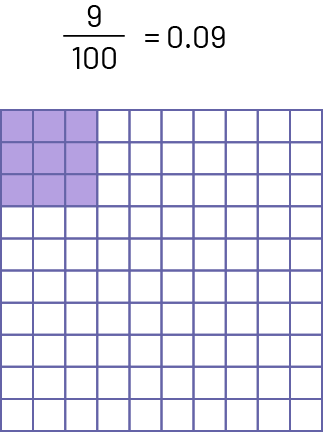
When students have a good grasp of this relationship, they are able to identify equivalent fractions and decimals and choose the form that best suits the context. For example, a merchant must order the exact amount of flour to meet the demand of his customers. The1st customer requires 12.5 kg of flour, the 2nd \(11\frac{3}{4}\) kg, the 3rd \(\frac{{15}}{{10}}\) kg and the 4th \(5\frac{3}{6}\) kg. A student who has mastered the relationship may decide to convert fractions to decimals to simplify the calculation. So, \(11\frac{3}{4}\) kg is equivalent to 11.75 kg, \(\frac{{15}}{{10}}\) kg is equivalent to 1,5 kg and \(5\frac{3}{6}\) kg is the equivalent of 5.5 kg. Again, it is important to emphasize using models to clearly see the relationships between fractions and decimals rather than formally learning a procedure to perform the conversion from one form to another.
Instructional interventions should focus on developing students' versatility with numbers. To do this, teachers should present learning situations that involve a variety of numbers and should emphasize the different ways of writing these numbers, while reflecting on the advantages of one notation over another. This allows students to develop their number sense and expertise in using numbers. It is desirable that students have the opportunity to relate numbers in a variety of forms, including mixed numbers, decimal numbers, positive and negative fractions, etc.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 55-56.
Models, especially if they are proportional like the number line, can be used to order numbers, to reveal the order of magnitude and to show equivalence between rational numbers.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Knowledge: Set of Rational Numbers (ℚ)
The set of rational numbers includes all numbers that can be expressed in fractional form. It includes whole numbers, integers, and decimal numbers, as well as numbers whose decimal expression is infinite and periodic (for example, \(\frac{1}{3}\; = \;0,333\;33...\; = \;0,\mathop {\overline 3 }\limits^{} \) ; \(\frac{5}{{11}}\; = \;0,454\;545...\; = \;0,\mathop {\overline {45} }\limits^{} \); \( - \frac{{421}}{{198}}\; = \;2,126\;126\;6...\; = \;2,\mathop {\overline {126} }\limits^{} \). We can represent the relationship between the sets of numbers by the Venn diagram below.
Set of Decimal Numbers (ⅅ)
Set of Integers (ℤ)
Set of Whole Numbers (ℕ)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 41-43.