B1.4 Use equivalent fractions to simplify fractions, when appropriate, in various contexts.
Skill: Using Equivalent Fractions to Simplify Fractions
Determining equivalent fractions means determining fractions that represent the same quantity. We are looking for a number of "small parts" of a whole that correspond to a particular number of "large parts" of the same whole. For example, if we are looking for the number of sixteenths that corresponds to one fourth (\(\frac{1}{4}\) = \(\frac{?}{{16}}\))
\(\frac{4}{{16}}\) of the same chocolate bar
\(\frac{1}{4}\) of a chocolate bar
Sixteenths are four times smaller than fourths. In a whole, there are 4 times more sixteenths than fourths. In order to represent the same quantity, you need 4 times as many parts \(\left( {4\; \times \;1\; = \;4} \right)\). Four sixteenths are then equivalent to one fourth. This explains the algorithm below.
We can see that the reverse is also true. Since fourths are 4 times larger than sixteenths, four times fewer are needed \(\left( {16\; \div \;4\; = \;4} \right)\). In order to represent the same quantity, there must be four times fewer parts identified (\(4 \div 4 = 1 \)). So, 1 fourth is equivalent to 4 sixteenths. This explains the algorithm on the right.
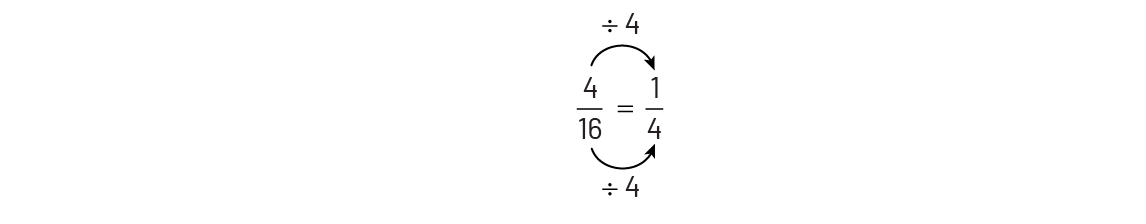
It is essential that students understand and can explain this relationship in order to make sense of the algorithm used to determine equivalent fractions.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 51.
Note: A fraction is simplified (in lowest terms) when the numerator (count) and the denominator (unit) have no common whole number factor other than 1.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8 , 2020, Ontario Ministry of Education.
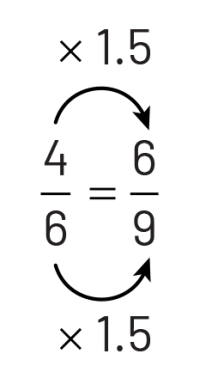
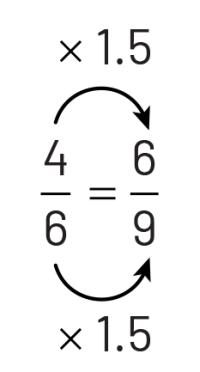
However, it is not always so easy to recognize equivalent fractions. Take, for example, \(\frac{4}{6}\) and \(\frac{6}{9}\). We do not see equivalence as the result of multiplying the numerator and the denominator by an integer, which is the usual algorithm. We can reduce each fraction to its lowest terms to see that each is equivalent to \(\frac{2}{3}\). We can also use a semi-concrete representation:
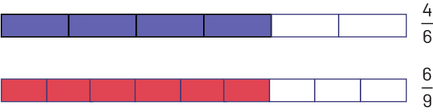
This representation allows us to see the multiplicative aspect. We can see that the sixths are one and a half times bigger than the ninths. To go from the sixths to the ninths, we need 1.5 (\(1\frac{1}{2}\)) times more pieces.
The equivalence relationship should also be explored in relation to fractions of a set (the whole). In the picture below, students can easily see that candy is wrapped in purple wrappers. However, they have difficulty determining other equivalent fractions \(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{6}{9}\)). It is then important to present activities that allow them to manipulate the elements of the set. For example, students can group them into sets of 6, 3, or 2 and determine equivalent fractions.
\(\frac{2}{3}\) candies are wrapped in purple wrappers.
\(\frac{4}{6}\) candies are wrapped in purple wrappers.
\(\frac{6}{9}\) candies are wrapped in purple wrappers.
Concrete experiments with equivalent fractions is the foundation of proportional reasoning. It cannot be overemphasized. Therefore, teachers should plan activities that build on the informal concepts related to equivalent fractions.
A few points need to be made about learning equivalent fractions. First, the focus should not be on the concept of fractions in their lowest terms. It is better to treat these fractions like any other and to focus on equivalent fractions, that is, fractions that are different representations of the same quantity. Second, pay attention to the vocabulary that is used and the students' understanding of it, as well as the vocabulary that students use and understand. For example, some students claim that \(\frac{3}{4}\) and \(\frac{9}{{12}}\) are equivalent fractions, but that \(\frac{3}{4}\) is larger or smaller than \(\frac{9}{{12}}\) or even that it is a "better" fraction. Similarly, some students think that the fraction is smaller than the fraction \(\frac{4}{6}\), since \(\frac{2}{3}\) was obtained when \(\frac{4}{6}\) was simplified. It is important to determine the source of student misconceptions and to seek to correct any misconceptions.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 52-53.