B2.10 Identify proportional and non-proportional situations and apply proportional reasoning to solve problems.
Skill: Identifying Proportional and Non-Proportional Situations and Applying Proportional Reasoning
The ability to think and reason proportionally is one essential factor in the development of an individual’s ability to understand and apply mathematics. Susan Lamon estimates that over 90% of students who enter high school cannot reason well enough to learn mathematics and science with understanding and are unprepared for real applications in statistics, biology, geography or physics (Lamon, 2005, p. 10). While students may be able to solve a proportion problem with a memorized procedure, this does not mean that they can think proportionally.
Source: Paying attention to proportional reasoning, 2012, Ontario Ministry of Education, p. 4.
Multiplicative Reasoning
Multiplicative reasoning is a concept that involves reasoning about several ideas or quantities simultaneously. It requires thinking about situations in relative rather than absolute terms. Consider the following problem. If one dog grows from 5 kilograms to 8 kilograms and another dog grows from 3 kg to 6 kg, which dog grew more? When a student is thinking in absolute terms or additively, she/he might answer that both dogs grew by the same amount. When a student is thinking in relative terms, she/he might argue that the second dog grew more since he doubled his previous weight, unlike the first dog who would have needed to be 10 kg to grow by the same relative amount. While both answers are viable, it is the relative (multiplicative thinking) that is necessary for proportional reasoning.
| Representation of reasoning based on absolute values. | Representation of reasoning based on relative values. |
|---|---|
|
The first dog gained 3 kg and so did the second. They gained as much weight as each other.   |
The second dog gained more weight as it doubled its weight, while the first one should have reached 10 kg for a relatively equivalent weight gain. 
Less than doubled its weight 
Doubled its weight |
Why is this important?
Helping students bridge from additive to multiplicative thinking is complex but starts early. It forms the backbone of the mathematics curriculum and includes important and interconnected ideas such as multiplication, division, fractions, decimals, ratios, percentages and linear functions. It requires time, a variety of situations and opportunities to construct their understanding in multiple ways.
Source: Paying attention to proportional reasoning, 2012, Ontario Ministry of Education, p. 5-6.
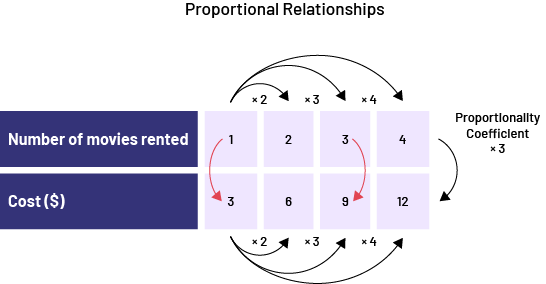
Proportional Relationships
There is a proportional relationship between two quantities when these quantities can increase or decrease simultaneously by the same factor. For example, if one of the two quantities is tripled, the other is also tripled. The ratio between the 2 quantities is then constant (for example, \(\frac{1}{6}\; = \;\frac{3}{{18}}\)). Such equality between two ratios is called a proportion.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 39.
Example
Example 2
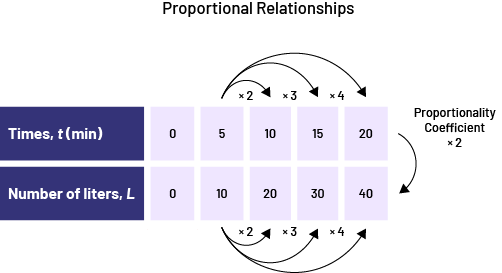
An aquarium, empty at the beginning, fills at a rate of 2 litres of water per minute. Represent, in several ways, the number of litres of water in the aquarium according to time, in minutes.
Visual Representation (Ratio Table)
Graphical Representations
Number of Litres According to Time
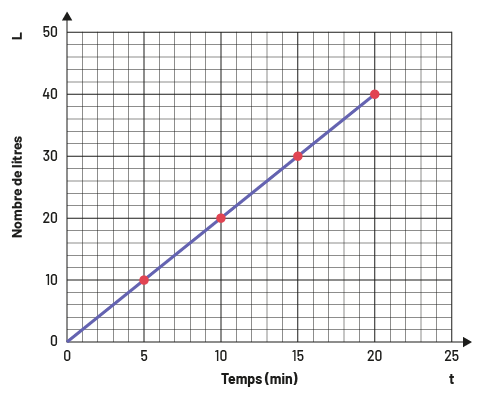
In this situation, the line starts at (0,0) and the student can see from the graph that if the time doubles, the number of litres also doubles.
Situations involving a proportional relationship can be solved intuitively with proportional reasoning.
In the primary grades, students intuitively used proportional reasoning to solve problems involving two quantities that are in a ratio of 1 to many (for example, 1 cake for 8 children), many to 1 (for example, 3 people per table), or many to many (for example, 2 litres of juice for 5 people).
In the junior grades, students were introduced to the terms ratio and proportion, as well as their notation. When two ratios are equivalent, there is a proportion, for example, 2:3 = 10:15 or \(\frac{2}{3}\; = \;\frac{{10}}{{15}}\).
Source: translated from Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 49-51.
A relationship is non-proportional when two variables do not change at the same rate. For example, a deposit of $5 one month and $2 the next is not proportional because the growth is not constant. Its graphical representation would be irregular, not a straight line.
However, some straight lines are considered to be non-proportional relationships.
Example
A plumber charges a customer for a service call and the hours required to repair a problem. She charges $40 for the service call and $30/hour afterwards. The table of values and the graph below represent this situation.
| Number of Hours | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Invoice Amount, $ | 40 | 70 | 100 | 130 | 160 | 190 |
Graph of the invoice amount according to the number of hours worked
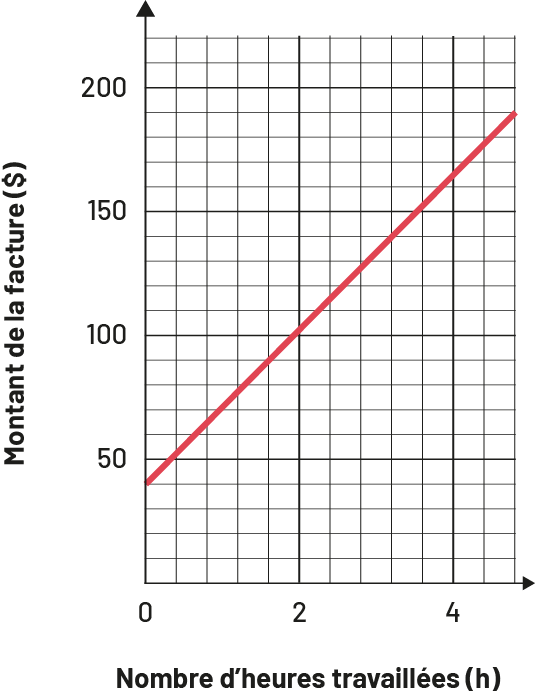
In this situation, the line starts at (0, 40) and the student cannot apply proportional reasoning. This concept is addressed in C1.1.
Beyond the mathematics classroom, proportional reasoning is evident in other subject areas like science, music and geography, as well as in everyday activities. People use proportional reasoning to calculate best buys, taxes and investments, to work with drawings and maps, to perform measurement or monetary currency conversions, to adjust recipes or to create various concentrations of mixtures and solutions.
Source: Paying attention to proportional reasoning, 2012, Ontario Ministry of Education, p. 4.
Example of a problem in which proportional reasoning is used
In the cake recipe, there is (\(\frac{2}{3}\)) of a cup of sugar and 2 cups of flour. How much flour should Mrs. Larose add to the mixture if she has added 3 cups of sugar?
Students can solve this problem using a visual representation such as:

This type of representation shows that the quantity of ingredients in the recipe is increased fivefold if \(3\frac{1}{3}\) cups of sugar are used. However, transposed into a ratio table, the representation has the advantage of helping students to determine a multiplicative relationship between the quantities.

Knowledge: Proportional Reasoning
Students use proportional reasoning early in learning mathematics, for example, seeing that 8 equals \(2\; \times \;4\;{\rm{or}}\;{\rm {4}}\; \times \;{\rm{2}}\) and not just "1 more than 7". Proportional reasoning is used at later stages of learning when the student understands that a speed of 50 km/h is the equivalent of a distance of 25 km traveled in 30 minutes.
Students continue to use proportional reasoning when studying the slope of a curve or derivatives. Proportional reasoning involves looking at numbers in terms of their relative values rather than their absolute values. Students apply proportional reasoning when they determine that a group that grows from 3 to 9 children experiences a greater increase than one that grows from 100 to 150 children because in the first case the number has tripled, while in the second case it has only increased by 50% and has not even doubled.
Activities in the Primary and Junior grades contributed to the development of proportional reasoning. For example, by comparing the value of a set of 4 nickels to the value of a set of 4 pennies, students develop proportional reasoning.
In the Junior and Intermediate Divisions, students work directly with fractions and their use in the context of ratios, rates, and percentages.
Proportional reasoning focuses on relationships and compare quantities or values. As Van De Walle said, "Proportional reasoning is difficult to define. It is not a type of reasoning that one is able to do or not do: it is acquired gradually over time. In particular, it can be described as the ability to think about multiplicative relationships between quantities and to compare such relationships, represented symbolically as ratios." (2008, p. 163) There is sometimes a tendency to believe that proportional reasoning is limited to the study of ratios, rates, and rational numbers such as fractions, decimals, and percents when, in fact, it touches all areas of mathematics. For example, proportionality is an important aspect of measurement, including unit conversion and the dimensional multiplication relationships that exist between area and volume.
Source: translated from Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 49-51.
An example of proportional reasoning in measurement:
Which shape contains the most colour?
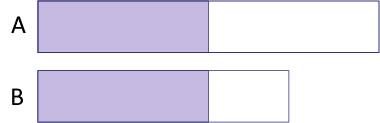
Source: Paying attention to proportional reasoning, 2012, Ontario Ministry of Education, p. 3.
