B2.2 Understand and recall commonly used percents, fractions, and decimal equivalents.
Skill: Understanding and Recalling Commonly Used Percents, Fractions and Decimal Equivalents
We know that a terminating decimal number represents a fraction whose denominator is a power of 10 (for example, \(0.3\; = \frac{3}{{10}}\;\); \(0.47 \;= \frac{{47}}{{100}}\;\)). Because the concept of percent is closely connected to the concept of fractions, there is only one step to take to connect the percent with the decimal number and the decimal fraction. By the intermediate grades, students who have acquired a good sense of number can move from one representation to another without difficulty.
Example
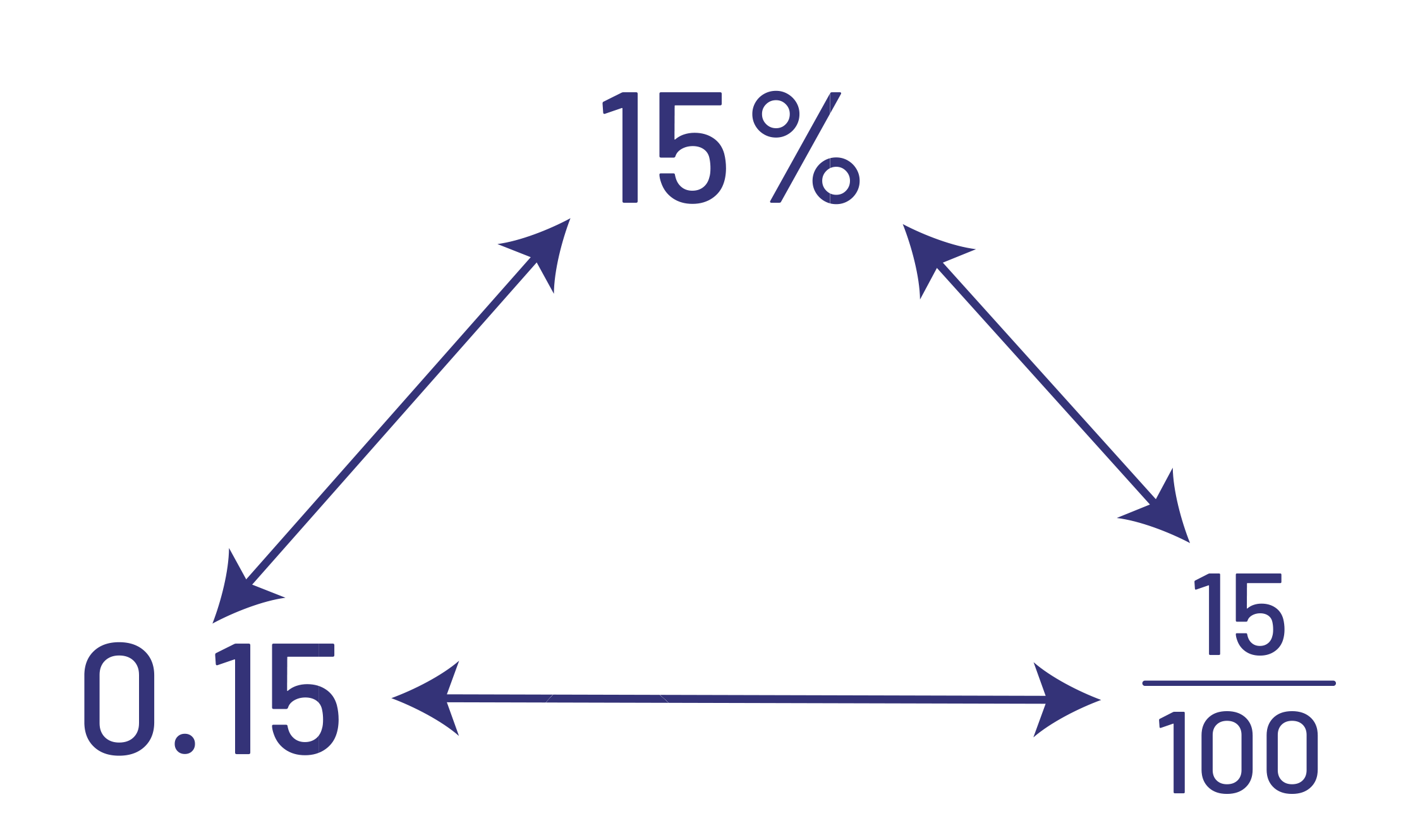
To help students develop this skill, they should be regularly asked to express their answers using another notation. For example, teachers can encourage the student who answered that \(\frac{3}{4}\) of the young people in the class have black hair to also express this answer in decimal notation (0.75) and as a percentage (75%).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 50-51.
Benchmarks
The mental representations used by students are reinforced by the use of benchmarks. In general, a benchmark is a reference point. The benchmarks used in the study of decimals and percents are similar to those used in the study of fractions. By making connections between decimals, percents, and fractional benchmarks, students deepen their number sense.
The table below shows some benchmarks that should be part of the students' knowledge. Any percent can be created using the benchmark percents.
Benchmarks for Fractions, Percents and Decimals
| Fraction | Percent | Decimal Number | Example of a Mental Representation |
|---|---|---|---|
| \(\frac{1}{{100}}\) | 1% | 0.01 |  |
| \(\frac{1}{20}\) | 5% | 0.05 |  |
| \(\frac{1}{10}\) | 10% | 0.1 |  |
| \(\frac{15}{100}\) | 15% | 0.15 |  |
| \(\frac{1}{4}\) | 25% | 0.25 |  |
| \(\frac{1}{2}\) | 50% | 0.5 |  |
These benchmarks, as well as the connections between fractions, percents and decimals, help to deepen number sense and are very useful in problem-solving situations. The ability to switch from one notation to another is advantageous because it allows students to use the one that best meets the needs of the moment. For example, a customer who wants to calculate a 50% discount on the price of an item can easily do so if they recognize that 50% is half \(\frac{1}{2}\).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 38-40.
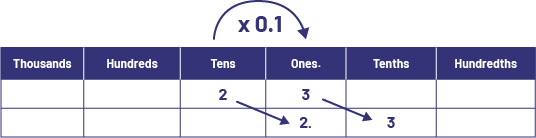
Calculating 1% (or 0.01, one one-hundredth) and 10% (or 0.1, one tenth) of an amount can be calculated mentally by visualizing how the digits of a number change their place value. For example:
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
\(\begin{array}{l}10\% \;{\rm{of \; 23}}\;\\23\; \times \;0.1\; = \;2.3\end{array}\)
I visualize a shift of one column to the right in the place value chart because one tenth of ten is one, and one tenth of 1 is one-tenth, both of which require a shift of one column to the right. It follows that one tenth of twenty is two, and one tenth of 3 is three one-tenths.
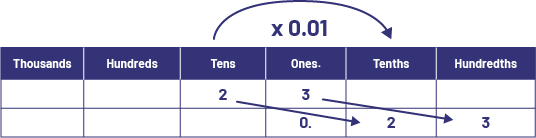
\(\begin{array}{l}1\% \;{\rm{of}}\;{\rm{23}}\\23\; \times \;0.01\; = \; 0.23\end{array}\)
I visualize a shift of two columns to the right in the place value chart because one hundredth of ten is one-tenth, and one hundredth of 1 is one-hundredth. It follows that one hundredth of twenty is two tenths and one hundredth of 3 is three hundredths, both of which require a shift of two columns to the right.
Students often mistakenly believe that a percent cannot exceed 100 (100%). However, there are situations in everyday life that lead to percents greater than 100%. For understanding, these situations can be explored using concrete or visual (semi-concrete) representations where quantities are related to the whole. Fractional or decimal notation can also be used.
Example 1
Following a 25% increase, it can be stated that the new quantity is 125% of the original quantity.
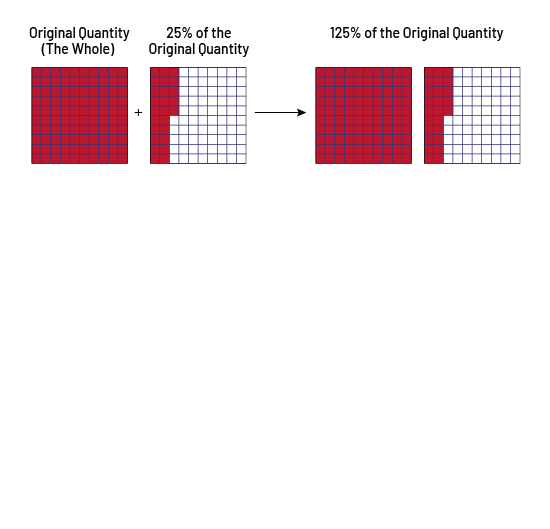
Thus, the new quantity is 125 hundredths of the original quantity or 125% of the original quantity. However, an increase of 125% means that 125% of the whole is added to the original quantity. The new quantity is then 225 hundredths of the original quantity or 225% of the original quantity.
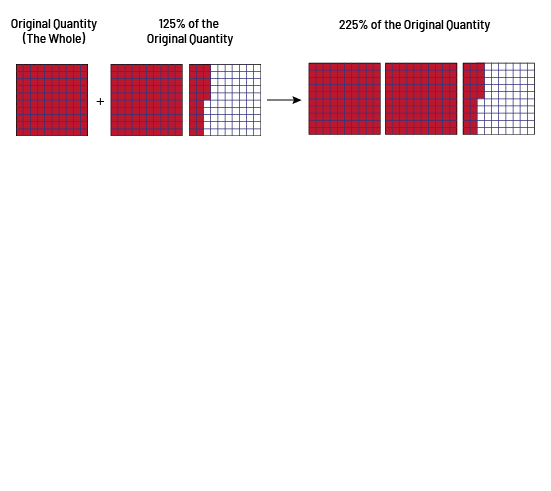
Example 2
During a fundraising event, the students at a local school set a goal of $2000. At the end of the fundraiser, they raised $4 000. What percentage of their goal was raised?
\(\begin{array}{l}100\% \;{\rm{of}}\;{\rm{\$2000}}\;\;{\rm{ = }}\;{\rm{\$2000}}\;\\200\% \;{\rm{of}}\;{\rm{\$2000}}\;\;{\rm{ = }}\;{\rm{\$4000}}\;\end{array}\)
Since 100% of the quantity equals the total quantity, or $2000, then 200% is double that quantity, or $4000.
Knowledge: Decimal Numbers
Decimal numbers are rational numbers with a decimal point. All whole numbers are integers and integers can be expressed as decimal numbers. Fractions can also be expressed as a decimal number that either terminates or repeats.
Example
\(3.72\;{\rm{and}} \; 12.135\;64\)
The set of decimal numbers includes all integers, because integers can be expressed with a decimal part.
Example
\(3\; = \;3.0\)
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 28.
Knowledge: Fractions
The word fraction comes from the Latin fractio which means "break". In order to determine a fraction of a whole that has been divided into parts, the parts must be of equal or equivalent size. Note that when we talk about equivalent parts, we are not necessarily talking about identical shapes, although these are easier to use. The representations of 1 fourth \(\frac{1}{4}\) in the example below are based on the area of the whole. Since each whole has an area of 16 square units, each fourth has an area of 4 square units. Despite their different shapes, each of these fourths represents an equivalent part of the same whole.
Example
Six equivalent representations of 1 fourth (\(\frac{1}{4}\)) of the same whole.

It is important for students to understand that the more the whole is broken up, the smaller its parts are
Example

The fourths of a whole are bigger than the tenths of the same whole.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 33.
Knowledge: Percent
Percent is a special way of presenting a fraction. It is often used in everyday life. A numerical expression such as 30% (which reads "30 percent") is actually another representation of the number 30 hundredths, or 0.30. To facilitate understanding of the concept of percent, students should first make the connection between percent and the fraction with a denominator of 100, using concrete or visual (semi-concrete) materials.
Example
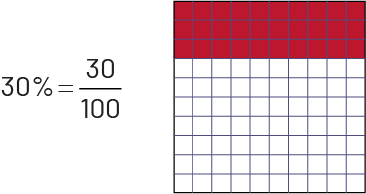
Students should also realize that a percent represents a ratio to 100 (for example, 30% is the ratio of 30:100). It is important to note that a result expressed as a percent does not mean that the quantity in question is necessarily composed of 100 parts, as explained in the following table.
| Representation | Percent | Instructional notes |
|---|---|---|
 
|
75% of the circles are green. | Even if 75% of the circles are green, it does not mean that there are 100 circles in the whole. However, if there were 100 circles, there would be 75 green circles. Also, the fraction of circles that are green is equivalent to \(\frac{{75}}{{100}}\)(for example, \(\frac{3}{4}\; = \;\frac{75}{{100}}\) and if this amount were doubled the corresponding fraction would be: \(\frac{{150}}{{200}}\; = \;\frac{75}{100}\). |

|
50% of the land is covered with grass. | Even if 50% of the field is covered with grass, it does not mean that the field has an area of 100 m2. The entire field is 4000 m2. If half of it is covered with grass, there would be 2000 m2 of grass. Thus, \(\frac{{2000}}{{4000}}\; = \;\frac{1}{2}\; = \;\frac{{50}}{{100}}\; = \;50\% \). |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 34-35.
