B2.3 Use mental math strategies to increase and decrease a whole number by 1%, 5%, 10%, 25%, 50%, and 100%, and explain the strategies used.
Skill: Using Mental Math Strategies to Increase and Decrease a Whole Number by 1%, 5%, 10%, 25%, 50%, and 100%
Mental Representation
Students need to be able to create a mental representation of a percent, as they do with decimal numbers. The very nature of a percent makes it easier for them to visualize a quantity, as it is always a ratio to 100. It should also be understood that a percent is another way of representing a quantity.
Example

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 37.
Benchmarks
The mental representations used by students are reinforced by the use of benchmarks. In general, a benchmark is a reference point. The benchmarks used in the study of decimals and percents are similar to those used in the study of fractions. By making connections between decimals, percents, and fractional benchmarks, students deepen their number sense.
The following table provides some benchmarks that should be part of the students' knowledge.
Benchmarks for Fractions, Percents and Decimals
| Fraction | Percent | Decimal Number | Example of a Mental Representation |
|---|---|---|---|
| \(\frac{1}{{100}}\) | 1% | 0.01 |  |
| \(\frac{1}{20}\) | 5% | 0.05 |  |
| \(\frac{1}{10}\) | 10% | 0.1 |  |
| \(\frac{15}{100}\) | 15% | 0.15 |  |
| \(\frac{1}{4}\) | 25% | 0.25 | 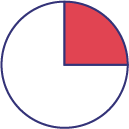 |
| \(\frac{1}{2}\) | 50% | 0.5 |  |
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 39.
Mental Math
Everyday life presents many opportunities to perform operations with percents. For example, provincial sales tax on purchases are calculated using percents and sports data are often presented using percents. Estimation and mental math skills are characteristics of good number and operation sense. A variety of mental math strategies can be used including rounding, decomposing, and the use of benchmarks. Some examples of their using in mental math include:
Decomposing and Rounding to Approximate Using Benchmarks
Example 1
Abdul buys a salad and juice for his lunch. The cost is $9 plus 13% sales tax. Approximately how much will Abdul's lunch cost?
To find out the approximate cost of his dinner, Abdul can:
- Round up to the nearest benchmark percentage (15%); the student can decompose the 15% into 10% and 5% (half of the 10%) and then calculate the amounts 10% of $9 + 5% of $9 (half of the 10%) = 90¢ + $0.45 = $1.35.
- Add up the cost and tax ($9 + $1.35 = $10.35).
*Rounding up the sales tax gives Abdul an approximate total for his dinner.
Example 2
A manager purchases a machine at a 25% discount. The machine costs $184. How much money will the manager save?
The total cost will go down because there is a discount.
Decompose 184 (100 + 80 + 4 + 1).
Equivalence: \(\ \;25\% = \frac{1}{4}\).
Calculation
25% or one fourth of $100 is $25
25% or one fourth of $80 is $20
25% or one fourth of $4 is $1
The manager will save $25 + $20 + $1 = $46.
Use of Benchmarks
Example
Over the past 10 years, the school has seen a 30% decrease in student enrollment. If there were 800 students enrolled 10 years ago, how many students are currently enrolled?
A decrease leads to a subtraction; the number of students will be lower.
Decompose the 30% using benchmarks (example: \(25\% \; + \;5\% \)).
25% is a fourth of the total, so divide \(\frac{{800}}{4}\; = \;200\) students.
5% is half of 10%, so \(10\%\; = \;\frac{1}{{10}}\), divide 800 by 10 = 80 students and divide 80 students by 2 to get the 5% which is equivalent to 40 students.
Therefore, there is a decrease of 240 students which means that there are now 560 students enrolled.
Use the Place Value
Example
One store reports that its average daily sales are up 10% from last week. Last week's average sales were $1250. What is this week's average sales?
Increased sales, so the value will be greater:
- The $1250 is the whole and the addition is 10% of it.
- 10% is equal to 0.1.
- To calculate the addition (10% more): decompose 1250 (1000 + 100 + 100 + 50).
- 0.1 of 1000 is 100 (another option: \(0.1\;=\;\frac{1}{{10}}\), so divide the amount by 10).
- 0.1 of 100 is 10 (2 times).
- 0.1 of 50 (half of 100) is 5.
The extra 10% equals $125 so the sales amount is $1375.
Knowledge: Percent
Percent is a special way of presenting a fraction. It is often used in everyday life. A numerical expression such as 30% (which reads "30 percent") is actually another representation of the number 30 hundredths, or 0.30. To facilitate understanding of the concept of percent, students should first make the connection between percent and the fraction with a denominator of 100, using concrete or visual (semi-concrete) materials.
Example
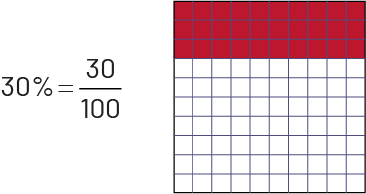
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 34.
Knowledge: Mental Math
Most everyday calculations are related to mental math. People who develop good mental math skills do not rely on electronics or paper to perform everyday calculations. Yet, it is important to demystify mental math. "Mental math is the ability to perform calculations with little or no help from a pencil and paper or a calculator. It represents an essential component of effective instruction." (Ontario Ministry of Education, 2004 a, p. 24) Thus, it is not about using an algorithm in one's head, but about calculating flexibly and efficiently.
Depending on the situation, mental math is used to determine approximate or exact results. We often estimate mentally when we are looking for an order of magnitude. For example, to get an idea of the tax cost of one's purchases, one uses simpler numbers. It is also important to be able to calculate mentally with precision (for example, a waiter who must give change to a customer). Many mental math strategies are based on the relationships between the whole and its parts (composing, decomposing, and recomposing), the relationships between and among numbers and their various representations and the relationships between operations and their properties. Often, these strategies come from a transfer of models used during operations learning.
Example
Round up:
1.2% of 100
1% of 100 is 1
1.2% of 100 is just over 1
Using benchmarks:
23% of 400
25% of 400 is 100
23% of 400 is just under 100
Using the place value of the digits:
10% of $500
10% = 0.1
0.1 of 500 is 50
Decomposing numbers:
50% of 355
50% of 300 = 150
50% of 50 = 25
50% of 5 = 2.5
\(150\; + \;25\; + \;2.5\; = \;177.5\)
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 111-112.
