B2.4 Use objects, diagrams, and equations to represent, describe, and solve situations involving addition and subtraction of integers.
Skill: Representing, Describing and Solving Addition and Subtraction of Integers
In Grade 7 , students will add and subtract integers using a variety of representations (two different colours of counters, number line) and computational strategies that will support them generalizing computational rules. The use of two colours of counters and the number line is essential to illustrate addition and subtraction of integers. By using these models, students create visual representations of the operations being performed and develop a better understanding of the rationale for the different rules that govern addition and subtraction of integers. Rather than teaching rules, it is better for the student to be able to generalize them as a result of their observations. The rules for integer computation are the end point, not the beginning point, of teaching and learning about integers.
Source: translated from Les mathématiques…un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 7e année, Module 3, Série 1, p. 15.
As with whole numbers, the addition of integers is commutative. So the order in which the integers are written in an addition is not important.
However, as with whole numbers, the commutative property does not apply to subtraction. The order in which the integers are written in a subtraction is important.
When writing an equation, integers are often placed inside brackets and the equation written as \(( \; + 3)\; - \;(\; - 2)\; = \;(\; + 5)\).
- If an integer sign is not included, the number is considered positive.
- These conventions help reduce confusion between the number and the operation.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Coloured counters model (2 different colours)
One colour represents positive numbers and another represents negative numbers.
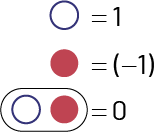
In this model, two counters of opposite colours add to 0. These are “Zero pairs” where the sum of a positive and a negative number results in zero.
Examples
\( - 5\; + \; + 3\)
I represented the integers with 5 red and 3 white counters.
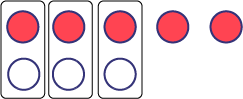
I combined 1 red counter with 1 white counter to create zero pairs since their value is 0. In all, there are 3 zero pairs. The remaining counters represent the integer (-2). So, \( - 5\; + \; + 3\; = \; - 2\).
\( - 5\; + \; - 3\)
I represented each term with coloured counters, that is 5 red and 3 red counters.

In total, there are 8 red counters. This set of counters represents the integer -8. Then, \( - 5; + \; - 3; = \; - 8\).
\(5\; - \; + 3\)
I represented each term with coloured counters. I have 5 white counters and 3 red counters.
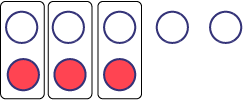
I combined red counters with white counters to create zero pairs. In all, there are three zero pairs. The remaining counters represent the integer 2. So, \(5\; + \; - 3\; = \; + 2\;\;{\rm{or \;\;2}}\).
\(5\; - \;( - 3)\)
I represented 5 with five white counters.

I have to remove 3 but I don’t have −3 to remove, so I add three zero pairs.

Now I can remove 3.

This leaves me with +8.

The remaining counters represent the integer 8. Then, \((- 5)\; + \;(- 3)\; = \;(- 8)\).
Number Line Model
In this model, integers are represented by arrows. The direction of the arrow determines whether the value represents a positive or negative quantity. The length of the arrow represents the quantity, and its direction, the sign.
Example
\( + 8\; + \; - 5 = \; + 3 \)

The black arrow that is positive (points to the right) represents 8.
The red arrow that is negative (points to the left) represents -5.
Then, \( 8\; + \;(- 5) = \; 3 \).
When two positive integers are added together, the result is positive. This can be visualized on a number line as:
- two arrows moving in a positive direction (to the right or up);
- one arrow moving in a positive direction from a positive starting position.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Example
\(20\; + \;60 = \;80\)
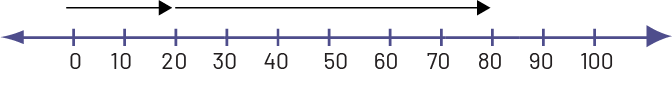
From 0, the student jumps 20 and then adds a jump of 60 so the final position is the sum that equals 80. So, \(60\; + \;20\; = \;80\).
When two negative integers are added together, the result is negative. This can be visualized on a number line as:
- two arrows moving in a negative direction (left or down);
- one arrow moving in a negative direction from a negative starting position.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Example
\(( - 2)\; + \;( - 5)\)

From 0, the student draws a red arrow that goes 2 units to the left. From -2, they move another 5 units to the left. The student stops at -7. Then, \((- 2)\; + \;(- 5)\; = \;(- 7)\)
When a positive and a negative integer are added together, the result is negative if the absolute value of the negative integer is greater than the absolute value of the positive integer. This can be visualized on a number line as:
- one arrow moving right in a positive direction and the other arrow of greater magnitude moving left in a negative direction;
- one arrow moving left in a negative direction starting from a positive integer and ending below zero;
- one arrow moving right in a positive direction starting from a negative integer and ending below zero.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Example
\(\ ( - 6) + (4) \)
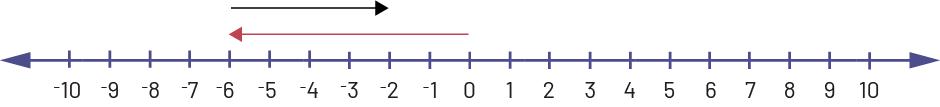
From 0, the student draws an arrow moving left to −6. Then, from -6, they draw an arrow going to the right 4 units. The arrow stops at -2.
Then, \(( - 6)\; + \;(4)\; = \; - 2\)
When a positive and a negative integer are added together, the result is positive if the absolute value of the positive integer is greater than the absolute value of the negative integer. This can be visualized on a number line as:
- one arrow moving left in a negative direction and the other vector of greater magnitude moving right in a positive direction;
- one arrow moving right in a positive direction from a negative integer and ending above zero;
- one arrow moving left in a negative direction from a positive integer and ending above zero.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Example
\(\ ( - 3) + (7)\)

From 0, the student draws a red arrow going 3 units to the left. From -3, they draw a black arrow going 7 units to the right. The arrow stops at 4. Then, \(( - 3)\; + \;(7)\; = \;4\).
The subtraction on the number line can also be seen as the difference between the two numbers.
Example
\((5)\; - \;( - 3)\; = \;8\)
\(5; - \;( - 3)\) means the difference between -3 and 5

Familiar real-world contexts for negative and positive integers (for example, temperature, elevators going up and down, parking garages, sea level, golf scores, plus/minus in hockey, gaining and losing money, walking forward and backwards) provide a starting point for understanding adding and subtracting with integers.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Example 1

According to the weather report, it is currently -4°C in Iqaluit. The temperature will rise by 9 degrees during the day. What is the maximum temperature expected?
An example of a possible solution is:
I know that 5°C is 9 degrees warmer than -4°C.
Therefore, the maximum temperature expected in Iqaluit is 5°C.
Source: translated from Les mathématiques…un peu, beaucoup, à la folie!, Guide pédagogique, Numération et Sens du nombre/Mesure, 7e année, Module 3, Série 1, p. 81.
Example 2
In the spring, Patrick borrows $75 from his parents to buy a bike. Over the summer, he saves up to pay his parents back. In September, he gives his parents $25. In October, he gives them $30. What is Patrick's financial situation as a result of his loan?
Examples of possible solutions include:
Debt: $75 or $-75
Money saved: \((\$25 + \;\$30)\; \text{or} \;\$55\)
Patrick paid back $55 of the $75 he owed his parents.
\(\begin{align}(- 75)\; + \; 25\; + \; 30\; &= \;(- 75)\; + \; 55\\ &= ((- 20)\; + \;(- 55))\; + \; 55\\ &= (- 20)\; + \;0\\ &= (- 20)\end{align}\)
Patrick still owes his parents $20.
Source: translated from Les mathématiques…un peu, beaucoup, à la folie!, Guide pédagogique, Numération et Sens du nombre/Mesure, 7e année, Module 3, Série 1, p. 78.
Knowledge: Integers
The integers belong to the set ℤ.
ℤ = {…, -3, -2, -1, 0, 1, 2, 3,…}
Each integer consists of a number and a sign (– or +).
Every integer has an opposite (for example, -3 and 3). The opposite of a positive number is a negative number of the same quantity (absolute value), and vice versa.
The signs - and + are associated with a number. They are not operation signs. Thus, the number -4 reads: negative 4.
There is no space between the negative sign - and the number 4, since it is not the subtraction operation.
0 is neither a positive nor a negative number. It is the only number that is its own opposite.
On the number line, the numbers are in ascending order from left to right and descending order from right to left.
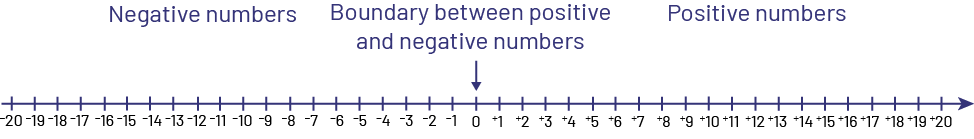
Source: translated from Les mathématiques…un peu, beaucoup, à la folie!, Guide pédagogique, Numération et Sens du nombre/Mesure, 7e année, Module 3, Série 1, p. 35-37.
