B2.6 Determine the greatest common factor for a variety of whole numbers up to 144 and the lowest common multiple for two and three whole numbers.
Skill: Determining the Greatest Common Factor (GCF) for a Variety of Whole Numbers up to 144 and the Lowest Common Multiple (LCM) for 2 or 3 Whole Numbers
The ability to recognize whether a number is prime or composite, whether it is even or odd, or whether it is divisible by any number can make it easier for students to use various strategies to find the lowest common multiple or greatest common factor of whole numbers.
Multiple of a Number
A multiple of a whole number corresponds to the product of this number by another whole number. For example, the number 12 is a multiple of 4 because \(12\; = \;4\; \times \;3\). It is also a multiple of 1 (\(12\; = \;1\; \times \;12\)), of 2 (\(12\; = \;2\; \times \;6\)) , 3 (\(12\; = \;3\; \times \;4\)), 6 (\(12\; = \;6\; \times \;2\)) and 12 ( \(12\; = \;12\; \times \;1\)). Students should be able to determine whether or not a number is a multiple of another number (for example, “Is 42 a multiple of 7?”). They must also be able to list multiples of any number (for example, multiples of 7 are: 7, 14, 21, 28, 35, 42, 49…). The list of multiples of a number is endless. The important thing is therefore not to know a partial list of these multiples by heart, but to be able to produce one if necessary.
Note: According to the definition of a multiple of a number, the number 0 is a multiple of every whole number. For example, 0 is a multiple of 7 since \(7 \times \;0\; = \;0\). However, this special case is not usually included when asked to list the multiples of any whole number. In many situations, it is useful to identify a multiple that is common to two numbers. The search for such a common multiple, which usually involves comparing lists of multiples of each of the two numbers, should be done in a problem-solving context.
Example
One student rings a bell every 6 seconds and one student whistles every 8 seconds.
a) When will they make their sounds at the same time for the first time?
b) At what other times will the sounds coincide?
To solve this problem, students can construct a table of values or write a list of multiples of 6 (6, 12, 18, 24…) and 8 (8, 16, 24, 32…). They will then be able to determine that the 2 students will produce their sounds at the same time for the 1st time at the 24th second. This is the lowest common multiple (LCM).
| Number of Sounds | 1 | 2 | 3 | 4 | … |
|---|---|---|---|---|---|
|
Bell Sound |
6 | 12 | 18 | 24 | |
|
Whistling sound |
8 | 16 | 24 | 32 |
To answer the second question, they must determine the next common multiples of 6 and 8, that is., 48, 72, 96… Although the concept of lowest common multiple (LCM) is not taught until Grade 7, many algebra problems in the junior grades involve finding a common multiple of two numbers.
Factor and Divisor of a Number
In a multiplication of two or more whole numbers, each of these numbers is called a factor of the number that is the product. For example, 2 and 8 are factors of 16.

Note: If we want to list all whole numbers that are factors of 16, we need to also include 1, 4 and 16 since \(1\;\times\;16\;=\;16\;\text{and}\;4\;\times\;4\;=\;16\).
In division, the relationship between the dividend and the divisor results in a quotient. A whole number is said to be a divisor of another whole number if their quotient is a whole number. Thus, 3 is a divisor of 21 since the quotient is 7 which is a whole number.
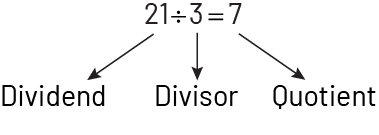
Note: If we want to list all the possible divisors of 21, we need to also include 1, 7, and 21 since \(21\;\div\;1\;=\;21\;\text{,}\;21\;\div\;7\;=\;3,\;\text{and}\;21\;\div\;21\;=\;1\). Students should understand that any whole number has at least two divisors, the number itself and the number 1.
Since multiplication and division are inverse operations, it is possible to establish relationships between the concepts of multiple, factor, dividend, divisor and quotient.
For example, any factor of a number is also a divisor of that number (4 is both a factor and a divisor of 28). Thus, the relationships between numbers can be expressed differently depending on the analysis of a given situation. For example, students might say that 8 is a multiple of 4, that 4 is a factor of 8, that 8 is divisible by 4, or that 4 is a divisor of 8.
They could also recognize that the number 24 is a multiple of the set of numbers {1, 2, 3, 4, 6, 8, 12 and 24} and that these numbers are its factors or divisors.
Some situations involve finding a common divisor of two numbers. This search, like the search for common multiples, should be done in a problem-solving context.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 56-58.
Greatest Common Factor (GCF)
Students will use strategies to find the greatest common factor (GCF) to be efficient when simplifying a fraction.
Example
Simplify the fraction \(\frac{{36}}{{54}}\).
Strategy:
To simplify this fraction, the student finds the GCF of 36 and 54.
They find all the factor combinations that result in 36 and 54. Suggest that they start with 1.
For example, the student might ask: 1 times what number is 36 or 36 divided by 1 is what number? Continue with 2 and so on.

The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
The factors of 54 are 1, 2, 3, 6, 9, 18, 27, 54.
Therefore, the student chooses the greatest factor of the two lists.
The GCF is 18.
The student can now simplify the fraction to its lowest terms.
\(\frac{{36 \div \;18}}{{54 \div \;18}}; = \;\frac{2}{3} \)
The student divides the numerator and denominator by the GCF.
Example
Mr. Theis has 36 red pens and 120 blue pens. He wants to divide all these pens into packets of red pens and packets of blue pens. He also wants to make sure that the number of pens in the blue pen packets is the same as in the red pen packets.
a) How many pens can he put in each packet?
b) What is the greatest number of pens he can put in each packet?
To solve this problem, students can list the possible factors of 36 and 120.

By comparing the lists and deciding that 1 pen is not a packet, they will be able to see that Mr. Theis can make packets of 2, 3, 4, 6, or 12 pens and that 12 is the most pens he can put in a packet.
12 is therefore the greatest common factor (GCF).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 58.
Lowest Common Multiple (LCM)
The student must know the lowest common multiple (LCM) in order to add and subtract fractions without a common denominator. The student finds equivalent fractions in order to perform the calculations. In this case, the lowest common multiple is determined for all denominators.
Example
\(\frac{5}{{12}}\; + \;\frac{1}{18}\; = \;?\)
Possible strategies:
The student finds the LCM of 12 and 18 in order to have a common denominator.
- The student finds the multiples of 12 and 18, stopping when the first common multiple is identified.
Therefore, the LCM of 12 and 18 is 36.
- The student finds all the prime factors of the 2 numbers using factor trees.
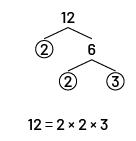
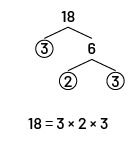
Thereafter to find the LCM, the student identifies the prime factors that are common to the 2 numbers (crossed out below). Then, they identify the remaining prime factors.
Common prime factors of the 2 numbers: 2 and 3

Prime factors remaining to the 2 numbers: 2 and 3
Thus, the LCM is the product of the multiplication of the common prime factors by the remaining prime factors.
LCM: \((2\; \times \;3)\; \times \;(2\; \times \;3)\; = \;36\)
The student can now continue with the addition of the 2 fractions with a common denominator of 36.
\(\frac{5}{12}\; + \;\frac{1}{{18}}\; = \;\frac{5\; \times \;3}{12\; \times \;3}\; + \;\frac{1\; \times \;2}{18\; \times \;2}\; = \;\frac{15}{36}\; + \;\frac{2}{36}\; = \;\frac{17}{36}\)
Knowledge: Multiple
A number which is the product of a given whole number multiplied by any other whole number. For example, some multiples of 4 are 4, 8, 12, 16, and 20 (4 × 1, 4 × 2, 4 × 3, 4 × 4, 4 × 5).
Knowledge: Lowest Common Multiple (LCM)
The smallest number that two numbers can divide into evenly. For example, 60 is the lowest common multiple of 10 and 12.

Knowledge: Factor
Natural numbers that divide evenly into a given natural number.
Example
The factors of 12 are 1, 2, 3, 4, 6 and 12.
Note: Generally, the factors of a number are whole numbers. Since multiplication and division are inverse operations, it is possible to establish relationships between the concepts of multiple, factor, dividend, divisor and quotient. For example, any factor of a number is also a divisor of that number (4 is both a factor and a divisor of 28).
Knowledge: Prime Factor
Factor that is a prime number in the factorization of a number. For example, \(90\; = \;2\; \times \;3\; \times \;3\; \times \;5\).
The prime factors of the number 90 are 2, 3 and 5.
Knowledge: Factor Tree
A diagram drawn to find the factors of a natural number.
Example

Knowledge: Divisor
Name given to a whole number that divides another.
Example The divisors of 6 are 1, 2, 3 and 6.
Note: Generally, the divisors of a number are positive integers. Since multiplication and division are inverse operations, it is possible to establish relationships between the concepts of multiple, factor, dividend, divisor and quotient. For example, any factor of a number is also a divisor of that number (4 is both a factor and a divisor of 28).
Source: translated from En avant les maths! 7e, Nombres, p. 2.
