At a Glance...

B2.9 Multiply and divide decimal numbers by decimal numbers, in various contexts.

Skill: Multiplying and Dividing Decimal Numbers by Decimal Numbers in Various Contexts

---

Multiplication

Junior students already have experience with the concept of multiplication and understand that multiplication of whole numbers results in a product that is greater than the quantities involved, except in situations involving multiplication by 1 and by 0.

In Grade 5, they are often surprised to find that a multiplication in which one of the factors is a decimal number less than 1 gives a product less than the other factor (for example, \(10\; \times \;0.5\; = \;5\); \(20\; \times \;0.1\; = \;2\)).

These results are surprising to anyone who does not deal with numbers in context or has not developed an understanding of multiplication to explain such results.

Example

If students have to determine the distance traveled by a rabbit which makes 8 jumps of 0.5 m, they are confronted with a multiplication which gives a product less than the factor 8, because \(0.5\; \times \; 8\; = \;4\) (the rabbit jumped 0.5 m 8 times). To evaluate the expression \(0.5\; \times \;8\), we can use a number line and represent the 8 jumps. This results in a total distance of 4 m.

While it may seem surprising that the product is less than a factor of 8, the context allows students to understand why. Students then develop a better understanding of multiplication that accounts for such situations.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 79.

In general, there are 2 ways to interpret a multiplication written symbolically, for example \(3 \times 4\). It can be interpreted as 3 times the number 4, which is equivalent to 3 groups of 4, or as the number 3 multiplied by 4, which is equivalent to 4 groups of 3. According to Baruk (1995, p. 737), an expression such as the number 3 multiplied by 4 is "cumbersome and not very consistent with the natural expression in the language of a repeating quantity". In this resource, the expression \(3 \times 4\) will be interpreted as 3 times the number 4 or 3 groups of 4 in order to respect the most natural meaning.

If the students understand that \(3 \times 4\) means 3 groups of 4, they will be able to understand the meaning of \(8 \times 0.5\), that is 8 groups of 0.5 as shown in the following illustration in which a flat represents the unit.

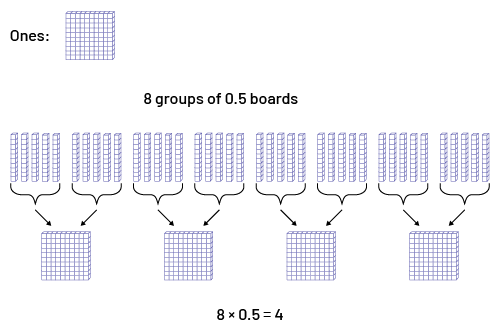
When you multiply a whole number by 0.1 the value becomes one tenth as large, which is the same as dividing it by 10.

When you multiply a whole number by 0.01, the value becomes one one hundredth as large, which is the same as dividing it by 100.

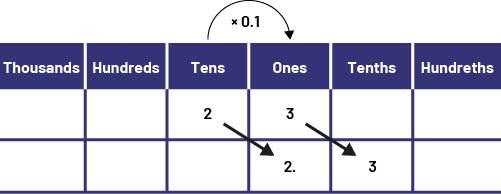
• Multiplication performed using the place value chart

\(23\; \times \;0.1\; = \;2.3\)

I visualize a shift of 1 column to the right in the place value chart.

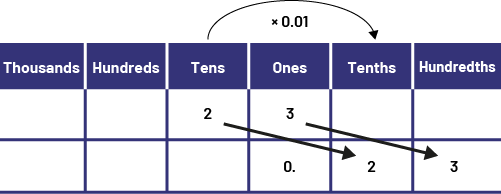
\(23\; \times \;0.01\; = \;0.23\)

I visualize a shift of 2 columns to the right in the place value chart.

At the outset, it's very important to understand one element of number sense: the order-of-magnitude relationship between 2 numbers made up of the same digits in the same order. This relationship can be recognized by observing the position of the decimal point in numbers.

Example

This understanding makes it unnecessary to learn rules like “when you multiply by 10, you push the decimal one place to the right”. Instead, students can analyze the situation of a multiplication where one of the factors is a decimal. For example, they may discover that the products of \(2 \times 12\) of \(2 \times 1.2\) of \(2 \times 0.12\) and of \(2 \times 0.012\) are related. In these expressions, the digits 1 and 2 appear together in the same order in one of the factors. Similarly, the numbers 2 and 4 appear together in the same order in the product. Students could explain this relationship as follows:

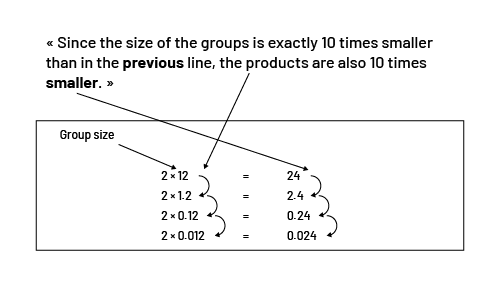
The following table demonstrates this same relationship using concrete representations.

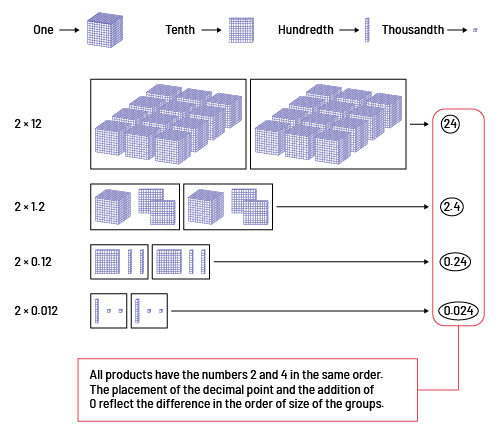
For example, when students understand the relationship between the factors 12, 1.2, 0.12, and 0.012, that is, each is 10 times smaller than the previous one, and the effect of this relationship on the product, they understand why it is possible to multiply decimal numbers as if they were whole numbers and then position the decimal point based on estimation and knowledge of the order of magnitude. As the examples above demonstrate, students learn to determine the position of the decimal point in the product by developing and using their number sense, not by learning one more rule. The following are examples of using estimation to determine the position of the decimal point in a product.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 81-83.

In Grade 6, students multiply a 3-digit whole number by a decimal number up to tenths.

In traditional decimal multiplication teaching, an algorithm is taught. For example, to perform \(0.1 \times 125\), first proceed as for whole numbers:

\(\begin{array}{l}\quad 125\\\underline { \times \;\;0.1} \\\;\;\;\;125\end{array}\)

Then, we count the number of decimal places in the 2 factors (1 in this example) and place the decimal point in the product so that it has the same number of decimal places. We then get:

\(\begin{array}{l}\quad 125\\\underline { \times \;\;0.1} \\\;\;\;12.5\end{array}\)

For students, it is just another rule to learn, which reinforces their impression that learning mathematics is about learning to obey a multitude of rules. The importance of learning this rule has diminished with the advent of the calculator. It is more important for students to integrate the specifics of decimal multiplication with their knowledge of whole number multiplication and to develop their number sense and sense of operations so that they can predict the order of magnitude of the product of 2 given numbers.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 80-81.

When students represent the multiplication of a whole number by a decimal number in a concrete or semi-concrete way (for example, using base ten materials, a number line, an area model), they better grasp the meaning of multiplication. The strategies for multiplying decimal numbers are essentially the same as those used for multiplying whole numbers. Here are different strategies for multiplying a decimal number by a whole number.

Example

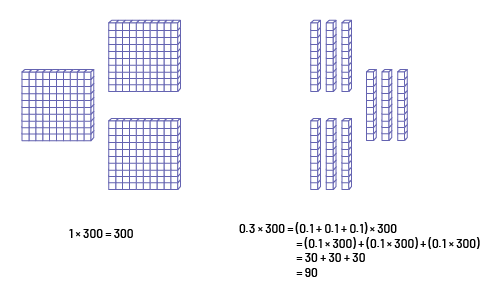
\(1.3\; \times \;300\)

In order to estimate the product, it is possible to reason as follows: 1.3 is between 1 and 2 so \(1.3\; \times \;300\), it's between \(300\;\;\;(300\; \times \;1)\) and \(600\;\;\;(300\; \times 2)\). There is a little more than a group of 300.

• Multiplication using base ten material

I decompose 1.3 into \(1\; + \;0.3\). I multiply \(1\; \times \;300\).

Then I decompose 0.3 down into \(0.1\; + \;0.1\; + \;0.1\) since I know that 0.1 of 300 is 30. So I add \( 30\;+\;30\;+\;30\;=\;90\).

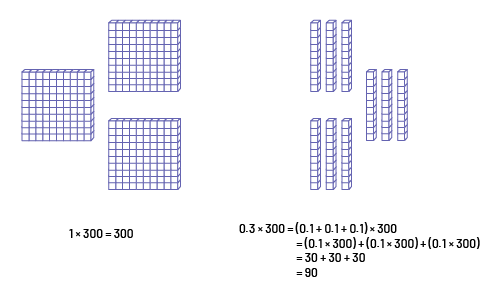
• Multiplication using an area model

I have decomposed the 2 factors, 1.3 into \(1\; + \;0.3\) for rows and 300 into \(100\; + \;100\; + \;100\) for columns.

I multiplied each hundred by one (\(100\; + \;100\; + \;100\)).

Then I multiplied each hundred by 0.3 (\(30\; + \;30\; + \;30\)).

\(300\; + \;90\; = \;390\).

• Multiplication using a number line

• Multiplication using a personal algorithm

Example

The calculations are made starting from the left and according to the place value.

• Multiplication using the standard algorithm

Note: In the case of the standard algorithm, it is important that students do not learn a procedure by heart, but that they understand each step of the procedure and can explain it and associate it with a concrete or semi-concrete representation.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 104-107.

In Grade 7, students will multiply a decimal number by another decimal number. With more experiences with multiplying and dividing decimals, they will become more selective in their choice of problem-solving strategy, represent their calculations in a more structured manner, and adopt increasingly efficient approaches.

Since students have already developed and used several personal algorithms involving whole numbers and decimal tenths, they will be able to make connections between those strategies and working with a greater variety of decimal numbers. 

Source: ranslated from Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Numération et Sens du nombre/Mesure, 8^e, Module 2, Série 1, p. 16-17.

Example

\(16.5\; \times \;1.5\)

• Multiplication performed using the area model

I used the distributive property to decompose 16.5 and 1.5 into (\(16\; + \;0.5\)) and (\(1\; + \;0.5\)). I divided the rectangle into rows and columns and represented the partial products.

To find the product, I add all the partial products.

\(16\; + \;8\; + \;0.5\; + \;0.25\; = \;24.75\)

\(16.5\; \times \;1.5\; = \;24.75\)

• Multiplication performed with the standard algorithm

Note that the standard multiplication algorithms for whole numbers can be applied to decimal numbers. As with whole numbers, these algorithms add partial products to create a total.

Estimation

\(\begin{array}{l}{\rm{1}}{\rm{.5 \ is \ between \ 1 \ and \ 2}}\\16.5\; \times \;1.5\;{\rm{is \ between \ 16 \ and \ 32}}{\rm{, \ since \ 16}}\; \times \;{\rm{1}}\;{\rm{ = }}\;{\rm{16 \ and \ 16}}\; \times \;{\rm{2}}\;{\rm{ = }}\;{\rm{32}}{\rm{.}} \end{array}\)

A "good" estimation helps to check the reasonableness of the product and helps us to know where to place the decimal point.

• Multiplication performed with the help of relocation

One strategy for multiplying decimal numbers is to decompose them to be the products of whole numbers multiplied by 10, 100, or 1000. When the product is obtained, compensate by dividing by the same factor of ten that was used previously.

I multiply 16.5 by 10 and 1.5 by 10 to relocate the decimal point.

\((16.5\; \times \;10)\; \times \;(1.5\; \times \;10)\; = \;165\; \times \;15\)

I multiplied whole numbers \(165 \times 15\).

\(\begin{array}{r}\;165\\\underline { \times \;15} \\\;25\\\;300\\\;500\\\;50\\\;600\\\underline { + \;1000} \\\;\;2475\end{array}\)

When the product of the whole numbers is obtained, to maintain the equivalence, it is necessary to divide the product by \(100\;(10\; \times \;10)\) since we had multiplied each factor by 10 (compensation strategy).

\(2475\; \div \;100\; = \;24.75\)

Therefore, \(16.5\; \times \;1.5\; = \;24.75\)

Note: Initially, if the student has estimated that the number is between 16 and 32, they may deduce that the decimal point is placed between the 4 and 7.

• Multiplication performed with an equivalent multiplication

A strategy to multiply decimal numbers is to decompose them as a product of whole numbers with tenths, hundredths, or thousandths and then apply the associative property.

Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.

\(\begin{align}16.5 \times \;1.5\; &= \;165\; \times \;0.1\; \times 15\; \times \;0.1\\ & = \;165\; \times \;15\; \times \;0.01\\ &= \;(165\; \times \;10)\; + \;(165\; \times \;5 )\; \times \;0.01\\ &= \;(1\;650\; + \;825)\; \times \;0.01\\ &= \;2\;475\; \times \;0.01\\ &= \;24.75\end{align}\)

Division

In the course of their learning, students have learned that a division such as \(12 \div 3\) can be performed according to a context in which groups of three elements are created (sense of grouping or quotative) or according to one in which three equal groups are created (sense of sharing or partitive). These two contexts also exist when a decimal number is divided by a whole number.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 83.

However, in Grade 6, students divide a whole number by a decimal number. During this type of division, the contexts generally call for a division which has the sense of grouping, the question being: "How many tenths are there in this quantity? ".

Source: modified from Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.

Example

A ribbon measuring 110 cm is cut into 5.5 cm pieces to make loops. How many loops can be created?

\(110\; \div \;5.5\; = \;?\)

Estimation

\(\begin{align}110\; \div \;5.5\; &\approx \;100\; \div \;5\\ &\approx \;20\end{align}\)

• Division using multiplication

\(5.5\; \ \times \;?\; = \;110 \)

\(5.5\; \times \;20\; = \;110\)

20 loops can be created.

• Division using an area model

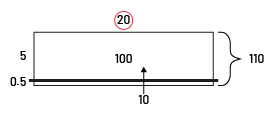
Division of a whole number by a decimal number can be performed using a variety of strategies, strategies that are essentially the same as those used in division situations with whole numbers. However, it is important that students interpret the result correctly. To do this, they must refer to the estimation made beforehand to ensure the order of magnitude of the quotient. They must also refer to the context to ensure that the quotient makes sense, namely, that the result obtained represents the size or number of groups. Students must also understand and be able to explain the strategy used to perform the operation.

Often, when dividing a decimal number represents the grouping sense, the operation is not performed according to that sense since representing a grouping reasoning requires the creation and interpretation of a part of a group, which makes the process more difficult to grasp.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 107-108.

To divide decimal numbers, an equivalent division statement with a whole number divisor can be used since the results will be the same.

Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.

Example

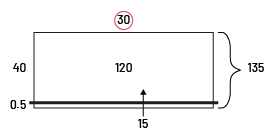
Min is reading a 135 page book. Her goal is to read the book in 4.5 days. How many pages does she need to read per day in order to reach her goal?

Estimation

\(\begin{align}135\; \div \;4.5\; &\approx \;135\; \div \;5 \approx \;(100\; \div \;5)\; + \;(35\; \div \;5)\\ &\approx \;20\; + 7\\ &\approx \;27\end{align}\)

• Division performed using an equivalent division

We need to divide 135 pages by 4.5 days. An equivalent division using natural numbers is 1350 ÷ 45, since I multiply each number by 10 to eliminate the decimal point.

\(\begin{align}135\; \times \;10\; &= \;1350\\4.5\; \times \;10\; &= \;45\end{align}\)

\(1350\; \div \;45\; = \;30\)

Then \(135\; \div \;4.5\; = \;30\)

Min has to read 30 pages a day.

• Division using an area model

The Remainder

In division, the concept of a remainder arises when the quotient is not a whole number. For many students, the remainder is just a number that appears in the "recipe" for division (for example, \(178 \div \;0.8 = \;222\) remainder 4).

However, when the operation arises from a context, the remainder must be processed in order to adequately respond to the problem. Thus, students can develop the ability to process the remainder if they are in a problem-solving situation. Here are several ways to process the remainder:

• the remainder is distributed equally and expressed as a decimal number;
• the remainder is divided equally and expressed as a fraction;
• the remainder is distributed among the groups;
• the remainder increases the quotient by 1;
• the remainder is the answer.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 3, Nombres décimaux et pourcentages, p. 86-87.

Example

In Grade 7, students perform division of a decimal number by a decimal number.

Example

The distance from the provincial capital, Toronto to the national capital, Ottawa, is 450.5 km. A bus driver took 4.75 hours to travel this distance. What is the approximate speed, in kilometres per hour, of the bus?

Estimation

It took about 5 hours to travel about 450 km. How many groups of 5 are there in 450? (\(5\; \times \;?\; = \;450\))

I estimate that the bus travels at an average speed of about 90 (km/h).

• Division performed using an equivalent division

Like multiplication, division with decimal numbers can be calculated like division with whole numbers. It can be performed as if the quotient and the divisor were whole numbers.

\(\begin{align}450.5\; \div \;4.75\; &= \;(450.5\; \times \;100)\; \div \;(4.75\; \div \;100)\\ &= \;45\;050\; \div \;475\end{align}\)

Note: Beginning in the junior grades, students explore and use personal algorithms as well as standard algorithms to find the quotient.

To find the average speed, the distance is divided by the travel time.

• Division performed with the standard algorithm

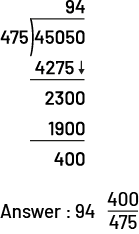
I can therefore say that the approximate speed of the bus is 94 km/h.

Generalization

The reasoning used above allows us to make a generalization about the division of decimal numbers.

For example, \(45.5\; \div \;0.45\) is equivalent to \(455\; \div \;4.5\) and \(4\;550\; \div \;45 \).

Knowledge: Decimal Numbers

---

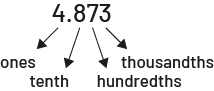
A number that has a decimal point, such as 3.75. The part before the decimal point represents a whole number amount, and the part after the decimal point represents a value that is less than one.

Example

4.873 four and eight hundred seventy-three thousandths

Source: The Ontario Curriculum, Mathematics Curriculum, Grades 1-8, Ontario Ministry of Education, 2020.