Activity 1: Scale Model
This activity integrates concepts in Numbers, Science and Technology, and Art Education.
The teacher explains that a toy manufacturer has given him a sketch of one of their dollhouses. He shows the students the sketch, focusing on its dimensions and the fact that it is made of rectangle-based prisms.
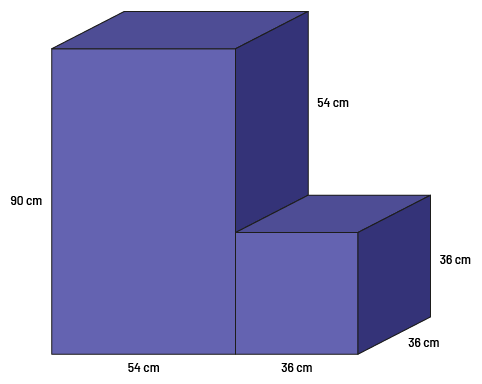
Next, the teacher invites them to create a model of this house that has measurements reduced by half (the ratio of measurements in the model to those in the sketch is 1:2). Depending on the grade, students' proficiencies, and available materials, other ratios may be given to make the model; for example, measurements are reduced to one-fourth (1:4 ratio), two thirds (2:3 ratio) or even doubled (2:1 ratio).
After forming teams of two, teachers provide them with large sheets of cardboard (for example, Bristol board), scissors, rulers, glue, and masking tape or tape, and allow them sufficient time to complete the task (time can also be allowed for decoration, if possible). To complete the task, students can trace the net of the two rectangle-based prisms on large sheets of cardboard. They can then cut them out and build their model.
Once the task is completed, teachers facilitate a class discussion that highlights the various strategies used to build the models.
Note: This activity could be done using other types of plans such as a bridge, tower, simple machine, or landscaping plan.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 108-109.
Activity 2: Proportional or Not? (Identifying Proportional Situations)
Prepare a series of scenarios describing situations that are proportional and others that are not. Divide the students into pairs. Each team will be asked to make a chart as shown below.
| Proportional | Non-Proportional | Justifications | If yes, write the ratio. |
|---|---|---|---|
Afterwards, students must justify the reason for their placement. For proportional situations, they must write the corresponding ratio.
Give feedback as a class. Emphasize the importance of the students' justifications.
Examples of scenarios:
- One bread recipe says to add 1 tablespoon of sugar to every 2 cups of flour.
- A lawnmower mix requires 10 mL of oil for 3 litres of gasoline.
- The basket ball team selects 1 out of 7 people, regardless of the number of candidates.
- Pedro eats a piece of pizza in each of the different pizza sizes.
- A car is driving at a constant speed of 80 km/h.
- For every $5 she earns, Myriam sets aside $1 in her savings account.
- Al invests $2 in a savings account and invests twice as much the next month, then twice as much the next month, and so on.
- The amount he invests compared to the previous month.
- The total amount in his bank account.
Extension
Make a table of values and a graphical representation for all proportional situations.
Activity 3: The Right Choice!!! (Identify the Proportional Relationship)
Divide students into teams of four. Project the following five situations on the board. Individually, the students must choose two situations that are proportional and highlight their arguments to justify their choices. Then, each student in the team, in turn, must convince the other members of their team of their choices.
- Pass half of the questions on an assessment.
- 3 correct answers out of 5 questions.
- 5 out of 7 questions passed.
- 60 percent success rate.
- Out of 40 questions, there were 25 correct answers.
