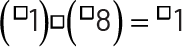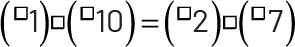B2.4 Use objects, diagrams, and equations to represent, describe, and solve situations involving addition and subtraction of integers.
Activity 1: Let's Talk Integers (Equations to Represent and Describe Situations Related to Addition and Subtraction of Integers)
Write scenarios (see examples below) on cards that students will describe and represent using objects or diagrams.
Organize the classroom desks into islands. Each island represents a workstation. Group students into teams of three. They will rotate through the workstations.
As the activity unfolds, circulate, observe and listen to students' conversations and comments. Note whether they understand and can describe various situations involving negative integers or various ways of representing them.
Review as a class to see if there are any differences in the students' responses.
Extensions
Have each team write a situation that involves negative integers.
Station 1
Write an equation that represents the situation represented by the two colours of counters below and invent a situation that could explain it.
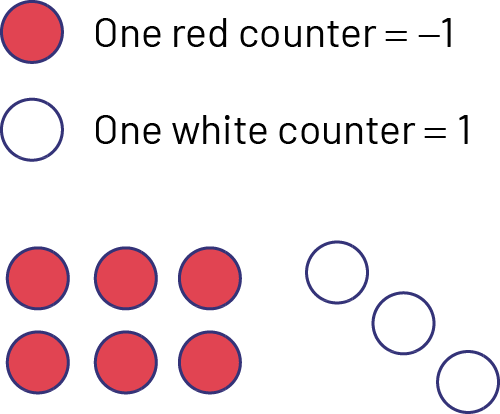
Station 2
Write an equation that represents the situation shown on the number line below and make up a situation that could explain it.
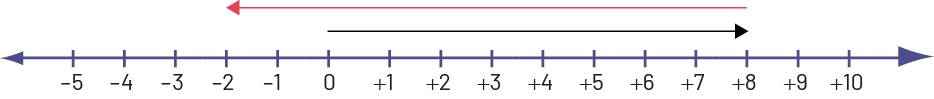
Station 3
The city of Kingston has an average temperature of -6°C in January. Fort Saverne First Nation has an average temperature of -22.5°C.
Write an equation that allows you to find the temperature difference between these two places.
Station 4
In Canadian football, teams attempt to advance down the field in an effort to score a touchdown. On occasion, teams receive penalties and have to go backwards down the field; the ref drops the ball in the right spot for play to start again. Lengths are measured in yards.
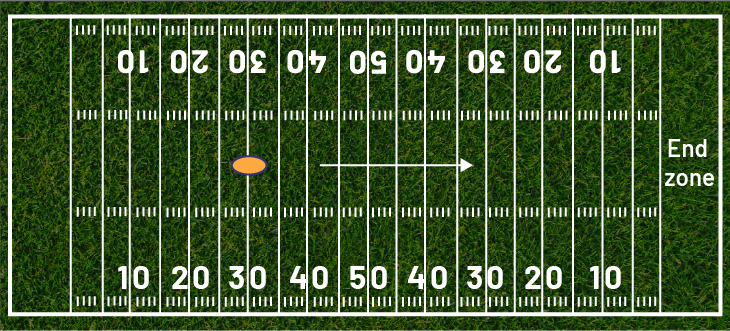
The offensive team wants to get into the end zone shown in the diagram above. The kickoff is taken from the 30 yard line, as shown by the ball in the diagram. On their next play, the offensive team gains 14 yards, but receives a 10 yard penalty.
Write an equation that determines where on the field the ball will be dropped by the referees.
Station 5
For the Grade 7 end-of-year trip, Zachary goes to the water park with his class. He brings $20 to spend. When he gets there, he spends all his money on dinner. He borrows $12 from his friend so he can play in the arcade.
Write an equation that represents this situation and explain its meaning.
Station 6
Altitude is defined as the height above sea level. A diver is on a platform that is 2 metres above sea level. Her mission is to get to a wreck on the sea floor. To reach her goal, from the platform, she jumps into the water. At first, from the surface of the water, she descends 6 m and then another 7 m.
Write an equation that gives the altitude of the diver once she reaches the wreck. Explain its meaning using words and/or drawings.
Other station possibilities: golf score, elevator, the stock market, thermometer, borehole, launching a projectile vertically into the air and falling into the ocean.
Activity 2: The Right Choice (Addition and Subtraction of Integers)
Provide a visual representation of a scenario with three descriptions, one of which is correct. The students must choose the description that correctly describes the situation and then justify their choice.
Prepare the scenarios on paper strips and place them in an envelope. Put 10 strips of the same scenario in each envelope.
Divide students into teams of three and give one envelope per team.
Examples of questions on the paper strips
Paper Strip 1
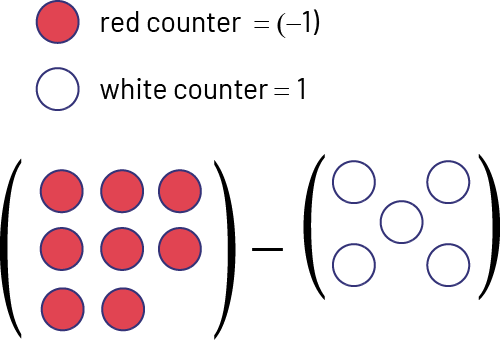
Which of the following statements describes this situation and gives the correct answer? Justify your choice.
- \(( + 8)\; - \;( - 5)\; = \;13\)
- \(( - 8)\; - \;( - 5)\; = \; - 3\)
- \(( - 8)\; - \;( + 5)\; = \; - 13\)
Paper Strip 2

Which of the following statements describes this situation and gives the correct answer? Justify your choice.
- \(( - 6)\; + \;( + 8)\; = \; + 2\)
- \(( - 8)\; - \;( + 6)\; = \; - 14\)
- \(( + 6)\; - \;( + 8)\; = \; - 2\)
Activity 3: Plus or Minus (Addition and Subtraction of Integers)
Formulate equations with missing + and - symbols. The students must complete them so that they are true.
Model a couple of equations to clarify the expectations.
Then, ask each student to formulate five equations. Collect their equations. Divide students into teams of two and give them ten random problems to solve.
Encourage students to use manipulatives (two colours of counters) or the number line to validate.
Observe and record students' comments. Review as a group.
Examples of consolidation questions
- How did you go about completing your equations? How did you choose the symbols?
- Did you use the two colours of counters? Number lines? Why or why not?
- Can an equation have more than one solution?
Examples of equations to complete