General Foundations of Spatial Sense
Primary Division
Because of the connections between the two former strands of Measurement and Geometry and Spatial Sense, the 2020 Mathematics Curriculum integrates these two strands into one, Spatial Sense. Geometry and Measurement are elements of this strand developed in the two expectations, E1 (Geometric and Spatial Reasoning) and E2 (Measurement).
Spatial Sense
Although spatial sense underlies the learning of geometric concepts, it also plays a key role in the development of a sense of measurement. According to Piaget (as cited in Lehrer, 2003), understanding measurement leads to a mental restructuring of space and supports more and more subdivisions of space. These subdivisions are translated into a quantity, or measure.
According to Clements (1999), both children's and adults' spatial sense depends on mental maps that are made up of personal knowledge and include different ideas and processes that can be organized according to various reference schemes and representations which are more spatial than visual. In order to demonstrate spatial sense, students need spatial skills, including spatial orientation and the ability to visualize (visualization). Spatial orientation allows one to locate their position in relation to objects or points in space, and effectively and efficiently move within and around their environment. Students understand and make connections between their different positions in space.

The table below summarizes how these two spatial skills are defined in the context of measurement and geometry.
|
Skill |
Examples |
|
Spatial Orientation Ability to locate oneself or objects in one's immediate physical space, and to make or describe movements in that space. |


|
|
Visualization Ability to form and describe a mental representation of places, objects and movements in two- or three-dimensional space. |
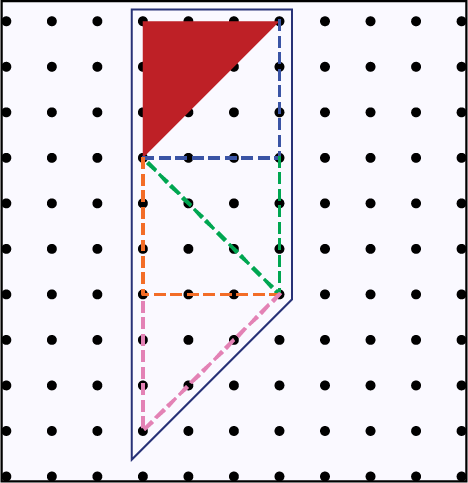 Image On a dotted surface, 5 figures are placed together. 2 triangles form a square, which is stuck to 2 triangles which form a square, and a final triangle. The figures are placed vertically. Image On a dotted surface, 5 figures are placed together. 2 triangles form a square, which is stuck to 2 triangles which form a square, and a final triangle. The figures are placed vertically.
|
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 9-11.
Geometry Fundamentals (Expectation E1)
Geometry Is:
- the study of the figures and objects in physical space;
- the study of relationships between points, lines, curves, surfaces and volumes in space;
- an intuitive knowledge of the shapes and the relationships between them;
- an area of study that enables students to apply complex spatial reasoning to solve problems in all areas of mathematics and in other real-life situations at school, at home, at play;
- a variety of exploration activities with geometric objects.
Geometry is Not:
- an innate knowledge received at birth by a few rare individuals;
- teaching or learning that focuses solely on rules, procedures, analytical reasoning and demonstrations;
- memorization of definitions and theorems;
- solely the study of shapes and three-dimensional objects.
Levels of Geometric Thinking
Over the past several years, studies in the field of geometry have had an important influence on the teaching of geometric concepts. As a result of extensive research, two Dutch researchers, Dina Van Hiele-Geldof and Pierre Van Hiele, have developed a model of the development of geometric thinking. The key element of this model is a five-level hierarchy describing the understanding of geometric concepts at different stages of a student's thinking development.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 2-3.
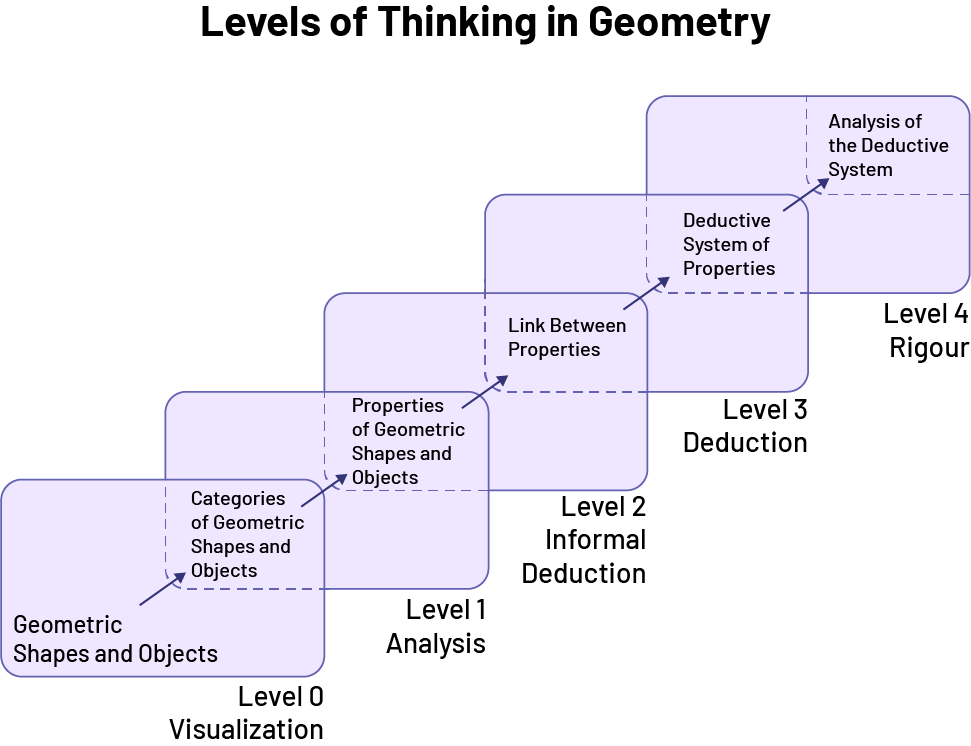 Image Categories of geometric shapes. Level zero: visualization. Level one: analysis. Level 2: informal deduction. Level 3: deduction. Level 4: rigour. Each level is accompanied by a note card. Starting from level zero, geometric shapes, categories of geometric shapes, one, properties of geometric shapes, 2, link between geometric shapes, 3, deductive system of properties, 4, analysis of the deductive system.
Image Categories of geometric shapes. Level zero: visualization. Level one: analysis. Level 2: informal deduction. Level 3: deduction. Level 4: rigour. Each level is accompanied by a note card. Starting from level zero, geometric shapes, categories of geometric shapes, one, properties of geometric shapes, 2, link between geometric shapes, 3, deductive system of properties, 4, analysis of the deductive system.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 12.
A brief description of these five levels, as well as the observable behaviours for each, is presented in the following table.
|
Description |
Observable Behaviours |
|
Level 0 - Visualization |
Level 0 - Visualization |
|
Perception of two-dimensional shapes and three-dimensional objects based on their appearance rather than their properties. |
The student:
Sample statement: ✓ It's a square because it looks like a square, because I see it, because it's square. |
|
Level 1 - Analysis |
Level 1 - Analysis |
|
Beginning of the analysis of two-dimensional shapes and three-dimensional objects to discover their properties. |
The student:
Sample statement: ✓ This figure is a square because it has four vertices. ✓ This figure is a square because it has four right corners. ✓ This figure is a square because it has four equal sides. ✓ This figure is a square because it has two pairs of parallel sides. |
|
Level 2 – Informal Deduction |
Level 2 – Informal Deduction |
|
Establishment of connections or relationships between properties of a two-dimensional shape or a three-dimensional object and between shapes or objects. |
The student:
Sample statement: ✓ It is a square, but it is also a trapezoid, because the property that describes the trapezoid is that at least two opposite sides are parallel. So I believe that the square is a kind of trapezoid. ✓ A square is a rectangle, parallelogram, and quadrilateral because it has all the properties of these three polygons. A cube is also a square-based prism or a rectangular-based prism. |
|
Level 3 - Deduction |
Level 3 - Deduction |
|
Study of definitions, proofs of theorems, axioms and postulates. |
The student:
Sample statement: ✓ A parallelogram that has two adjacent sides of equal length must be a rhombus. |
|
Level 4 - Rigour |
Level 4 - Rigour |
|
Study of geometry in an abstract way. Note: Little research has been done on this level. |
The student:
|
The student is not necessarily at a particular level depending on age or grade. In grades 1 to 5, depending on the concepts presented, they are generally at the visualization or analysis level.
For example, the student describes some properties of the square (analysis level), but recognizes the parallelogram only by its appearance (visualization level).
In order for the student to move from one level to the next, they must have a variety of geometry experiences that must be accompanied by effective instructional interventions by teachers.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 3-5.
Overview of the Big Ideas in Geometry
The following Big Ideas are presented, explored, and developed to support teachers in planning their instructional strategies and assessments. While interrelated, each Big Idea has a particular emphasis.
Big Idea 1: Geometric Relationships
Connections can be made between geometry and spatial sense and the world around us.
Big Idea 2: Geometric Properties of Two-Dimensional Shapes and Three-Dimensional Objects
Two-dimensional shapes and three-dimensional objects, and their properties, allow us to describe the world around us.
Big Idea 3: Location and Movement
The position and placement of two-dimensional shapes and three-dimensional objects allow us to situate them in the world around us.
The Big Idea of Geometric Relationships connects the other two Big Ideas, since learning geometry and spatial awareness requires students to make connections with the world around them.
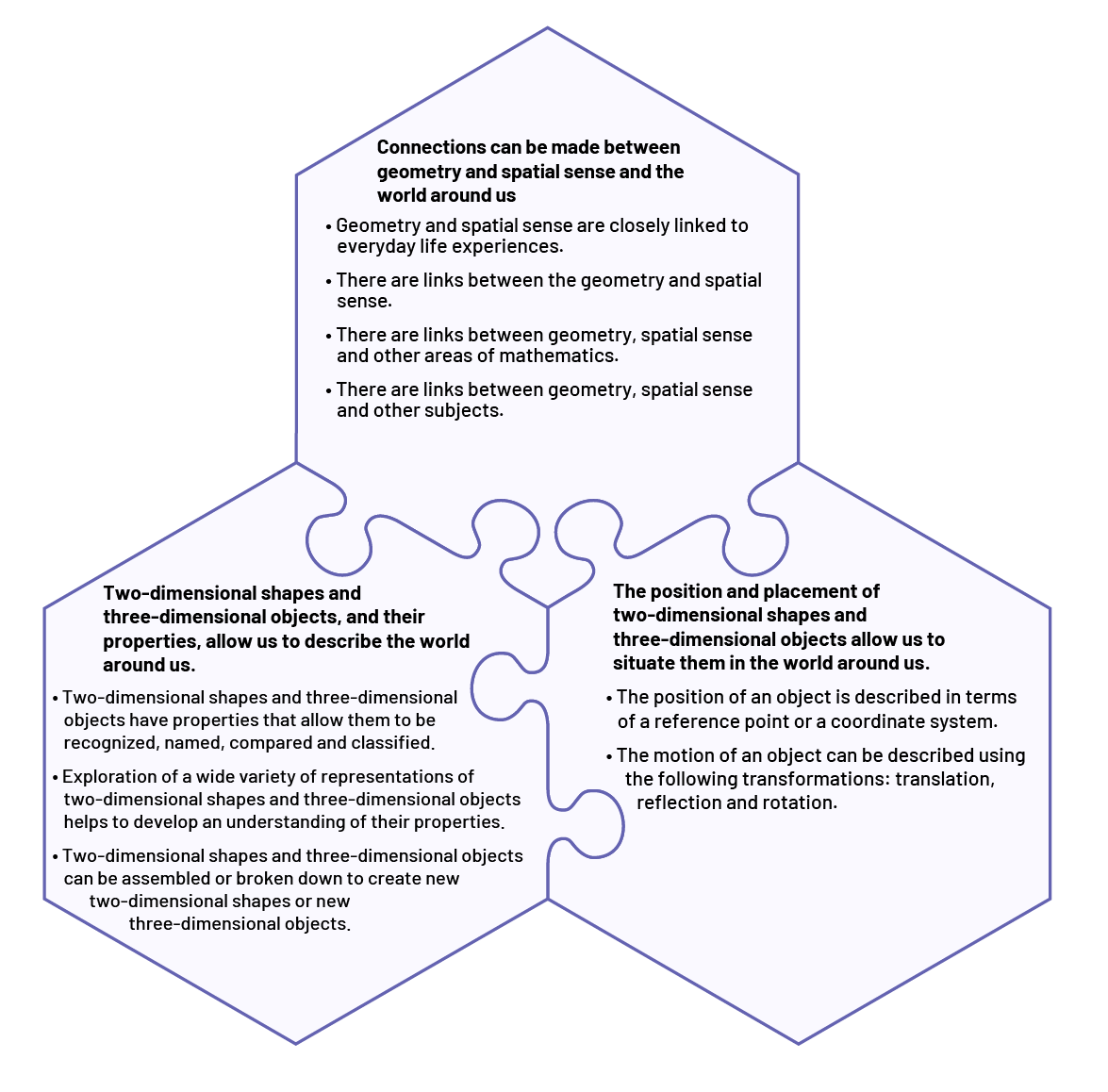
Source: translated from Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 9-10.
Measurement Fundamentals (Expectation E2)
Measurements enable us to mark out our activities. They guide our thoughts, our decisions, and our perceptions of the world. Measurements are so deeply ingrained in our daily activities that we often overlook their presence and importance. We regularly ask ourselves questions such as 'Who has more than me?', 'How far is this?', 'How high or long is this object?', without necessarily thinking that we are using a measurement. In any situation, it is possible to measure different characteristics of an object. It is therefore important to specify the characteristic, commonly called an attribute, that is being measured.
The following are examples of measurable attributes that can be quantified by various non-standard and standard units of measurement.
|
visual acuity |
sound intensity |
size |
|
area |
length |
temperature |
|
angle |
mass |
time |
|
capacity |
perimeter |
speed |
|
chill factor |
population |
volume |
|
frequency |
depth |
|
|
UV index |
acreage |
Attribute: A characteristic related to the physical appearance of an object, person, or occurrence, identified on the basis of observation or through manipulation.
Measurement is complex and involves skills that go beyond the ability to measure with a measuring instrument or tool such as a ruler or a clock. Students should be able to recognize, compare, measure and estimate with ease the measurable attributes of an object, in various contexts. Through a variety of learning experiences focused on solving everyday problems, students should come to recognize how these concepts are used in everyday life.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 5-7.
Measurement
For some students, measurement skills may appear to be innate, as if they are inherited at birth. However, research shows that students can develop measurement skills through activities that incorporate the manipulation of concrete materials and the use of non-standard and standard units of measurement. The development of measurement skills goes beyond learning skills and procedures related to the act of measuring. It is a structured and organized path that evolves and must be adapted to the various measurable attributes of an object.
Buys and de Moor (2005) point out that the primary goal of measurement instruction is to develop a sense of measurement, and that to achieve this goal, teachers must bring students to:
- recognize everyday situations that call for measurement;
- develop the ability to distinguish the different measurable attributes of an object and determine the situations in which to apply them;
- visualize the various units of measurement related to the different attributes;
- use measurement vocabulary correctly.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 8.
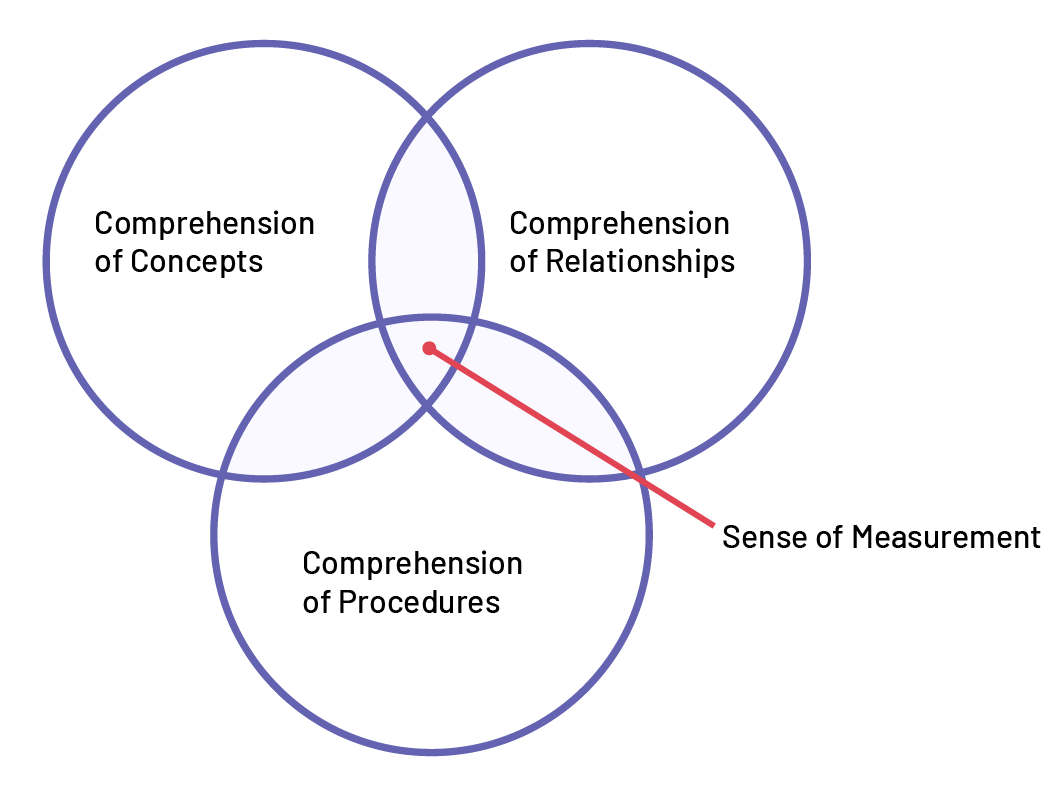 Image Venn diagram made up of three circles. The shared section of the three circles is the sens of the measure. Circle one: comprehension of the concepts. Circle 2: comprehension of the relations. Circle 3: comprehension of the procedures.
Image Venn diagram made up of three circles. The shared section of the three circles is the sens of the measure. Circle one: comprehension of the concepts. Circle 2: comprehension of the relations. Circle 3: comprehension of the procedures.The meaning of measurement is to build concepts related to measurement, establish relationships in measurement and know how to apply procedures to determine the measurement of an object.
Overview of Measurement
The learning content of Expectation E2 (Measurement) involves a large number of concepts. To help teachers plan and implement strategies that provide effective and coherent instruction, these key concepts are grouped under one Big Idea, Measurement Sense, including: fundamental attributes and concepts, measurement relationships, and the act of measuring.
Big Idea - Measurement Sense
The exploration of various attributes, relationships, and procedures related to the act of measuring develops a sense of measurement.
Key Concept 1 - Fundamental Attributes and Concepts
Understanding the attributes that can be measured and the fundamental concepts behind them gives meaning to the units of measurement and the act of measuring.
Key Concept 2 - Measurement Relationships
Understanding measurement relationships facilitates the ability to formulate conjectures and generalizations.
Key Concept 3 - Measurement Tools and Procedures
Understanding the procedures requires taking ownership of all the steps in the act of measuring in order to consolidate the concepts of measurement.
In the primary grades, students develop their sense of measurement by exploring the attributes of length, area, capacity, mass, and time. They use comparison, juxtaposition of units of measurement, and some instruments to determine the measurement of these attributes using non-standard units of measurement and standard units of measurement for length and time. Students primarily explore the inverse relationship and some relationships between the standard units of measurement under study.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 41-42.
Ability to Visualize
The ability to visualize involves forming a mental image of a situation or an abstract concept. In measurement, this ability is mainly related to the ability to form a mental image of:
- certain measurable attributes;
- benchmarks associated with the various attributes.
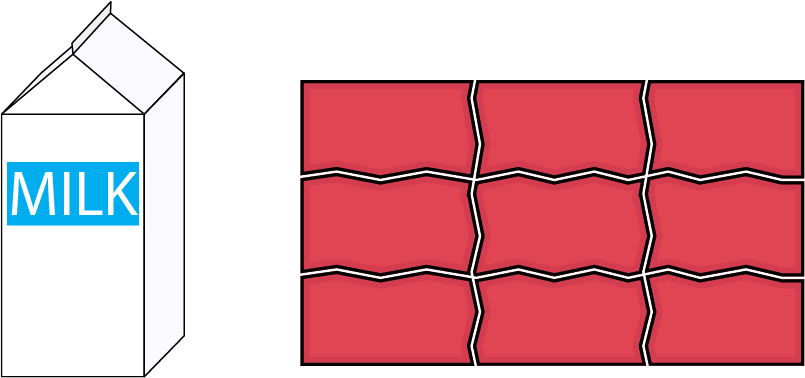
Visualizing certain measurable attributes: the ability to visualize certain measurable attributes supports conceptual understanding of those attributes. In the primary grades, students explore the attributes of length, area, and capacity, time and mass. For the attributes of time and mass, since they do not represent something that can be seen or illustrated, students can at best form a mental image of a few appropriate benchmarks.
For length, students will need to visualize a straight line or curve in a one-dimensional space. For example, when they are asked to determine the perimeter of a given shape, they might visualize that they are placing a string around that shape and determining the measure of each of the sides.
Students should also recognize that in some situations, length might be named in another way, for example:
- the height of a mountain;
- the width of a prism;
- the thickness of a cake;
- the height of a person;
- the depth of a lake;
- the perimeter of a box.
For area, students will need to visualize a flat or curved surface in a two-dimensional space. For example, when they are asked to determine the area of a given rectangle, they must visualize that they are determining the measure of the space occupied by the surface of this shape.
Additionally, students should recognize that in certain contexts, area might be referred to differently. For example:
- the acreage of a piece of land;
- the land area of a city.
For capacity, students will need to visualize a three-dimensional object. For example, in a situation when they are asked to determine the capacity of a container, they should visualize how much that container can hold.

Visualize benchmarks: the ability to form mental image benchmarks associated with measurable attributes helps students estimate the measure of an attribute or check the reasonableness of a result obtained from using a measuring tool or applying a formula. For example, consider a student who selects the chalkboard ruler (which represents 1 metre) as a benchmark. They can create a mental image of this ruler and use it to estimate that the length of a classroom wall is about 4 metres.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 20-22.
In geometry, students in the primary grades investigate the properties of two-dimensional shapes and three-dimensional objects through construction activities (for example, building with a geoboard, straws, playdough, cardboard, interlocking cubes) and drawings on paper (for example, representation on graph paper, dot paper).
These activities help students construct a mental representation of two-dimensional shapes and three-dimensional objects based on specific properties and promote the development of visualization skills.
The manipulative activities with concrete materials and construction with the geoboard are particularly useful for this purpose.
To help students develop the ability to move from one space to another and to consolidate their knowledge of the properties of three-dimensional objects, teachers can use a variety of construction activities (for example, building a model with cubes, building the shell of a solid from a given net) and a variety of representation activities (for example, tracing the net of an object, matching an object to its net).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 28-29.
Spatial visualization can be developed by attending to the following spatial skills.
|
Spatial Skills Related to Spatial Visualization |
Description |
|
1. Oculomotor coordination |
Ability to coordinate vision and body movements. |
|
2. Perception of plans (form and content) |
Ability to perceive a specific element on a complex background (intersections, superimpositions). |
|
3. Constancy of forms |
Ability to recognize geometric shapes and objects regardless of their size, color and orientation in space. |
|
4. Perception of positions |
Ability to perceive the position of an object in relation to oneself. Ability to discriminate between identical objects, regardless of their orientation. |
|
5. Perception of spatial relationships |
Ability to perceive the position of two or more objects in relation to oneself or one object in relation to the other. |
|
6. Visual discrimination |
Ability to notice similarities and differences between two or more objects. |
|
7. Mental rotation |
Skill in '[…] mentally rotating two-dimensional shapes or three-dimensional objects' (Ontario Ministry of Education, 2014, p. 13). |
(John Del Grande, 1990. © 2019, National Council of Teachers of Mathematics. The Arithmetic Teacher, vol. 37, no. 6.)
Source: translated from Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, Mesure et géométrie, Fascicule 3, p. 12-13.
Ability to Solve a Problem Situation
Solving problems is essential to learning measurement. To help students develop this skill, teachers should present various types of problem situations with meaningful contexts. Teachers should encourage students to use their measurement knowledge, and problem-solving strategies, to clearly communicate their results, and to discuss their ideas during mathematical exchanges.
Measurement problems should contribute to students' understanding of fundamental attributes and concepts, measurement relationships, and appropriate tools and procedures for measuring attributes.
Example
Students must determine which of two trails on a bike trail map is longer. Both trails start at the same point on the map, at the entrance to the park, and one ends a little further into the park than the other. They are given a piece of string that has been pre-measured to be longer than the route of the longer trail. Students must justify their results with mathematical arguments and explain the methods used to make the comparison.
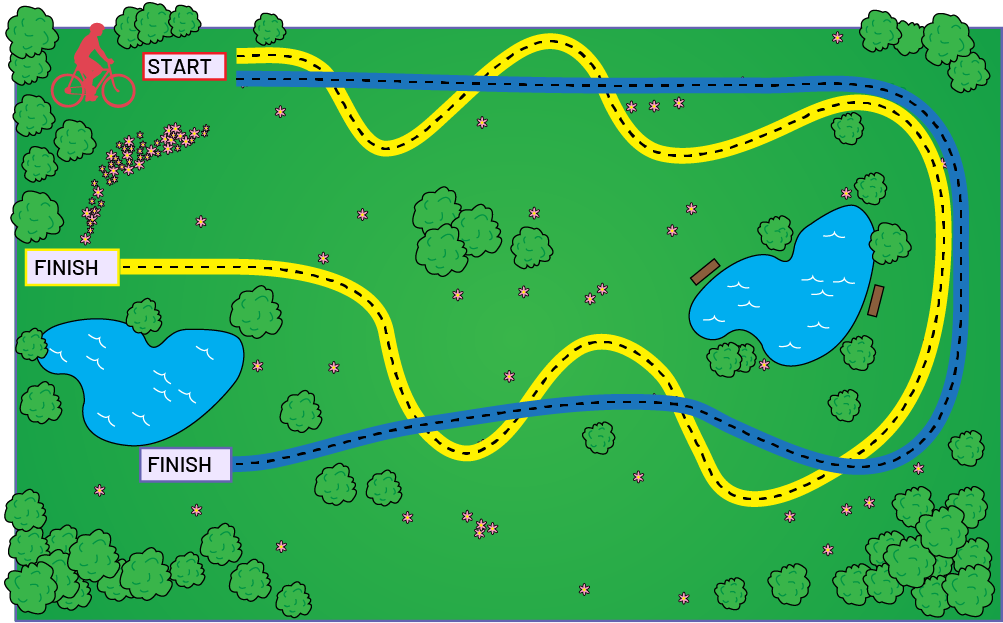 Image a card with two possible trajectories, for a bike. One of the trajectories is in blue, the other is in yellow. The two trajectories have a common starting point, but a different point of arrival.
Image a card with two possible trajectories, for a bike. One of the trajectories is in blue, the other is in yellow. The two trajectories have a common starting point, but a different point of arrival.
During a mathematical exchange, the teacher invites students to justify their answer by asking questions such as:
- Which is the longest trail? How do you know? (I looked at where each trail started and ended. I saw that the end point of the yellow trail was farther than the end point of the blue trail)
- Does the fact that the end point of the yellow trail is further away than the end point of the blue trail mean that the yellow trail is longer than the blue trail? Justify your answer.
- Are there other ways to determine which trail is longer? (I measured each trail with a piece of string. The string on the yellow trail was longer than the string on the blue trail. I could have used playdough, pipe cleaners, or small interlocking cubes.)
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 22-23.
Reasoning Skills
Reasoning is a mental process in which ideas are logically connected. It is an important skill because it allows students to structure their thinking by integrating knowledge and establishing relationships between ideas and concepts. In measurement, there are many relationships to be understood (for example, relationships among attributes, relationships among units of measurement). Reasoning in a measurement context involves analyzing the similarities and differences among measurable attributes, to drawing conclusions, and, ultimately, to applying knowledge in a new context. By asking students to justify their reasoning and explain their approaches to solving problems, teachers can foster intellectual curiosity and lead students to move beyond a simple answer to reflect on the fundamental concepts of the attributes.
To help students develop the ability to reason in measurement situations, teachers should ask open-ended questions and provide varied and complex problem situations. They should encourage students to:
- concretely represent their thinking;
- explain their process and justify their results;
- observe and analyze the strategies used by other students.

The cardboard is 14 small paperclips long. If I measure the cardboard with large paperclips, I will need fewer paperclips.
Note: Teachers sometimes tend to ask students to justify their answers only when they are wrong. As a result, when asked to justify an outcome, students tend to think they have made a mistake. It is therefore important to regularly encourage students to justify their answers, whether they are correct or not. In this way, they will understand that this is simply a step that is inherent in all reasoning.
Questions from teachers and suggestions from peers during mathematical exchanges can help students to:
- realize that it is possible to solve the given situational problem in a simpler way;
- formulate their reasoning;
- make more complex conjectures and generalizations.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 24-25.
The nature of students' mathematical reasoning is closely related to their ability to abstract. At Levels 0 and 1 in the Geometric Thinking continuum, students use mostly inductive mathematical reasoning, going from the particular to the general. For example, when they manipulate a limited number of similar geometric shapes and objects and observe the attributes or properties of these shapes and objects, students begin to associate these characteristics to the set of geometric shapes or objects that are part of the same family. After manipulating a small number of pyramid-shaped objects, for instance, students may conclude that all pyramids have a pointed end.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 36.
Communication Skills
To communicate is to express one's thoughts or feelings in order to be understood. For communication to occur, there must be an intention, a situation, a context, a code, a message and an explicit or implicit interaction between people.
The skill of communicating in measurement is best developed in the context of problem solving or mathematical discussion. In any situation that involves reasoning and mathematical argument, the skill of communicating allows students to develop their understanding of concepts. The social dimension of communication plays an important role in the development of this skill and benefits everyone involved in the act of measuring.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 26.
The ability of students to present a mathematical argument reflects their level of thinking. According to Radford and Demers (2004), students in the Primary Division typically begin constructing mathematical arguments using causal terms such as ‘then’ or because’. However, since they have not always fully understood the notion of causality, they sometimes use these terms incorrectly to justify a conclusion or the solution to a problem (for example, 'It's a square because it looks like a square.'). Teachers can help students develop the ability to use causal terms by giving them the opportunity to respond critically to arguments presented by other students (for example, 'Matéo says it's a square because it looks like a square. Do you think that's a clear and convincing argument?').
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 37.
In the primary grades, oral communication is a prerequisite for written communication.
Oral Communication
Oral communication is the most natural form of expression used by students. Speech remains the most useful and most frequent means of communicating on a daily basis. It is essential to the transmission of ideas, discoveries, approaches, and results in measurement. It serves as a springboard for student reflection and engages them in a structured dialogue that helps them give meaning to their explorations. To help students develop this skill, they need to be provided with various opportunities to express themselves and demonstrate their understanding of different concepts.
In the primary grades, during team learning situations and mathematical exchanges, students need to learn to use vocabulary related to attributes and non-standard units of measurement, to compare objects with each other using appropriate terminology, and to describe measurement using correct and accurate terms.
For example, when comparing their stuffed animals, children can say:
- My bear is longer than yours;
- Mine is shorter than yours;
- Zoe's is the same height as Dylan's.
When students are introduced to standard measurement, they must not only compare objects to other objects, but also determine the measurement in correct and accurate terms. For example, they will say, 'The perimeter of the sandbox is 12 metres and the perimeter of the playground is 24 metres.'
For example, if a student says, 'My piece of cake is bigger than yours,' the teacher should prompt the student to clarify by asking if their piece of cake is longer, thicker, or wider than the friend's.
In order to promote communication among students, teachers should reduce the length and frequency of their interventions and allow time for discussion and analysis of ideas from teams or individuals. Before soliciting a response to a question, teachers should encourage group discussion and allow sufficient time for reflection.
Together with the spoken word, the actions taken by the students can contribute to communication by showing the strategy used to solve a problem or to understand a concept in measurement.
Example 1
Students demonstrate their understanding of area by covering the surface with pattern blocks.

I used four blue rhombuses, four green triangles and a yellow hexagon to cover the kite. The shapes do not overlap.
Example 2
The student explains how she used her shoe and finger to measure her friend's height by iteration.
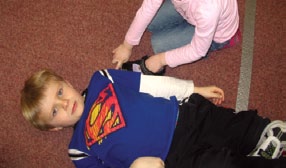
I placed my shoe next to my friend, placed my finger on the end of my shoe and then moved the shoe along my friend to where my finger was to continue measuring.
Written communication is an excellent way for students to clarify their ideas and describe their problem-solving strategies. It is also a good indication of what they have learned. Students often reveal a great deal of what they have learned and mastered through the evidence left on their worksheets. The teacher should encourage them to leave as much evidence as possible.
Example 1
In the early stages of learning, students often formulate their mathematical thinking through drawings and words.

Written communication should encourage the representation of the tools used to solve the problems (for example, a rectangular layout, scales, tape measure). When possible, students should be allowed to use the interactive whiteboard to represent their solution. The interactive whiteboard often allows for a more accurate representation and more complete record.
To help students improve their written solutions, teachers should encourage them to discuss the task and possible solutions, and to use concrete materials and familiar symbols to show their thinking. There are several tools that support the improvement of written communication, such as word walls, graphic organizers, math journal, and interactive whiteboards.

 Image A wall of words for mathematic vocabulary. Measuring lengths: short, shorter, long, longer, meter, centimeter. Measuring time: day, week, hour, minute, year, month, day, season. Measuring weight: heaving, light, heavier, lighter.
Image A wall of words for mathematic vocabulary. Measuring lengths: short, shorter, long, longer, meter, centimeter. Measuring time: day, week, hour, minute, year, month, day, season. Measuring weight: heaving, light, heavier, lighter.In summary, written communication allows students to:
- record their learning and the evolution of their mathematical thinking in a portfolio or mathematical journal;
- take the time to think and organize;
- objectify certain concepts;
- enjoy a space for personal expression.
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 26-31.
Teachers support the development of spatial sense in the classroom. Their role is not only to select tasks, but also to encourage students to go beyond the application of procedures so that they can develop a good conceptual understanding of measurement attributes, geometric properties and other concepts related to measurement and geometry. Teachers should encourage students to make connections between spatial sense concepts, relationships and procedures.
To do this, teachers must:
- select effective teaching and learning strategies;
- strategically select the focus of inquiry;
- plan and structure mathematical exchanges;
- create a learning environment that is conducive to the development of spatial sense.
Choosing effective teaching and learning strategies: a teaching strategy is defined as a way of doing things, an approach, a series of actions and means that teachers use in a given context. Effective teaching in spatial sense leads students to:
- think about attributes and relationships;
- solve measurement problems in both real-life and purely mathematical contexts;
- demonstrate motivation and commitment to solving these problems;
- discuss their trials, possible solutions, and their understanding of concepts and procedures.
Strategically choose focus of inquiry: in order to help students develop mathematical thinking that reflects a spatial sense, teachers must ensure that the questions they ask are appropriate to the time, situation, and level of understanding. Questions should support students to deepen their conceptual understandings, make connections, propose conjectures, and make generalizations.
Planning and structuring the mathematical exchange: Throughout a learning situation, the teacher should plan for the consolidation of learning (the mathematical exchange). To do this, they carefully observe the students' work and determine, based on one or more objectives, which solutions should be presented to the whole class. This work should be chosen to stimulate discussion and help students consolidate their understanding of the targeted skills and concepts.
 Image Students are sitting, in a circle, on the ground, they have large sheets of paper before them. The teacher is with them. She looks at the work of the presenting student.
Image Students are sitting, in a circle, on the ground, they have large sheets of paper before them. The teacher is with them. She looks at the work of the presenting student.
The strategy in which student work is selected and displayed in the classroom based on specific goals is sometimes referred to as the Bansho strategy.
Student work should be selected and displayed to highlight:
- problem-solving strategies used by students (for example, illustrate the variety of strategies used or illustrate the same strategy presented in different levels of structure and organization);
- the materials used by students (for example, illustrate the difference between a representation made with drawings and one made with a ruler, rectangular layout, or symbols);
- the clarity of the proposed solution (for example, illustrate the difference between a partial representation of a solution and one in which students have organized, shown, and explained their solution clearly using words and symbols).
During a mathematical exchange, teachers may also choose to display several pieces of work that have effective but different traces so that students can be exposed to other possible solutions and ways of thinking about the problem. During the mathematical exchange, teachers should structure the conversation by asking leading questions and facilitating sharing as needed. They should ensure that the concepts being discussed are clear and understood by the students and if necessary, model an effective approach, strategy, or procedure to conclude the learning experience. This modelling may be done either by the teacher or by a team of students. A well-structured mathematical exchange allows students to strengthen their knowledge and understanding of concepts and procedures, and to recognize the importance of communicating them effectively.
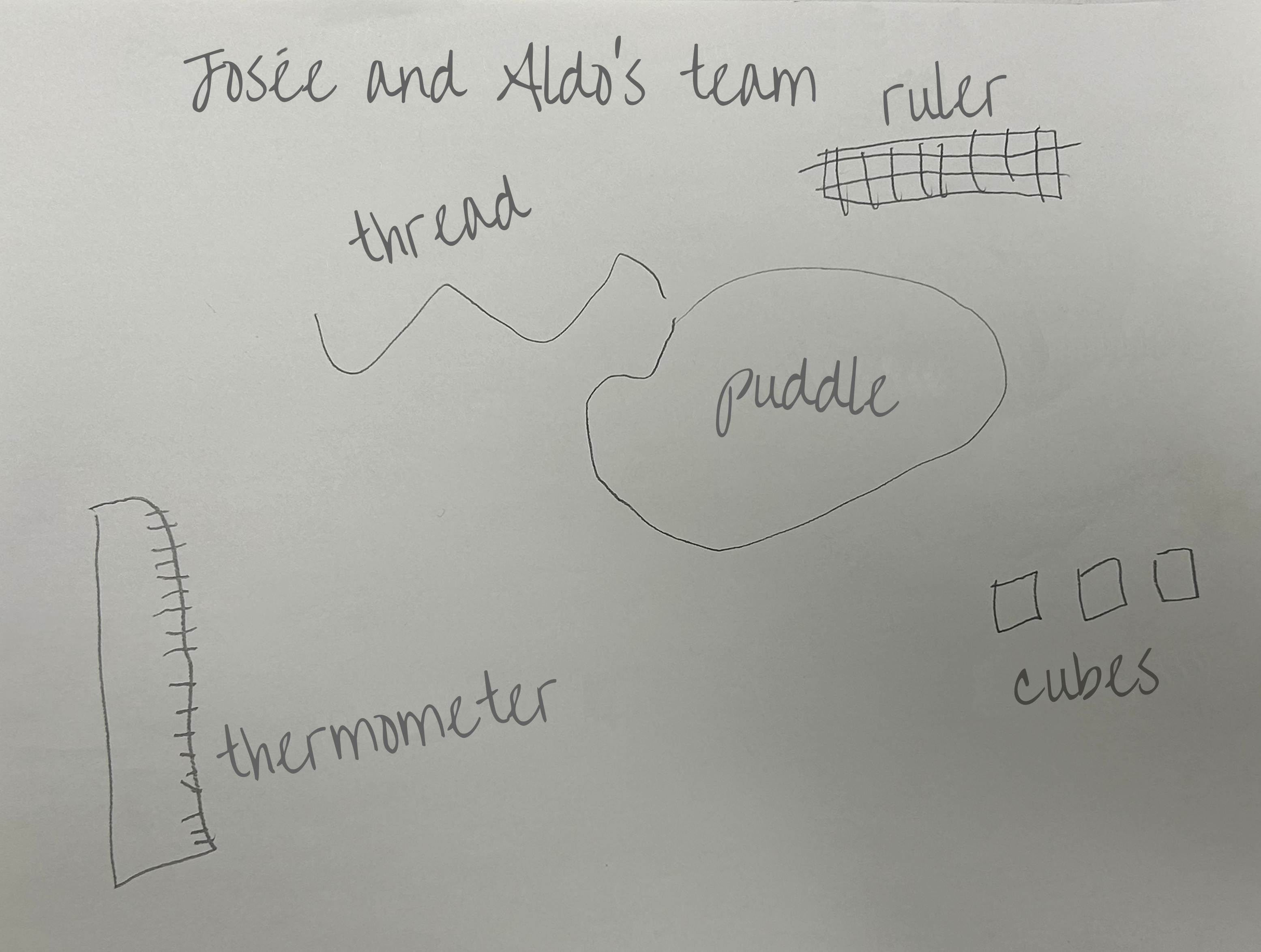
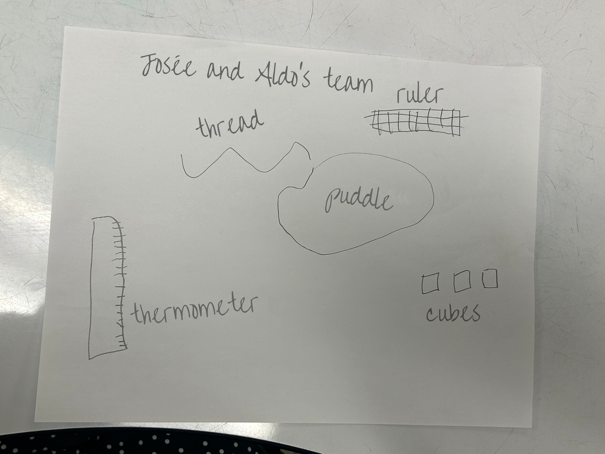 Image An example of student work where the latter have put on paper a representation of their approach. The name of the team, the material used, a thermometer, cubes, a water puddle, thread, a ruler.
Image An example of student work where the latter have put on paper a representation of their approach. The name of the team, the material used, a thermometer, cubes, a water puddle, thread, a ruler. Image Reproduction of student’s work where they put on paper a representation of their approach. The name of the team, the material used, a thermometer, cubes, a water puddle, thread, a ruler.
Image Reproduction of student’s work where they put on paper a representation of their approach. The name of the team, the material used, a thermometer, cubes, a water puddle, thread, a ruler.Note: The order of the presentations chosen allows for two different strategies of representations to be shown to elicit student reflection and discussion. It can be seen that the strategies on the right-hand representation are more detailed and precise than the one on the left. The explanations given make it possible to observe the progression of understanding of the concept.
Creating a learning environment conducive to the development of spatial sense: A learning environment conducive to developing spatial sense is one that focuses on the development of the conceptual understanding of geometric properties, attributes, and units of measurement as much as proficiency with procedures. Teachers must consciously use, both in mathematics and in other subjects, various situations that call on measurement and geometry. It is by being regularly confronted with the need to measure and use geometric reasoning that students understand the importance of developing their spatial sense.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Mesure, p. 37-40.
