At a Glance...

Because of the inextricable links between the two former strands of Measurement and Geometry and Sense of Space, the 2020 Mathematics Curriculum integrates these two strands into one, Spatial Sense. Geometry and Measurement are elements of this strand developed in the two expectations, E1 (Geometric and Spatial Reasoning) and E2 (Measurement).

Spatial Sense

Although a spatial sense underlies the learning of geometric concepts, it also plays a key role in the development of a sense of measurement. According to Piaget (as cited in Lehrer, 2003), the understanding of measurement leads to a mental restructuring of space and thus encompasses more and more subdivisions of space. These subdivisions are translated into a quantity or a measure. 

According to Clements (1999), both children's and adults' spatial sense depends on mental maps that are nothing like a paper or electronic map. They are made up of personal knowledge or characteristics and include different ideas and processes that can be organized according to various reference schemes. The younger the child, the vaguer the connections between the representations. These representations are more spatial than visual. In order to demonstrate a spatial sense, students need to have spatial skills, including spatial orientation and visualization. With spatial orientation, they can locate their position in relation to objects or points in space and move around in their environment. Students understand and make connections between their different positions in space.

The table below summarizes how these two spatial skills are defined in the context of measurement and geometry.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Mesure, p. 9-11.

Geometry Fundamentals (Expectation E1)

Geometric and spatial awareness in the junior grades means developing:

• an understanding of geometric shapes and objects, their properties and the interrelationships between them;
• an intuitive awareness of the position and movement of objects in space;
• informal deductive reasoning and complex spatial reasoning that enable students to solve problems in all areas of mathematics and in a variety of real-life situations at school, at home, or at play.

Geometry and spatial awareness in the junior grades is not:

• an innate knowledge received at birth by a few rare individuals;
• teaching or learning that focuses solely on rules, procedures, analytical reasoning and demonstrations;
• memorization of definitions and properties;
• only the classification of two-dimensional shapes and three-dimensional objects.

Geometry and spatial sense are inseparable since geometry helps us to describe, represent and mathematize spatial reality and spatial sense allows us to visualize, recognize or appreciate this reality.

Levels of Geometric Thinking

---

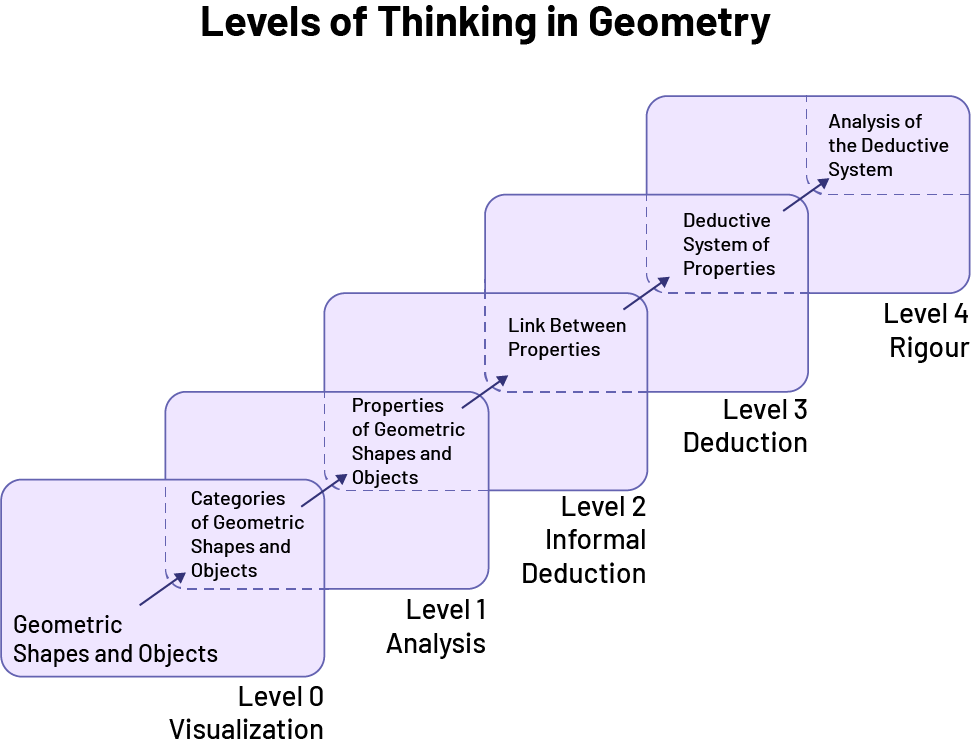Image Categories of geometric shapes. Level zero: visualization. Level one: analysis. Level 2: informal deduction. Level 3: deduction. Level 4: rigor. Each level is accompanied by a note card. Starting from level zero, geometric shapes, categories of geometric shapes, one, properties of geometric shapes, 2, link between geometric shapes, 3, deductive system of properties, 4, analysis of the deductive system.

Two Dutch researchers, Dina Van Hiele-Geldof and Pierre Van Hiele, have devised a five-level model to describe the understanding of geometric concepts at different stages of a student's thinking development. Students can progress from one level of thought to another when they do activities aimed at comparing and classifying geometric shapes and objects and analyzing their properties. Teachers who recognize students' levels of thinking, based on certain observable behaviours, are better able to support students in performing geometric analyses and gradually developing their ability to reason.

A brief description of these five levels, as well as examples of observable behaviours for each, are presented in the following table.

According to the theory, students must go through each of the levels for each new concept. They can therefore be at level 1 (analysis) for one concept and at level 0 (visualization) for another. For example, a student may be able to describe some properties of the square (level 1), but only be able to recognize the parallelogram by its appearance (level 0). Students can progress from one level to another as they engage in activities that focus on comparing and classifying geometric shapes and objects and analyzing their properties. Teachers who know how to recognize students' level of thinking in relation to a given concept based on certain observable behaviors are better able to help them understand this concept and lead them to a higher level of thinking. In general, most students in the primary cycle are mainly at the levels of visualization and analysis.

Teachers in the junior grades should support students to progress to the informal deduction level (Level 2), which will continue into grades 7 and 8.

Note: It is important to remember that the five levels of geometric thinking are not related in any way to the four levels of achievement found in the Mathematics Curriculum Framework Performance Rubric.

Overview of the Big Ideas in Geometry

The Mathematics Curriculum expectations and learning content include a large number of concepts. Big Ideas help teachers see how these concepts can be grouped together to allow for more effective instructional programming. By planning instruction around Big Ideas and their associated concepts and skills, teachers are able to develop coherent learning situations that allow students to:

• explore concepts in depth;
• establish links between the different concepts;
• recognize that mathematics is a coherent whole and not a collection of isolated pieces of knowledge.

In the following section, we discuss two Big Ideas in geometry and spatial sense, each supported by two concepts that underlie it.

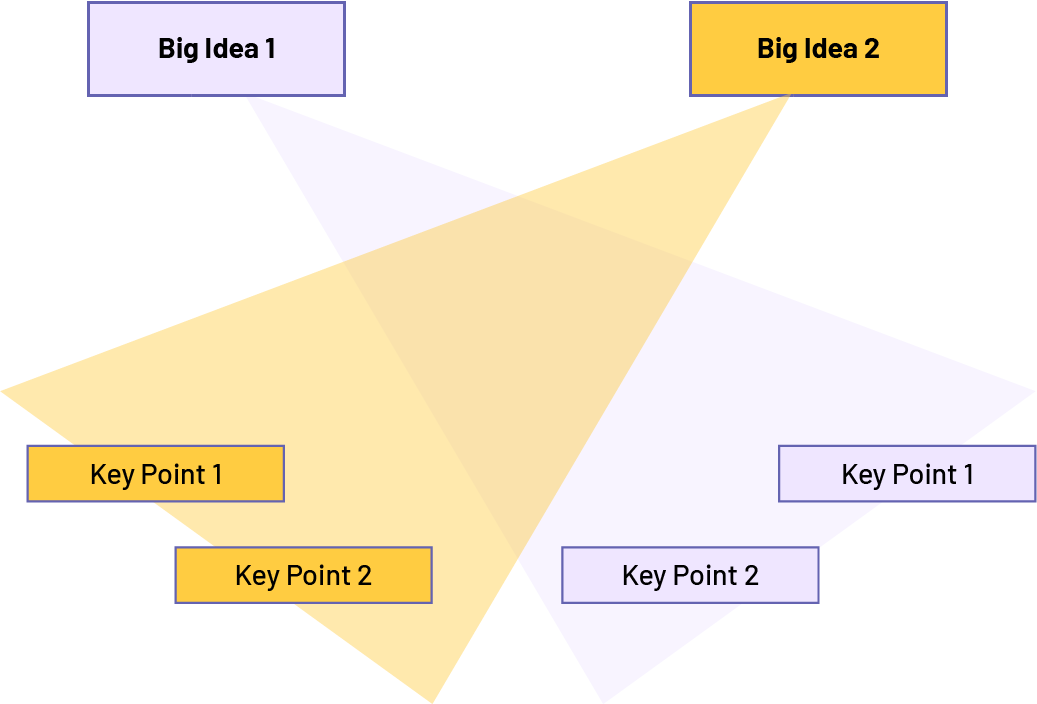
The two Big Ideas that form the basis of Expectation E1 (Geometric Reasoning) in the Spatial Sense strand in Grades 4-6 are:

Big Idea 1: Geometric Reasoning

The knowledge of geometric shapes and objects and their properties allows us to mathematize the world around us.

Big Idea 2: Location and Movement

The concepts of location and movement in geometry help develop a sense of two- and three-dimensional space.

The two Big Ideas overlap and complement each other. For example, understanding the properties of geometric shapes makes it easier to move them around and specify their location in space. The teacher should support students to make connections between these two Big Ideas and between related concepts and everyday experiences.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Géométrie et sens de l'espace, Fascicule 1, p. 5-18.

Measurement Fundamentals (E2)

Measurement marks out our activities and, by the same token, guides our thoughts, our decisions and our perception of the world. It is so much a part of our daily activities that we forget its presence and importance. For example, we regularly ask ourselves questions such as 'Can this object fit through the doorway?', 'Which box could hold all these objects?', 'Which of these two destinations is closer?', without necessarily thinking that we are using a measurement.

In any situation, it is possible to measure different characteristics of an object. It is therefore important to specify which characteristic, commonly called attribute, is being measured. Here are some examples of measurable attributes that can be quantified by various non-standard and standard units of measurement.

Attribute: particular character of a being, of a thing

Measurement is complex and involves skills that go beyond the ability to measure with a measuring instrument or tool such as a ruler, measuring (graduated) cylinder, stopwatch, or thermometer; students must also learn to recognize and understand the meaning of measurable attributes of an object, to estimate their magnitude, and to measure them in a variety of contexts. Students benefit from having authentic measurement embedded in their learning experiences, as they solve a variety of real-life problems and make informed decisions.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 5-6.

The goal of measurement instruction in the junior grades is to develop students' understanding of measurement concepts, relationships and procedures. To achieve this goal, teachers should provide students with authentic learning situations that support the development of measurement skills and the acquisition of some essential measurement skills (these will be discussed in the Math Skills section).

For some students, measurement skills appear to be innate, as if they are inherited at birth. However, research shows that students can develop measurement skills through activities that incorporate the manipulation of concrete materials and the use of non-standard and standard units of measurement. The development of measurement skills goes beyond learning skills and procedures related to the act of measuring. It is a structured and organized path that evolves and must be adapted to the various measurable attributes of an object.

Buys and de Moor (2005) point out that the primary goal of measurement instruction is to develop a sense of measurement, and that to achieve this goal, teachers should support students to:

• recognize everyday situations that call for measurement;
• develop the ability to distinguish the different measurable attributes of an object and determine the situations in which to apply them;
• visualize the various units of measurement related to the different attributes;
• use measurement vocabulary correctly.

The measurement-savvy student is able for example, to estimate and determine the length of an object by comparing it with another object of a certain length or with some standard unit of measurement. To fully appreciate the significance of measurement literacy in the process of developing an understanding of measurement concepts, relationships and procedures, it is important to focus on the following three elements:

• spatial sense;
• benchmarks;
• estimation.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 7-8.

Measurement

Overview of Measurement

The learning content of Expectation E2 (Measurement) involves a large number of concepts. To help teachers plan and implement strategies that provide effective and coherent instruction, the key concepts are grouped under one Big Idea, Measurement Sense. This Big Idea is presented and developed in terms of three underlying key points: fundamental attributes and concepts, measurement relationships, and the act of measuring.

Big Idea - Measurement Sense

The exploration of various attributes, relationships, and procedures related to the act of measuring supports the development of measurement sense.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 35-36.

Ability to Visualize

---

The ability to visualize involves forming a mental image of a situation or an abstract concept. In measurement, this ability is mainly related to the ability to form a mental image of:

• certain measurable attributes;
• benchmarks associated with the various attributes.

Visualize certain measurable attributes: ability to form a mental picture of some measurable attributes helps students better understand their meaning. In the junior grades, students will develop the ability to visualize the attributes of length, area, capacity, and angle. Since time and mass do not represent something that can be seen or illustrated, students can at best form a mental picture of a few appropriate benchmarks for them.

For length, students will need to visualize a straight line or curve in a one-dimensional space. For example, in a situation where the length of a rectangular prism is to be determined, they need to visualize that they are determining the left to right measurement of the edge of the prism that has been labelled length.

Students should also recognize that in some situations the length attribute may take another name, for example:

• the height of a mountain;
• the width of a prism;
• the thickness of a cake;
• the height of a person;
• the depth of a lake;
• the perimeter of a box.

For area, students will need to visualize the interior space of a three-dimensional object. For example, when they are asked to determine the capacity of a prism is, they should visualize how much that prism can hold. 

Students should also recognize that in certain situations, these concepts might be named differently.  For example:

• the acreage of land;
• the land area of a city.

For the capacity attribute, students will need to visualize a three-dimensional space, that is, a picture of the interior space of a container. For example, in a situation where the capacity of a prism is to be determined, they need to visualize that they are determining the measure of its interior space.

For angle, students must visualize between the two line segments that come together to form the angle. The distance between these sides is the measure of the angle.

Visualize benchmarks: the ability to form a mental image of benchmarks associated with the different measurable attributes helps students estimate the measure of an attribute and check the reasonableness of a result obtained from using a measuring tool or by applying a formula. For example, a student who uses the width of a door as a benchmark for 1 m can use this to estimate that the length of the teacher's desk is about 1.5 m.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 20-22.

In the junior grades, students continue to investigate the properties of two-dimensional shapes and three-dimensional objects through construction activities (for example, building with a geoboard, straws, playdough, cardboard, interlocking cubes) and representation on paper (for example, representation on graph paper, dot paper).

These activities help students to be able to construct a mental image of two-dimensional shapes and three-dimensional objects based on specific properties and therefore promote the development of visualization skills.

As with angles, it is necessary for teachers to show and represent two-dimensional shapes and three-dimensional objects in a variety of ways so that students do not develop a single mental representation.

For example, students should recognize that each of the two-dimensional shapes below represents a trapezoid.

In order to construct a good mental image of three-dimensional objects, students must be able to visualize their two dimensional faces in two-dimensional space and as solids in the three-dimensional space.

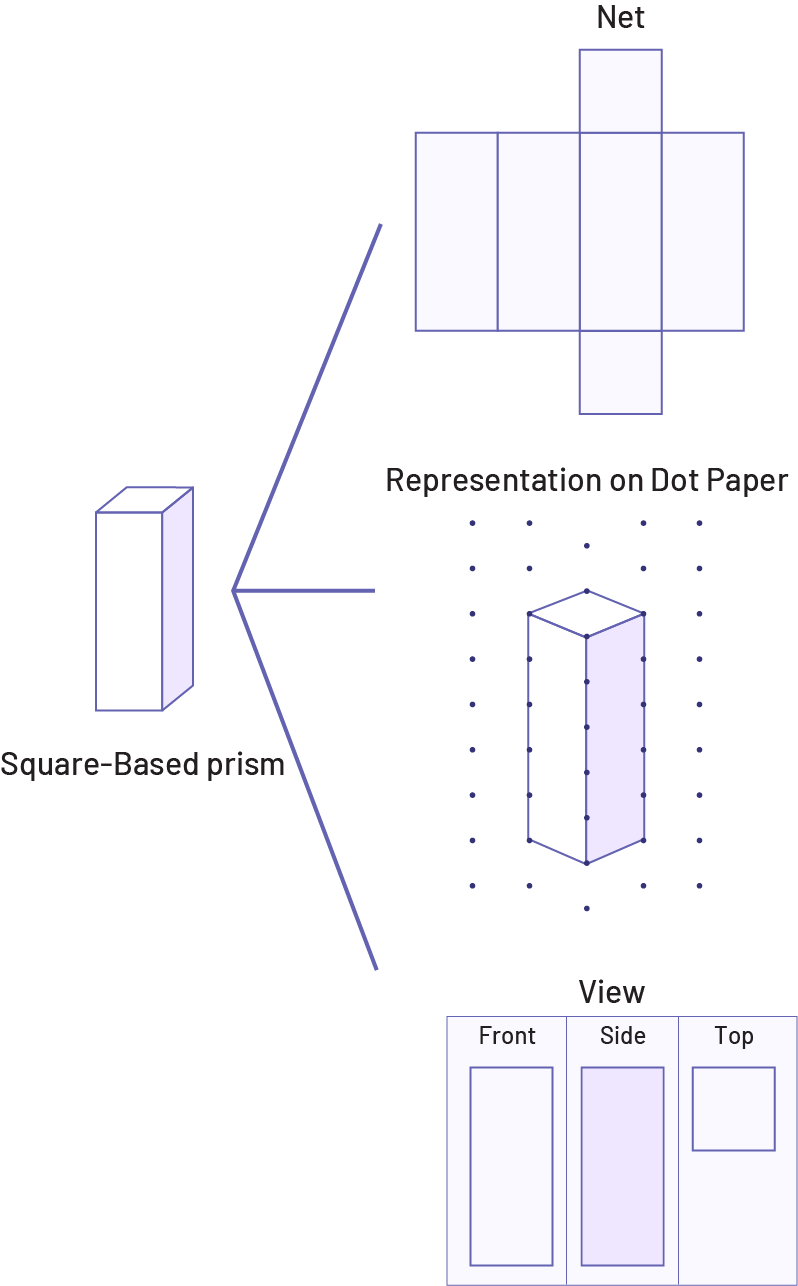Image A square base prism, and the development of that prism. Also, its representation on a dotted sheet. The view from the front, from the side, and from the bottom of that prism.

To help them develop the ability to move from one dimensional representation to another, and to consolidate their knowledge of the properties of three-dimensional objects, teachers should assign various construction activities (for example, constructing a model using cubes, constructing a three-dimensional object from a given net) and various representation activities (for example, drawing the net of a three-dimensional object, associating a three-dimensional object with its net or its top, front and side views).

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Géométrie et sens de l'espace, Fascicule 1, p. 28-30.

Spatial visualization is developed by mobilizing certain spatial skills listed by John Del Grande (1990), including mental rotation.

(John Del Grande, 1990. © 2019, National Council of Teachers of Mathematics. The Arithmetic Teacher, vol. 37, no. 6.)

Source: translated from Guide d'enseignement efficace des mathématiques de la 7^e à la 10^e année, Mesure et géométrie, Fascicule 3, p. 12-13.

Ability to Solve a Problem Situation

---

The ability to solve problems is an essential process in learning measurement. To help students develop this skill, teachers must present them with various types of problem situations in a meaningful context. It must encourage them to call upon their previous knowledge as well as their literacy and problem-solving strategies, to clearly communicate their results and to discuss the ideas of their peers during mathematical conversations. By being thus engaged in a reflection on the targeted concepts, the students will clarify the concept’s meaning.

Measurement problem situations should contribute to students' understanding of fundamental attributes and concepts, relationships, and the act of measurement. It is essential that students be actively involved in problem solving and subsequent discussions. These varied experiences allow them to develop their sense of measurement.

Example

Give students a small cardboard measuring 1 cm² and a copy of the rectangles below. Ask them to determine, using the square, which rectangles have the same area.

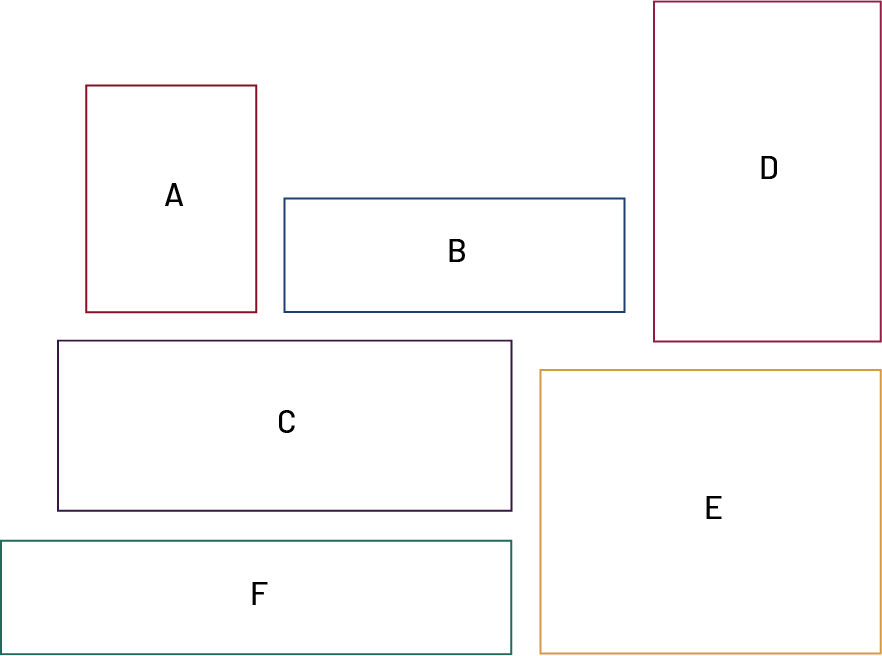
During the math exchange, teachers encourage students to justify their answers by asking questions such as:

• What strategy did you use to determine that Rectangles C and D have the same area? (I used the small cardboard as a unit of measurement. I lined up this cardboard 8 times on one side of Rectangle C and 3 times on the other side, so to cover it completely, I would need 8 columns of 3 cards. For Rectangle D, I found that I would need 4 columns of 6 cards. In both cases, it would take 24 cards to cover the rectangles, so their area must be the same).
• Can you think of another way to show that the area of these two rectangles is the same? (If we cut rectangle C vertically down the middle and place the two halves on rectangle D, we see that rectangle D is completely covered. This proves that the area of the two rectangles is the same).

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 23-24.

Reasoning Skills

---

Reasoning is a mental process in which ideas flow logically together. It is an important skill because it allows students to structure their thinking by integrating knowledge and establishing relationships among them. In measurement, there are many relationships to be established (for example, relationships among attributes, relationships among units of measurement). The skill of reasoning in a measurement context allows students to analyze the similarities and differences among measurable attributes, to draw conclusions, and, ultimately, to reinvest this knowledge in a new context or situation. By asking them to justify their reasoning and explain their problem-solving process, teachers take advantage of their intellectual curiosity to get them to go beyond the simple answer and to think about the fundamental concepts specific to each attribute. 

To help students develop the ability to reason in measure, teachers should ask open-ended questions and provide varied and complex problem situations. They should encourage students to:

• concretely represent their reasoning by showing their thinking;
• explain their approach and justify their results;
• observe and analyze the strategies used by other students.

Example

Teachers can present the following situation:

Marilou hikes for 3 km along a trail, starting at 9:42 a.m. and finishing at 11:00 a.m. How long does it take her to complete the hike?

To help students develop the skill of reasoning, teachers can ask questions such as:

• You say she did the hike in 78 minutes. How might you justify your answer?
• What approach did you use to solve the problem?
• How is this approach different from the one presented by the previous student?
• How is your approach different from the (student’s name) approach?

Teachers sometimes tend to ask students to justify their answers only when they are wrong. As a result, when students are asked to justify an outcome, they are led to believe that they have made an error. It is therefore important to regularly encourage them to justify their answer, whether it is correct or not. In this way, students will understand that this is simply a step in the process of reasoning.

Questions from teachers and suggestions from peers during mathematical conversations can help students to:

• realize that it is possible to solve the given situational problem in other, sometimes simpler, ways;
• formulate their reasoning;
• make more complex conjectures and generalizations.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 25-26.

The nature of students' mathematical reasoning is closely related to their ability to abstract. At Levels 0 and 1, students use mostly inductive mathematical reasoning, that is, reasoning from the particular to the general. Thus, when they manipulate a limited number of similar geometric shapes and objects and observe the attributes or properties of these shapes and objects, they attribute these characteristics to the set of geometric shapes and objects that are part of the same family. For example, after manipulating a small number of pyramid-shaped objects, students may conclude that all pyramids have a pointed end.

In the Junior Division, students gradually move from inductive reasoning to informal deductive reasoning, or from reasoning that is general to more specific. This type of reasoning allows them to draw certain conclusions about any geometric shape or object from known properties. For example, after recognizing that drawing one of the two diagonals of a rectangle results in two congruent triangles, students can deduce that the area of each of these triangles is equal to half the area of the rectangle (see figure below).

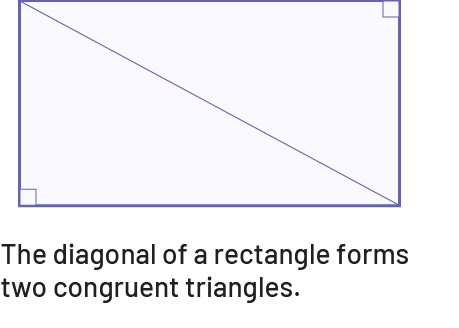Image The diagonal of a rectangle forms two congruous triangles. We see the rectangle with the diagonal and the marks of square angles.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Géométrie et sens de l'espace, Fascicule 1, p. 36.

Communication Skills

---

Communication is an essential component of learning mathematics. It is a skill that goes beyond the appropriate use of mathematical terminology and symbols in verbal or written communication. It is also, more importantly, a vehicle through which students develop an understanding of mathematical concepts in contexts that involve mathematical reasoning and arguments. This is what Radford and Demers (2004) call the conceptual dimension of communication.

These researchers also emphasize the importance of taking into account the social dimension of communication, or 'exchange' of ideas between two or more people. These exchanges are beneficial for all those involved when there is a culture of respect and listening to what others say.

To increase the effectiveness of geometry instruction in the classroom, teachers should foster a culture that values the exchange of ideas as a means of learning. They should also provide students with multiple opportunities to discuss their conjectures with their peers and to formulate clear and convincing mathematical arguments.

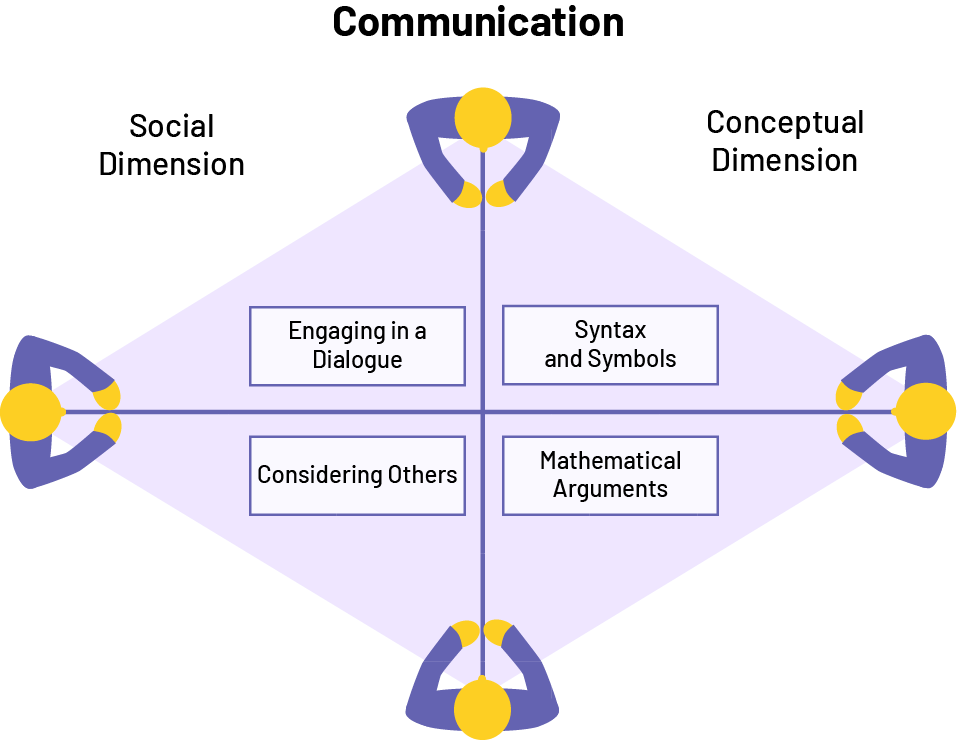Image Infographic named: communication. Four people are sitting at a table. They are each sitting at a corner of a diamond-shaped table. Above to the left, we can read: social dimension. Above to the right, we can read: conceptual dimension. The people sitting across from each other are linked by a blue line. This divides the table in 4 parts. These parts represent an idea: syntax and symbols; mathematical arguments; considering the others; engaging in a dialogue.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Géométrie et sens de l'espace, Fascicule 1, p. 8-9.

The ability of students to present a mathematical argument reflects their level of thinking. According to Radford and Demers (2004), students in the Primary Division typically begin constructing mathematical arguments using causal terms such as 'then' or 'because'. However, since they have not always fully understood the notion of causality, they sometimes use these terms incorrectly to justify a conclusion or the solution to a problem (for example, 'It's a square because it looks like a square.'). Teachers can help students develop the ability to use causal terms by giving them the opportunity to respond critically to arguments presented by other students (for example, 'Matéo says it's a square because it looks like a square. Do you think that's a clear and convincing argument?').

In the junior grades, students are more able to present a mathematical argument by correctly using causal terms (for example, 'The shape is a square because it has four congruent sides and four right angles.') They also begin to use logical consequence terms such as since...then or since...therefore (for example, 'Since any quadrilateral that has four right angles is a rectangle and all squares have four right angles, then all squares are rectangles.'). Although students are not yet able to present a formal, rigorous proof, they can appreciate the logic of a good mathematical argument.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Géométrie et sens de l'espace, Fascicule 1, p. 37.

For communication to occur, there must be an intention, a situation, a context, a code, a message and an explicit or implicit interaction between people.

The ability to communicate about measurement develops primarily in the context of problem solving or mathematical discussion. In any situation that involves reasoning and mathematical argument, communicating their thinking allows students to develop their understanding of concepts. The social dimension of communication plays an important role in the acquisition of this skill and benefits everyone involved in the act of learning about measurement. In the Primary and Junior grades, oral communication is a prerequisite for written communication.

Oral Communication

Oral communication is the most natural form of expression used by students. Speech remains the most useful and frequent means of communicating on a daily basis. It is essential to the transmission of ideas, discoveries, approaches and outcomes in measurement. It serves as a lever for students' thinking and engages them in structured dialogue that helps them make sense of their explorations. In order for students to develop this skill, they must be provided with a variety of opportunities to express themselves and demonstrate their understanding of different concepts.

In the junior grades, in team learning situations and mathematical exchanges, students will use vocabulary related to attributes and standard units of measurement. For example, students might describe a sandbox by saying, 'The perimeter of the sandbox is 12 m and the perimeter of the play area is 24 m.' They might compare objects to using appropriate terminology. For example, they might say, The mass of the book is greater than the mass of the pencil. Teachers may need to guide students in the use of correct vocabulary. For example, if a student says, 'My book is bigger than yours,' teachers should prompt the student to clarify by asking if their book is thicker, longer, or wider than yours.

In order to promote oral communication among students, teachers should reduce the length and frequency of their own input and allow time for student discussion and analysis of ideas, either as teams or individually. Before taking a response to a question, teachers should encourage think time and or group discussion and allow sufficient time for reflection. 

In conjunction with speech, students' gestures can contribute to communication by demonstrating the strategy used to solve a problem or the understanding of a concept in action.

Example

Two students demonstrate how they use a graduated cylinder to determine which of three containers has the smallest capacity.

Written Communication

Written communication is an excellent way for students to clarify their ideas and describe their problem-solving strategies. It also gives insight into what they have learned. Students often reveal much of what they have learned and mastered through their written work. Teachers should encourage students to leave as much evidence about their thinking as possible.

Example

Teachers present students with the following problem.

Mr. Burn has 24 m of masking tape to mark out a rectangular play area on the gym floor. He realizes that he could construct several different rectangles, so he decides to draw some of the rectangles on graph paper using a scale of 1 cm to 1 m. Draw some of the rectangles that Mr. Burn could draw, making sure that the perimeter of each one is 24 cm. Then determine the area of each rectangle. Keep track of your work.

Some students leave traces of their mathematical thinking with drawings only; it is important to get them to show their understanding and learning with words, phrases and sentences so that their reasoning and proving becomes more organized, clear and precise.

To help students improve the presentation of their written solution, teachers should encourage them to discuss the task at hand, anticipate possible solutions, and use concrete materials and familiar symbols. Several tools support the improvement of written communication (for example, word wall, organizational tool, math journal, interactive board).

In summary, written communication allows students to:

• record their learning and the development of their mathematical thinking in a portfolio or mathematics journal;
• take the time to think and organize;
• objectify certain concepts;
• enjoy a space for personal expression.

It also allows teachers to assess students' understanding of concepts and to better plan future learning activities. 

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 27-31.

Ability to Abstract

---

In the primary grades, students' geometric thinking is generally at levels 0 and 1. At first, students will learn to recognize geometric shapes and objects, name them and list some of their physical attributes (for example, the sphere is round and rolls). Many then construct a mental representation of geometric shapes and objects by associating them with known objects (for example, a rectangle looks like a door, a sphere looks like a balloon). In some cases, this representation is so entrenched that it prevents them from conceiving of an orientation of the shape or object other than the one that corresponds to it. See the figures below.

Image Students associate a rectangle to a known object, for example, a door. The text is accompanied by a drawing of a rectangle and its square angle. This figure doesn’t correspond with the image of a rectangle that certain students imagine. The text is accompanied by a drawing of a rectangle and its square angle in an oblique posture.

Later, students gradually move away from references to physical attributes and known objects as they learn to describe geometric shapes and objects in terms of their properties.

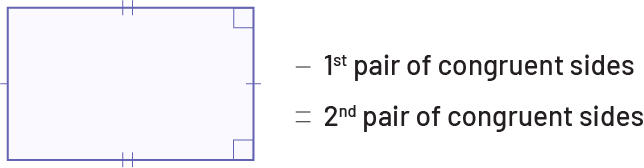Image A rectangle with dashes on the parallel sides and the square angles. A dash, first pair of congruous sides. 2 dashes, second pair of congruous sides.

In the junior grades, students' geometric thinking progresses to level 2 as their capacity for abstraction develops. This capacity is related to the ability to focus on certain properties in isolation. It allows them, for example, to use properties of a geometric shape or object to define it. Teachers can help students develop this ability by providing a variety of learning situations, such as:

• Learning situations that involve one or two specific properties

For example, teachers can ask students to construct on a geoboard or draw on dot paper a quadrilateral that has four congruent sides and at least one right angle. By comparing their results, students will see that all the resulting shapes are squares and may conclude that the definition of a square is simply that it is a quadrilateral that has four congruent sides and at least one right angle.

• Impossible learning situations

For example, teachers can ask students to construct on a geoboard or draw on dot paper a triangle that has three congruent sides and one obtuse angle. They will see that this is impossible and may conclude that an equilateral triangle cannot be obtuse.

• Learning situations that require the simultaneous consideration of more than one geometric shape

For example, teachers may ask students to construct on a geoboard or draw on dot paper a quadrilateral that is both a rhombus and a rectangle. Taking into account the properties of each of the two shapes, students will see that the shape is necessarily a square and may conclude that it is possible to define a square as a rhombus that has four right angles or a rectangle that has four congruent sides. This type of situation allows students to classify geometric shapes hierarchically (Figures 17 and 18) in order to highlight the relationships of inclusion (for example, all rectangles are part of the parallelogram family, but not all parallelograms are part of the rectangle family) and exclusion (for example, an acute triangle cannot be obtuse and vice versa).

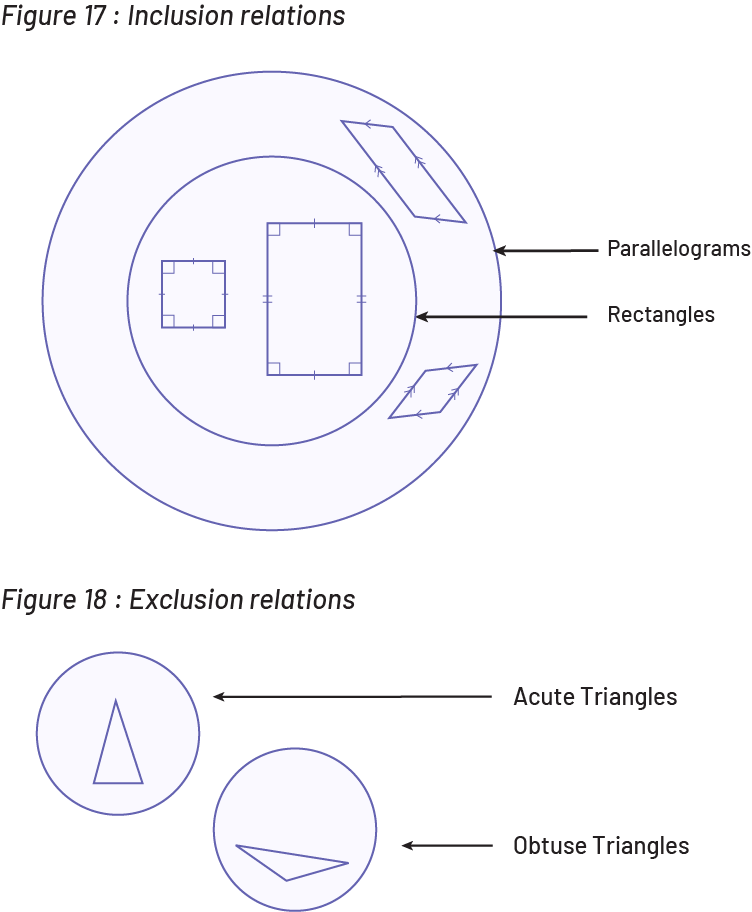Image Inclusion relations: Two circles, one is in the other. The larger one represents a set of parallelograms, examples are drawn. The smaller circle is a set of rectangles. Exclusion relations: Two circles are represented, individually. The first represents the acute triangles, the second represents the obtuse triangles. An example is placed in each circle.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Géométrie et sens de l'espace, Fascicule 1, p. 32-34.

Teachers should encourage students to go beyond the application of procedures and the use of measuring instruments so that they can develop a good conceptual understanding of the attributes of measurement, the corresponding standard units, and geometric properties, and to make connections between concepts, procedures, and relationships in measurement and geometry.

To do this, teachers should: 

• select effective teaching and learning strategies;
• strategically select the lines of inquiry;
• plan and structure the mathematical exchange;
• create a learning environment that is conducive to the development of a spatial sense.

Selecting Effective Teaching and Learning Strategies: a teaching strategy is defined as a way of doing things, an approach, a series of actions and means that teachers use in a given context. Effective teaching in spatial sense leads students to:

• think about attributes and relationships;
• solve measurement and geometry problems, both in real-life and purely mathematical contexts;
• demonstrate motivation and commitment to solving these problems;
• discuss their trials, possible solutions, and their understanding of concepts and procedures.

Strategically Select Lines of Inquiry: in order to help students develop mathematical thinking that reflects spatial sense, teachers must ensure that the questions they ask are appropriate to the time, situation, and level of student understanding by choosing questions that help students deepen conceptual understanding, make connections, propose conjectures, and make generalizations.

Planning and Structuring the Mathematical Exchange: throughout a learning situation, teachers plan how the consolidation activity or mathematical exchange will unfold by carefully observing student work and determining, based on one or more learning goals, which work should be presented to the whole class. This work should prompt discussion and help students consolidate their understanding of the intended concepts. For example, student work may be selected and displayed to highlight and compare:

• problem-solving strategies used by students (for example, illustrate the variety of strategies used or illustrate the same strategy presented in different levels of structure and organization);
• the materials used by students (for example, illustrate the difference between a representation made with drawings and one made with a ruler, rectangular layout, or symbols);
• the clarity of the proposed solution (for example, illustrate the difference between a partial representation of a solution and one in which students have organized, shown, and explained their solution clearly using words and symbols).

During the mathematical exchange, teachers should structure the exchange by leading discussions and making strategic interventions. Teachers should ensure that the concepts being discussed are clear and understood by the students. If necessary, teachers can conclude the mathematical exchange by modelling an effective approach, strategy, or procedure. This modelling can be done either by teachers or by a team of students. A well-structured mathematical exchange allows students to consolidate their knowledge and understanding of concepts and procedures and to recognize the importance of effective communication.

Creating a Spatial Sense Learning Environment: A learning environment conducive to a developing spatial sense is one that focuses as much on developing conceptual understanding of geometric properties, attributes, and units of measurement as it does on understanding procedures. Teachers should consciously use a variety of situations in both mathematics and other subjects that involve measurement as well as geometry. It is through regular exposure to the need to measure and perform various geometric experiments, in a variety of situations, that students understand the importance of measurement and geometry and develop the skills required to achieve them.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 31-34.