E1.1 Sort three-dimensional objects and two-dimensional shapes according to one attribute at a time, and identify the sorting rule being used.
Skill: Sorting Three-Dimensional Objects and Two-Dimensional Shapes
Sorting requires one to group items according to a certain attribute or characteristic (for example, shape, size, or colour).
In Grade 1, students will sort three-dimensional objects and two-dimensional shapes according to one attribute (for example, size, area, or colour) at a time.
When students can identify similarities and differences, they can sort objects, two-dimensional shapes, or three-dimensional objects according to an attribute (for example, size, area, or colour) using, for example, two hoops or two boxes.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 34.
Different Ways to Sort Three-Dimensional Objects
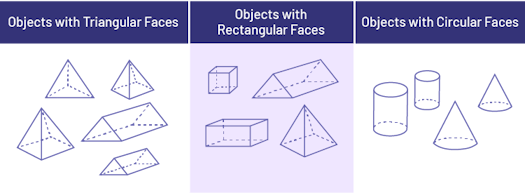
Types of Two-Dimensional Shapes to Include Sorting in a Classification Activity
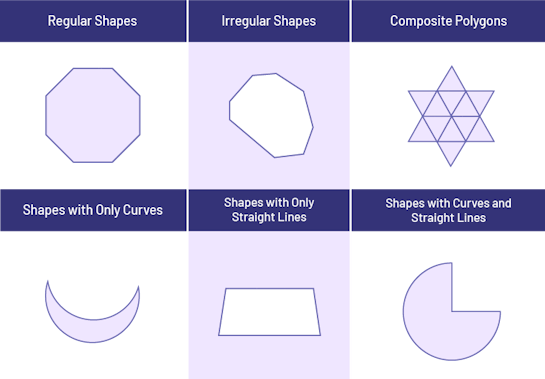image 3 columns table and 2 rows. The first column, first row: « Regular plane shapes. » the second column, the first row: « Irregular plane shapes. » the third column, first row: Decomposable (or composite) plane shapes. » The first column, second row: « Shapes holding only curved line planes. » The second column, second row: « Shapes holding only straight line planes. » The third column, the second row: « Shapes holding both straight- and curved-line planes. »
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Once the students have sorted several shapes according to a given criterion or rule, the teacher should ask them to sort two-dimensional shapes or three-dimensional objects using their own sorting rule.
During consolidation, teachers should focus students on the properties common to all shapes in the same class to support them in distinguishing between properties that are important in identifying a two-dimensional shape or three-dimensional object, and those that are not.
Over time, the students realize that families of geometric shapes have common properties (for example, all triangles have three sides) and that subsets have distinct properties (for example, some triangles have two equal sides).
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 35.
Knowledge: Geometric Property
A geometric property is a particular attribute of a two-dimensional shape or a family of two-dimensional shapes, or of a three-dimensional object or a family of three-dimensional objects.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 32.
In Grades 1 to 3 , students must continually redefine their mental image of a two-dimensional shape or three-dimensional object, as their mental representation is often limited to the one most often presented or to a stereotypical representation. A variety of representations of geometric shapes helps students understand the invariance of shape properties, regardless of material, size, orientation, perspective, etc. For example, any two-dimensional shape with four congruent sides and four straight sides is a square.
It is important, therefore, that during directed mathematics activities, teachers take the opportunity to present a wide variety of representations of:
- geometric shapes;
- two-dimensional shapes of different sizes and orientations;
- photos of objects from various perspectives;
- drawings of three-dimensional objects reproduced in different ways.
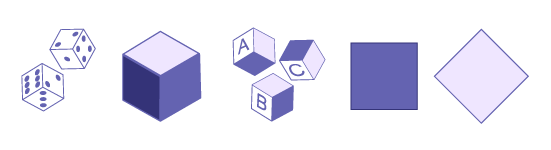
Some children can picture certain two-dimensional shapes and three-dimensional objects, but are not yet capable of reversible operations (such as rotation). As soon as the orientation of a rectangle or cylinder, for example, is changed, they tend to think that it is no longer the same figure or three-dimensional object. The child does not understand that certain topographical changes do not change the measurable attributes of the two-dimensional shape or three-dimensional object.
Example 1
Some students believe that the first square is a proper square while the second is not a square, since their mental image of the square is the one most frequently presented to them (on the left).
They will need support to recognize that a cylinder remains a cylinder, even if it is placed differently. In either orientation, the object always has a planar face in the shape of a circle and a curved surface.
Example 2
Some students believe that the first cylinder is a proper cylinder while the second is not a cylinder, since their mental image of the cylinder is that of a cylinder standing on its base (on the left).
They must therefore be brought to realize that a cylinder remains a cylinder, even if it is placed differently. The solid always has a planar face in the shape of a circle and a curved surface.
Example 3
To confirm the student's mental representation of a two-dimensional shape or three-dimensional objects, teachers can use the strategy of examples and non-examples. This strategy requires the student to recognize an object, two-dimensional shape, or three-dimensional object using characteristics or properties and to eliminate other an objects, two-dimensional shapes or three-dimensional objects that do not have these characteristics or properties. In the following example, the term waline is made up, and refers to triangles.
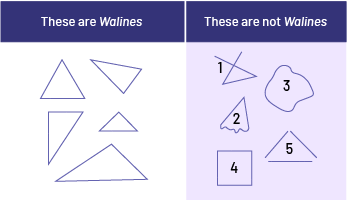
Figure 1: This figure is not a waline, because it is not a triangle. Figure 1 is formed by an open broken line, while a triangle is always formed by a closed broken line.
Figure 2: This figure is not a waline, because it is not a triangle. Figure 2 is formed by a curved line and a broken line, while a triangle is always formed by a closed broken line.
Figure 3: This figure is not a waline, because it is not a triangle. Figure 3 is formed by a closed curved line, while a triangle is always formed by a closed broken line.
Figure 4: This figure is not a waline, because it is not a triangle. It is a square. A square is also formed by a closed broken line, but it has four sides, four vertices and four angles.
Figure 5: This figure is not a waline, because it is not a triangle. It is three straight lines that form an open shape. A triangle is a closed shapebecause it is not a triangle. It is three straight lines. A triangle is always formed by a closed broken line.
It is important to ask the student not only to circle or recognize the walines, but also to explain their choice. This is to check their understanding of the concept of a triangle and offer more support, if necessary.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 36-38.
Knowledge: Attribute
From the time they enter school, children recognize, name, compare, and sort objects using observable attributes. They can identify and describe objects using vocabulary related to characteristics of such attributes as size (for example, big, small, long, short, thick, thin), colour (for example, red, blue), texture (for example, soft, rough, silky, smooth), movement (for example, rolls, slides), purpose (for example, to build a tower, to make a mosaic), and type of material of objects (for example, plastic, wood). These terms are part of the child's everyday vocabulary.
The child visually identifies similar or different attributes between objects and readily distinguishes shapes of familiar objects, so they are able to identify, name, compare and sort objects by observing similarities and differences in their appearance.
Through observation and manipulation, the aim is to get the child to identify, name, compare and sort objects as well as geometric shapes by first using words that they know and by using mathematical vocabulary related to geometric properties (number of vertices, number of faces, number of sides, number of edges, type of angles, type of lines, lines of symmetry).
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 32.
Knowledge: Sorting Rule
The following are examples of sorting rules that can be used by students.
- Two-dimensional shapes formed by a broken closed line
- Two-dimensional shapes formed by a closed curved line
- Two-dimensional shapes that have three sides
- Two-dimensional shapes that have four sides
- Two-dimensional shapes without sides
- Three-dimensional objects that have only faces
- Three-dimensional objects that have faces and surfaces
- Three-dimensional objects that have only surfaces
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 35.