La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E1.2 Compose and decompose two-dimensional shapes, and show that the area of a shape remains constant regardless of how its parts are rearranged.

Skill: Composing and Decomposing Two-Dimensional Shapes

By the time they begin school, most students are able to identify examples of shapes in their environment. Students also know that the shapes they recognize are rarely isolated, and that many shapes are part of larger shapes or objects. For example, if asked to find rectangles in the classroom, students might also notice that the window is made of rectangular glass panels or that the lid is part of a box where the sides and bottom are rectangles.

Instructions should go beyond identifying two-dimensional shapes and three-dimensional objects to supporting students in understanding the physical relationships between shapes and how shapes can be assembled (composed) from or decomposed into other shapes. Structure-building activities that require students to use geometric shapes such as pattern blocks or tangram pieces to create new shapes by composing or decomposing encourage students to think about how geometric shapes fit together for functional (for example, designing a machine) and aesthetic purposes (for example, creating a model).

Picture-making by combining shapes is beneficial in promoting student reflection and discussion about two-dimensional geometry. Young children move through developmental stages (outlined below) in combining shapes to make composite shapes (Clements, 2004b). Although approximate ages are provided for each level, progression through these stages is largely the result of experience. Teachers play an important role in providing picture-making activities and in demonstrating to students how shapes can be combined in increasingly complex ways.

Stages of Development for Composing 2D Shapes (Clements)

  • Precomposer (approximate age: 3 years) 
    Children use individual shapes to represent objects or persons but are unable to combine them to compose a larger shape. For example, children might use three separate shapes to represent the sun, a slide and a sandbox.
Three plane figures: a hexagon, a triangle and a square.
  • Piece assembler (approximate age: 4 years)
    Children combine shapes to make a picture in which each shape represents a part of an object or person (for example, a rhombus is used for a leg). Like the precomposer, the piece assembler perceives shapes only as wholes and sees a few geometric relationships between shapes or parts of shapes.
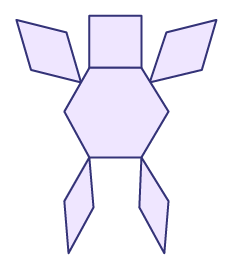
A character that has body parts drawn with flat figures. The head is a square. The body is a hexagon. The arms and legs are diamonds.
  • Picture maker (approximate age: 5 years)
    Children assemble shapes to form pictures in which several pieces are used to represent part of an object (for example, three squares for a body). Children use trial and error to create new shapes.
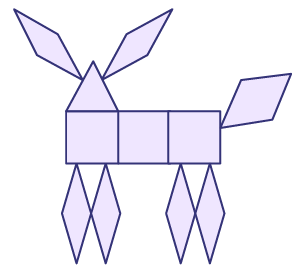
An animal that looks like a horse and the body parts are drawn with flat figures. The head is a triangle. The body is made of 3 triangles. The ears and the tail are diamonds. The four legs are diamonds.
  • Shape composer (approximate age: 5 years)
    Children combine shapes intentionally, knowing how shapes will fit together.
A teddy bear-like animal whose body parts are drawn with flat figures. The head is a hexagon. The ears are diamonds. The body is a hexagon. The arms and legs are formed with two rhomboids, per limb. The feet are formed with a rhombus..
  • Substitution composer (approximate age: 6 years)
    Children form composite units of shapes and are able to substitute some shapes for others (for example, six green triangles for a yellow hexagon using pattern blocks).
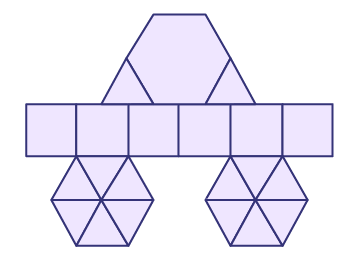image A vehicle is made of flat shapes. The upper part is made of a hexagon, two triangles are placed one on the right and the second on the left, to serve as a base for the upper part. The central part is made of 6 equal squares that are aligned. The lower part represents the wheels. Each wheel is made of 6 triangles that form a hexagon.
  • Shape composite repeater (approximate age: 7 years)
    Children construct a composite unit of shapes and intentionally repeat the the unit.
3 shapes composed of flat shapes, each of which looks like a tree. They are all three identical. The trunk is made of a square. The body of the tree is made of 9 triangles that are placed in such a way as to make a larger triangle.

Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 13-15.

Skill: Show That the Area of a Shape Remains Constant

In the Primary grades, fundamental concepts are essential to the development of an understanding of measurable attributes. Conservation is one of the fundamental concepts.

In measurement, conservation refers to the concept that the measurement of an attribute, in either non-standard and standard units, remains the same whether the object is moved, transformed, or decomposed.

It is important that teachers regularly ask students to transform, move, or decompose an object and compare the measurement of any attributes, in non-standard and standard units, before and after the transformation.

Students will be able to question each other, exchange ideas, and discover the circumstances in which the concept of conservation is applied.

An Example of Conservation of Area

The area of shapes 1 and 2 is the same as the area of the square, because all three shapes are constructed from the same seven pieces of a tangram set.

A student is at the board. He shows a poster with the title "Areas of Figures". There is a square, figure one looks like a house, figure two looks like the point of an arrow.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, Géométrie et sens de l'espace, p. 53

The student who understands this concept realizes that the area of a shape remains the same whether the shape is moved, transformed, or decomposed.

Example

Luke chooses two pentominoes and puts them together to create a shape. He draws this shape on graph paper and colours the squares that are part of this shape. He creates another shape with the same pentominoes. What can we notice about the area of Luke's two shapes?

On two grid spaces, two pentominoes are used to make a design. The two pentomino shapes are defined by the colors red and blue. In the first grid, the shape looks like a flower. In the second grid, the pentominoes are interlocked.

The area of each shape is identical; each occupies the same number of squares, but the pentominoes are arranged differently. The area has not increased or decreased; the area is still the area of the two selected pentominoes.

Additivity

Another fundamental concept for students to develop is that of additivity. Students who understand this concept realize that the area of a shape is equal to the sum of the area of each of its parts.

Example

On a geoboard, a student creates two adjacent rectangles. They estimate and measure the area of each rectangle. Using a different coloured rubber band, they join the two rectangles into a single shape. What do we observe when we compare the area of this new shape with that of the original shapes?

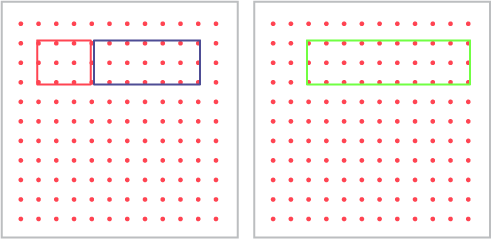
On a geoplan, a red rubber band represents a square. Following it, a blue rubber band represents a rectangle that has twice the area of the square. On a second map, a green rubber band represents the total area of the square and the rectangle.

The area of the new shape is equal to the sum of the area of the two rectangles combined. The area of the above example is: 6 square units + 12 square units = 18 square units.

Source: translated from Fiche de la maternelle à la 3e année Attribut, aire.

The same area can take an infinite number of forms.

Two areas can be compared directly by overlapping or matching them to determine which is larger.

To better compare two areas by making it easier to overlap and match them, one of the two areas can be decomposed and its parts rearranged to form a new shape. If the area remains the same, the comparison is valid.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Knowledge: Area

Area is a measure of the space inside a two-dimensional shape.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Students form a mental image of a flat or curved surface to find its area. For example, in a situation where the area of a given rectangle is to be determined, students need to visualize that they are finding the measure of the space occupied within the rectangle. Students should also recognize real-life situations that involves, for example:

  • the acreage of a piece of land;
  • the area of a city.

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3eannée, Géométrie et sens de l'espace, p. 21.

Example

I determine the area of the top face of the box by covering it with sticky notes.

Adhesive butterflies cover the face area of a box.

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3eannée, Géométrie et sens de l'espace, p. 46.

Example

Students demonstrate their understanding of area by covering the surface with pattern blocks.

The area of the surface is covered with geometric mosaics.

”I used four blue rhombuses, four green triangles and a yellow hexagon to cover the kite. The shapes don't overlap.“

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3eannée, Géométrie et sens de l'espace, p. 28.

Teachers ask questions such as:

  • What do you notice?
  • What is the area of the square? Is this an effective strategy for measuring area? What changes could you make?
  • Can you compare the area of your square with the area of another team's square? What do you notice?

The teacher's open-ended questioning supports students to deepen their understanding of the concept of area.The student needs to understand that in order to effectively measure the area of a two-dimensional shape, the units of measurement must be placed without spacing or overlap. When the two-dimensional shape is completely covered with different non-standard units, a conversion is necessary to determine one unit of measure. For example, in the previous image, the student may notice that the hexagon can be made with six triangles and each of the rhombuses can be made with two triangles. Therefore, the area is equivalent to 18 triangles .

The student modifies the pattern blocks used to measure the area of the square using only green triangles and making sure to leave no gaps or overlaps between the triangles.