E2.1 Choose and use non-standard units appropriately to measure lengths, and describe the inverse relationship between the size of a unit and the number of units needed.
Skill: Measuring Lengths with Non-standard Units
The second step in the act of measuring is selecting an appropriate non-standard or standard unit to measure the attribute.
To do this, it is important to choose a unit that reflects the attribute to be measured and is appropriate to the situation, and it is usually best to use the same unit.
Steps in the Act of Measuring
- determine the attribute to be measured;
- choose the unit;
- determine the measurement;
- communicate the result.
When first exploring an attribute of an object, it is best for teachers to encourage students to choose a non-standard unit of measurement first, so that they can focus on the attribute rather than the tool and the more abstract standard units.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Mesure, p. 83.
The third step in the act of measuring is to determine the measurement of the attribute for an object quantifying it in terms of a unit.
Depending on the situation, the student typically uses one of the strategies below to determine a measurement:
- compare and order;
- juxtapose units;
- use a measuring tool.
The choice of strategy depends on the context, the intended use of the measurement, the degree of accuracy sought, and the measuring tools available. For the purposes of this learning task, students will compare and order and juxtapose non-standard units.
Compare and Order
Comparing and ordering involves comparing two objects in terms of the same attribute. For example, to give an idea of the length of one's pencil, a student might compare the length of the pencil with the length of a pen and conclude, ”My pencil is a little longer than this pen.“ This strategy does not, strictly speaking, quantify the measurement of an attribute of an object; rather, it simply establishes an order of size for that attribute by establishing that it is larger or smaller than the same attribute of another known object. Note that all of us use this strategy in a number of situations in which we feel that quantifying the measurement is not really necessary.
For example, to ensure that a piece of wrapping paper is long enough to wrap a box, simply compare the perimeter of the box with the length of the paper by superimposing the four of the sides of the box, in succession, on the paper.
The measurement of an attribute of two objects is compared either by direct comparison or by indirect comparison.
- Direct Comparison
From an early age, children compare the measurement of an attribute of two objects by direct comparison (for example, the length of two chocolate bars, their own height relative to another child). They then communicate the result descriptively rather than quantitatively (for example,”this chocolate bar is longer than that one,“ ”I'm shorter than you“). Direct comparison is usually done either by placing one object on top of another, or by placing the two objects side by side or back-to-back.
Example
Students place two cereal boxes upright, one against the other, and notice that one box is higher than the other.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 89-91.
- Indirect Comparison
When a direct comparison cannot be easily made, a third object can serve as a “go-between” tool to make an indirect comparison. For example, one could use strides to measure the length of a school hallway and then compare that measure with the number of strides needed to walk the length of another hallway.
The ability to compare various attributes of objects through indirect comparison contributes to the development of the property of transitivity, so it is important that teachers encourage students to make a direct or indirect comparison of objects with as many attributes as possible.
Juxtaposing Units of Measurement
Iterating involves carefully placing a number of benchmarks units side by side to represent and determine an object’s length.
Example
A student determines the length of a cardboard box using small and large paperclips as units. They arrange a series of paperclips of each size to measure the distance from one end of the box to the other. They then count the paperclips used and conclude, for example, that the length of the box is equal to the length of 14 small paperclips or the length of 8 large paperclips.
Juxtaposing units quantifies the measurement of any given attribute of an object, usually in terms of non-standard units. This strategy is particularly useful in helping students develop their understanding of the attribute length, since the measurement of the attribute is expressed in terms of concrete benchmarks rather than more abstract standard units such as centimetres. It also allows students to better understand the concepts of iteration and structure associated with units.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 91-93.
Fundamental Concept: Structure Associated with Units of Measurement
The student who understands this concept realizes that units of length are juxtaposed in a one-dimensional space, without gaps or overlaps, to cover the distance between two ends of an object.
Example
”Four Grade 2 students measured the width of identical placemats with sticks, but had different results. Who measured accurately? Explain why.“
image Melissa's red placemat is measured with 5 small sticks that are slightly spaced.Celeste's purple placemat is measured with 6 small sticks that are slightly misaligned. Natasha's yellow placemat is measured with 3 larger sticks, they are perfectly placed. Eric's green placemat is measured with 4 large sticks that are misaligned
Natasha measured accurately, as she used identical sticks and placed them in a straight line along one side of the placemat with no gaps and no overlap.
Source: translated from Fiche de la maternelle à la 3e année Attribut longueur, p. 4.
Skill: Describe the Inverse Relationship Between Unit Size and the Number of Units Needed to Measure Lengths
The analysis of relationships, which is just as important in Spatial Sense as it is in Algebra, leads students to formulate a generalization. To do this, they can follow an informal process like this one:
Analyzing relationships allows students to develop their sense of measurement, as well as their understanding of standard units.
Inverse Relationship
The number of units it takes to determine an attribute is inversely proportional to the size of the units. In other words:
- the smaller the unit, the greater the count;
- the larger the unit, the smaller the count.
For example, if one student uses a tablespoon and another student uses a teaspoon to measure the capacity of a container, they discover that it takes more teaspoons than tablespoons because the teaspoon is a smaller unit than the tablespoon.
Example
The box is the length of 14 small paperclips, so if I measure the box with large paperclips, I will need fewer paperclips.
Although the concept of inverse relationship may seem obvious in this type of situation, it is problematic for many students who are more accustomed to direct relationship situations (for example, the greater the distance to be travelled by bus, the greater the travel time). In order to help them understand this concept, the teacher should present them with a variety of concrete measurement situations that encourage them to make this connection.
When students understand the concept of the inverse relationship between the number of units it takes to determine an attribute and the size of the units, they can more easily understand and establish relationships between some of the standard units of measurement, such as the metre (m) and the centimetre (cm).
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 60-61.
Knowledge: Non-Standard Units
A non-standard unit is not part of a uniform, recognized system, such as the metric system, so the interpretation of a non-standard unit of measurement may differ from person to person, given the subjective nature of the choice of unit (for example, saying that a length measures three erasers may be interpreted differently depending on which eraser a person uses).
Students can use a variety of non-standard units to measure lengths. Examples include:
- Everyday objects: length of a paperclip, a toothpick, a pen, a straw
- Personal benchmarks: finger width, height, foot length, hand size or arm length, strides
- In class: length of a ruler
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Length
Length is a measure in a one-dimensional space.
A length can refer to:
- the size of a line segment, namely the distance between two points;
- the distance between two parallel lines or two parallel planes;
- a perimeter;
- a height, a depth, a thickness, a width, a height (of a person).
Note: For some students, these different terms associated with length may be confusing. The term ”magnitude“ used in the description of the attributes length, area, and capacity refers to what can be estimated, evaluated, or measured.
Examples
image Two points connected by a straight line. Two points connected by a curved line. Two double arrows, green. They are parallel. Between them is placed a black double arrow, it is perpendicular to the other double arrows. An obstacle for the horses. An arrow is placed between the two vertical bases.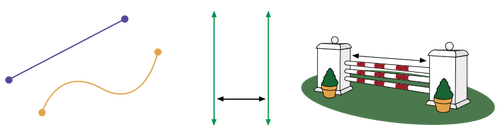
The perimeter is the length around a two-dimensional shape or three-dimensional object.
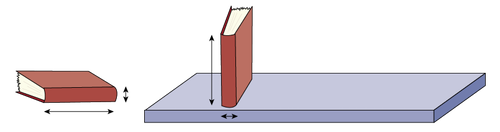image Two books. The first book is placed on its cover. An arrow shows the length of the book and another arrow shows its thickness. The second book is standing on a shelf, one arrow shows its height and a second arrow shows its thickness.
The length of a book becomes its height when stored upright on a shelf, just as its thickness becomes its width.
Source: translated from Fiche de la maternelle à la 3e année Attribut longueur, p. 2.
Knowledge: Fundamental Concept of Iteration
In measurement, iteration refers to the act of placing, repeatedly and in an orderly fashion, the same benchmark or unit in order to determine the measurement of an attribute. The number of times the unit is placed then corresponds to the measurement of the attribute.
Example 1
A hand can be used as a non-standard unit to measure the length of a table. Simply place the hand successively, without spacing or overlapping, to cover the distance from one end of the table to the other. One can then determine, for example, that the length of the table is equivalent to three hand lengths. This iteration allows one to visualize the relationship between the total length of the table and the length of the hand and gives meaning to the resulting measurement.
Iteration involves concrete action, and is particularly well suited to situations involving the attributes length and area.
Example 2
”How can you use the length of a straw as a unit to estimate and measure the height of a friend?“
(Successively place the straw, without gaps or overlaps, to cover the distance between the person's feet and head and determine the number of times the straw was placed.)
Source: translated from Fiche de la maternelle à la 3e année Attribut longueur, p. 2.
It is important that iteration be explored early in the teaching of measurement in order to properly construct this fundamental concept that allows students to understand that a quantity can be perceived not only as a whole, but also as a sum of smaller parts. Only after understanding this relationship between the part (the unit) and the whole (the attribute being measured) can students truly grasp the meaning of any measurement.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Mesure, p. 48-49.