E1.2 Compose and decompose two-dimensional shapes, and show that the area of a shape remains constant regardless of how its parts are rearranged.
Activity 1: Tangram (Compose, Decompose Geometric Shapes and Conserve Area)
Instructions
Give each student a square card.
Explain to students that they will be creating their own version of a tangram.
Explain what a tangram is, if necessary.
Specify that the square must be cut into at least six pieces.
Example
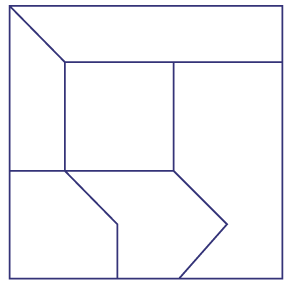
Ask students:
- to create another shape with the pieces of their tangram and draw the outline;
- exchange their pieces and the traced outline with another student who will try to recreate the shape.
Teacher Moves
Invite a few students to come and explain to the class how they went about recreating the shape.
Ask questions such as:
- What do you notice?
- What can you tell us about the area of the square box?
- If you compare the area of your tangram with the area of another student's tangram, what do you notice?
Point out that the square cardboard can be broken down into smaller two-dimensional shapes and put back together. The area remains the same, even if the pieces look different. The area remains constant no matter what tangrams are used. This is the fundamental concept of conservation.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Géométrie et sens de l'espace, p. 49-50.
Activity 2: Shapes in Order of Magnitude (Compare)
The teacher places six different irregular shapes on the four walls of the classroom, two pairs of which have the same area (see Appendix 1). The teacher provides the students with scissors, cardboard, string, post-it notes, pencils, and 1 cm x 1 cm grid paper (see Appendix 2). The teacher presents the following situation:
- In a math contest, the following challenge was given to participants, ”Without using a ruler, place the following shapes in order from the one with the smallest area to the one with the largest area.“
- You are allowed to bring only one shape at a time to your desk and you may not write on it.
- How can you solve this problem?
A mathematical discussion should follow this activity so that students can share their strategies. This activity encourages discussion and allows students to realize that several strategies can be adopted to solve the same problem.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca), p. 1.
