La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E1.3 Identify congruent lengths and angles in two-dimensional shapes by mentally and physically matching them, and determine if the shapes are congruent.

Activity 1: Identifying and Verifying the Congruence of Two-Dimensional Shapes

A wall in a classroom at the Frontier School has a particular pattern.

A grid represents a mosaic of multicolored squares
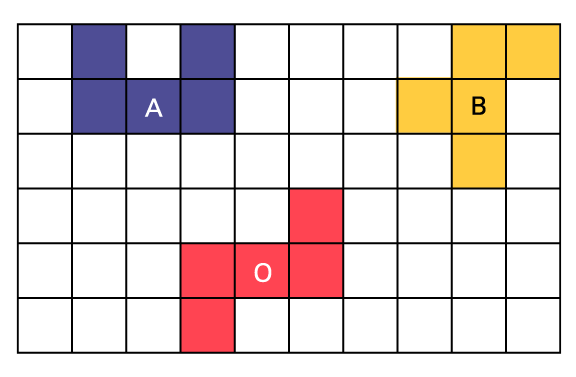
  1. There is a broken ceramic tile on the wall in the Grade 2 classroom. The custodian, Ms. Mireille, needs to find a tile to replace it. Which of these three tiles has properties congruent with the broken (white) tile?image A grid has 3 different shapes. The first one is called "A". It is composed of 5 blue squares. Placed in a "U" shape. The second is called "B". It is composed of 5 yellow squares, arranged as follows two squares side by side, next line two squares side by side, the second square of this line is under the first of the previous line. The fifth square is placed under the second of the second line. The third row is called "O". It is composed of 5 red squares. The first square is alone on its line. The next line has 3 squares, the last one is placed under the square of the first line. The last square is placed under the first square of the second line.
  2. The grade 2 class would like to add this design to their floor. Talia is creating a plan to propose to the school principal. She is missing one piece. She is not sure which one to choose. Help her choose the right tile.A mosaic composed of shapes of different colors. A space is empty in this mosaic. The empty space has 8 sides, the longest side is 3 centimeters.

    Tile 1

    Tile one: Shape of 7 sides of which the longest is 3 centimeters.

    Tile 2

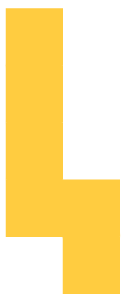
    Tile 2: 8-sided shape, no information about the length of the longest side.

    Tile 3

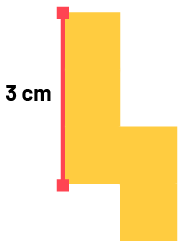
    Tile 3: shape with 8 sides, the longest of which is 3 cm.

  1. In the hallway, there is a piece of tile missing from the floor in one corner. Which one should be chosen? Explain your choice.Example of a tile with a missing triangular part. Four possible triangles of different sizes: "A", "B", "C", "D".

    Source: translated from En avant, les maths!, 2e année, ML, Sens de l’espace, p. 15-16.

Activity 2: Identifying and Verifying the Congruence of Two-Dimensional Shapes

Invite students to mentally superimpose flat shapes found in the classroom to determine if they think any are congruent. Then ask them to determine if the shapes found are actually congruent by superimposing them on top of each other or by creating a paper copy of one shape to superimpose on the other (transitivity). Give feedback on the shapes that are not congruent: did the student identify congruent lengths or angles that gave them the impression of congruence between the two shapes found?