At a Glance...

E2.9 Use square centimetres (cm²) and square metres (m²) to estimate, measure, and compare the area of various two-dimensional shapes, including those with curved sides.

Skill: Estimating the Area of Various Two-Dimensional Shapes, Including Those with Curved Lines

---

Estimation Skill

Adults, just as the students, must approximate sizes in a variety of everyday situations. In other words, they must estimate (for example, estimate the number of tiles needed to cover an area).

In measurement, estimating is a process based on visual information and prior experience that allows one to make a judgment about the approximate size of some attribute (for example, length, area, capacity, time) without resorting to a measurement strategy.

Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3^e année, Mesure, p. 16.

The square centimetre and square metre are used to quantify area, and although they are both basically squares, they can be broken down to any shape (for example, a square can become two triangles, or two-dimensional shapes with curved and straight lines, or four smaller squares).

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Skill: Measuring and Comparing the Area of Various Two-Dimensional Shapes, Including Curved Lines Using Square Centimetres and Square Metres

---

In Grade 3, students measure the attribute of area with non-standard units (for example, pattern blocks) and with standard units, such as square centimetres and square metres.

Examples

• Use square centimetres to estimate and measure the area of a variety of two-dimensional shapes, including polygons.

• Use square centimetres to estimate and measure the area of various two-dimensional shapes with curved lines.

• Tile a grid without gaps or overlaps. A square with a side length of 1 unit (a unit square) has 1 square unit of area. Any standard unit of length (metric or imperial) can produce a standard unit of area.
• Square centimetres and square metres are standard metric units of area.
• Area is measured by counting the number of full or partial units needed to cover a surface. For example, a surface that is completely covered by 18 unit squares has an area of 18 square units.
• Shapes chosen to represent square centimetres and square metres must retain a constant area, even if they are rearranged into a different shape or form. Tracking the count of partial units and combining partial units into whole units ensures that the measurement is as accurate as possible.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Fundamental Concepts

In the primary grades, fundamental concepts are essential to the development of an understanding of measurable attributes, including the concept of structure associated with units of measurement.

Structure Associated with Units of the area of a rectangle

The student who understands this concept realizes that the units of area of a rectangle must be juxtaposed in a two-dimensional space, without gaps or overlaps, to cover the rectangle in an array consisting of columns and rows.

Example

“How can Zoe determine the area of her library book using a sheet of graph paper?”

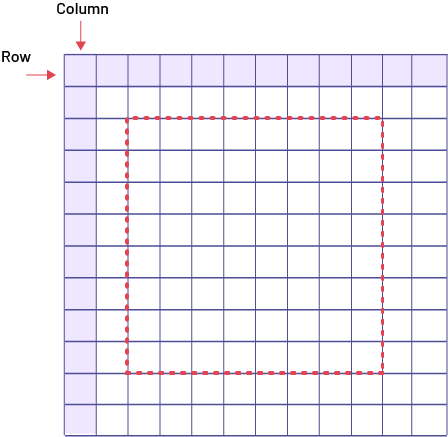
Zoe first draws the outline of her book on a sheet of graph paper. She then counts the number of columns (eight) and rows (nine) within the outline of the book. She then determines that the area of her library book is equal to 72 square units.

Relationships

By exploring the area of two-dimensional shapes, students begin to establish relationships between the dimensions of an object and its attributes.

Example 1 : Relationship between the dimensions of a rectangle and its area

In Grade 3, as students cover a rectangle with tiles or a transparent sheet of graph paper to determine the area of a placemat, teachers ask the following questions:

- If the horizontal sides of the placemat were longer, would I use more tiles, fewer tiles, or the same amount of tiles to determine its area?

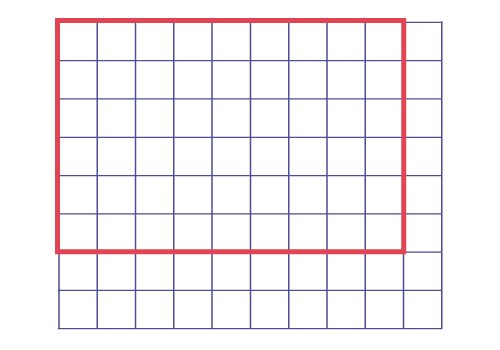
- If the vertical sides of the placemat were shorter, would I use more tiles, fewer tiles, or the same amount of tiles to determine its area?

Students discover that as the length of the base of a rectangle increases, its area increases (relationship between base and area).

Students discover that as the length of the height of a rectangle increases, its area increases (relationship between height and area).

This relationship can be demonstrated very well using an interactive board.

Example 2: Relationship between the dimensions of a rectangle and the number of columns and rows

To support students in making connections between the dimensions of a rectangle and its area, teachers help students observe the relationship between the number of units of length of a side and the number of square units in the row or column. For example, they present several rectangles on the board and ask students to determine the length of the base and then the number of square units in the row.

By making these observations, students will be able to more easily relate the measurements of the base or height to the number of rows or columns of a rectangle, and later, in the junior division, they will be able to better understand why the area of a rectangle can be determined by applying the formula A = b × h.

No Relationship

It is also important for teachers to provide students with activities that allow them to explore situations in which there is no existing relationship. This type of activity allows students to better understand the importance of testing a conjecture before concluding that it is true or making a generalization.

The examples below illustrate that some students mistakenly believe that two rectangles with the same perimeter have the same area and vice versa (Examples 1 and 2).

Example 1

The teacher asks students if two-dimensional shapes with equal areas also have the same perimeters. A student says, “I think that if two-dimensional shapes have equal areas, they also have the same perimeters.” The teacher asks the other students if they think this is true or false. The teacher forms teams of two and suggests that they test the conjecture. To do this, the teacher suggests the following procedure. The teacher gives students a set of tangrams, sheets of graph paper, string and scissors. The teacher asks them to use all the pieces of the tangrams to build three shapes of their choice.

In each case, the student must:

• trace the outline of the shape on the sheet of graph paper;
• determine the number of square units that cover the area;
• trace the outline of the shape with string and cut it to the right length;
• stick the string on the board next to the previous string;
• record the perimeter and area measurements in the table below.

During the math conversation, teachers ask students to observe the results and see that:

• all shapes have the same area since they are assembled with the same pieces;
• not all shapes have the same perimeter.

Students can then conclude that the conjecture is false, namely, that while two-dimensional shapes have the same area, they do not necessarily have the same perimeter.

Example 2

The teacher asks students if two-dimensional shapes that have the same perimeter have the same area. A student says, “I think that even though two-dimensional shapes have the same perimeter, they don't necessarily have the same area”. The teacher asks the other students if they think this is true or false. The teacher forms teams of two and suggests that they test the conjecture. To do this, the teacher suggests the following procedure.

Teachers ask students to draw as many different rectangles with a perimeter of 16 units as possible on a sheet of graph paper.

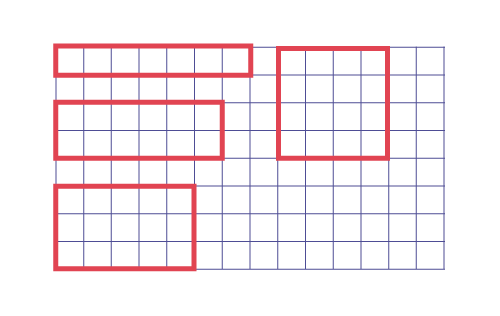Image A number of different rectangles in different sizes are drawn on a gridded sheet. The rectangles all have a perimeter of 16 units.

For each rectangle, the student must:

• trace the outline of the rectangle on the sheet of graph paper;
• determine the perimeter and area of the shape;
• record perimeter and area measurements in their math journal.

During the math conversation, teachers ask students to observe the results and see that:

• all shapes have a perimeter of 16 cm;
• not all shapes have the same area.

Students can then conclude that the conjecture is true, namely, that while two-dimensional shapes have the same perimeter, they do not necessarily have the same area.

Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3^e année, Mesure, p. 68-73.

Knowledge: Standard Units (Square Centimetres and Squares Metres)

---

The square centimetre and the square metre are standard units of area in the metric system.

• A square with dimensions of \(\ 1 \mathord{cm} \times 1 \mathord{cm}\) has an area of one square centimetre (1 cm²).
• A square with dimensions of \(\ 1 \mathord{m} \times 1 \mathord{m}\) has an area of one square metre (1 m²).
• Square centimetres and square metres are amounts of area. Although their definitions are based on squares, they can come in any shape.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.