E1.1 Sort, construct, and identify cubes, prisms, pyramids, cylinders, and cones by comparing their faces, edges, vertices, and angles.
Activity 1: Technological Activities (Constructing Geometric Shapes)
Instructions
Construct various geometric shapes on the computer using the draw feature of a word processer.
Note: This kind of activity allows students to identify and compare three-dimensional objects according to the number of edges, vertices and faces, the type of faces and the congruence of faces or two-dimensional shapes, the number of vertices, sides, length of sides...
Teacher Moves
Ask questions such as:
- Which three-dimensional object has only triangular faces? Are they congruent?
- Which three-dimensional objects have a square base?
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 49.
Activity 2: I Fill in the Table (Recognizing, Naming, Comparing and Sorting Three-Dimensional Objects)
Present the following table to students.
Ask students to put a check mark in the second column when the property also applies to the square-based prism.
|
Cube Description |
Square-Based Prism |
|
6 sides |
|
|
8 vertices |
|
|
12 edges |
|
|
6 congruent faces |
Teacher Moves
Ask questions such as:
- What is the difference between a cube and a square-based prism?
- How are the two three-dimensional objects similar?
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 50-51.
Activity 3: Mystery Three-Dimensional Object (Recognizing Three-Dimensional Objects)
Material
- three-dimensional objects
Instructions
Place the following three-dimensional objects on a table for students to see: a cube, a square-based prism, a rectangle-based prism, a triangle-based pyramid, a sphere, a cone and a cylinder.
Invite a student to choose, without pointing or naming, a mystery three-dimensional object and to inform you discreetly of their choice.
Ask the other students to try and discover the mystery three-dimensional object by asking yes/no questions. Clarify that the questions asked must be about the properties of the three-dimensional objects, including the number of faces, edges, vertices, and angle. The student who has chosen the three-dimensional object answers the questions.
The student who finds the mystery three-dimensional object chooses one in turn and has the others guess their choice.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 78.
Activity 4: Guessing Game
Instructions
Here is my train composed of three cars:
- my first car has six congruent sides;
- my last car has only one identifiable apex.
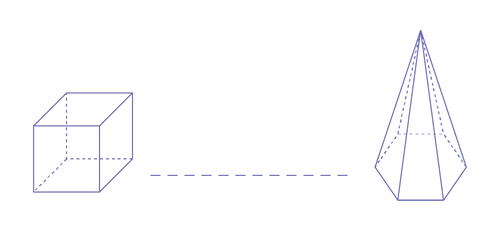
Find the middle car by its name and by the property that connects it to the other two. Several answers are possible.
Example: My middle car is the rectangle-based prism.
- The prism with a rectangular base resembles the cube, because it also has eight vertices.
- The rectangle-based prism resembles the hexagon-based pyramid in that it also has 12 edges.
Ask students to make up their own riddles and ask them in class.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 127-128.
Activity 5: Weird Three-Dimensional Objects
Instructions
Have students make cubes, prisms, and spheres out of play dough.
Remove a piece of the three-dimensional objects.
Ask students to name and describe the new three-dimensional objects.
If the new three-dimensional object does not resemble any known three-dimensional object, create an odd name.
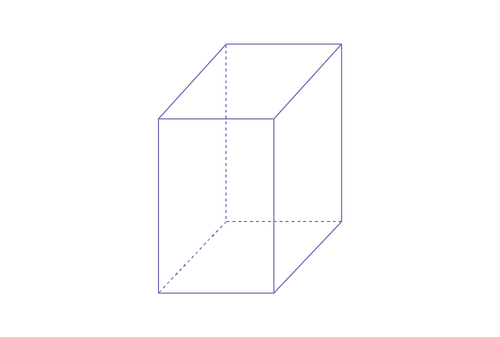
Example 1
Slice off the corner of a cube, as shown in the illustration below.

We choose to call the new three-dimensional object a cubi, an almostcube, a cubo...
It has seven faces, twelve edges and seven vertices. Three faces are square and congruent. The other four faces are triangular. One face is larger than the other three.
Example 2
Slice the corner of a rectangle-based prism, as in the illustration below.
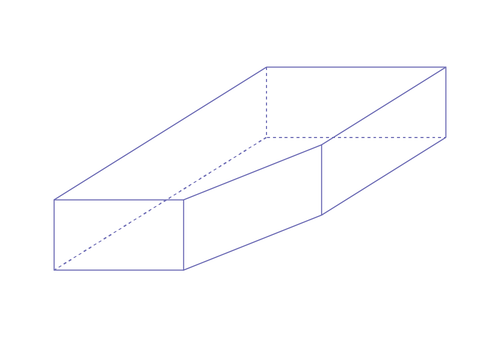
We choose to call the new three-dimensional object a prismo, a pentaprism...
It has seven faces, fifteen edges and ten vertices. It has five rectangular faces. The other two faces are pentagon-shaped and congruent.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 128-129.
