E1.2 Plot and read coordinates in the first quadrant of a Cartesian plane, and describe the translations that move a point from one coordinate to another.
Skill: Locating Coordinates in the First Quadrant of a Cartesian Plane
The location of a coordinate is written as an ordered pair (x, y) with x representing the number of steps, right or left, that the point is from the origin, and with y representing the number of steps, up or down, that the point is from the origin.
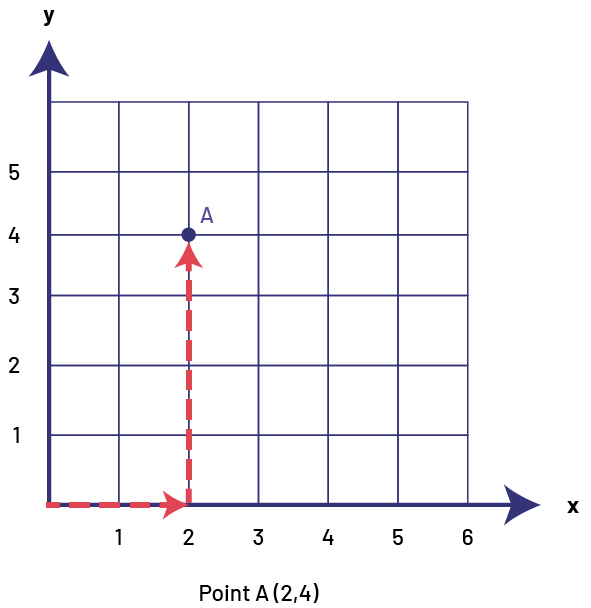image A grid with five columns and five rows. The columns are numbered on the horizontal axis, "x", and the rows on the vertical axis, "y". There is a point "a" at the intersection "y" four and "x" two, and "y" one and "x" four. The second "a" is marked by an apostrophe.
The importance of the order in which numbers are written in an ordered pair should be emphasized to students by asking them to locate points A (2, 4) and B (4, 2); students will quickly realize that these points describe different locations.
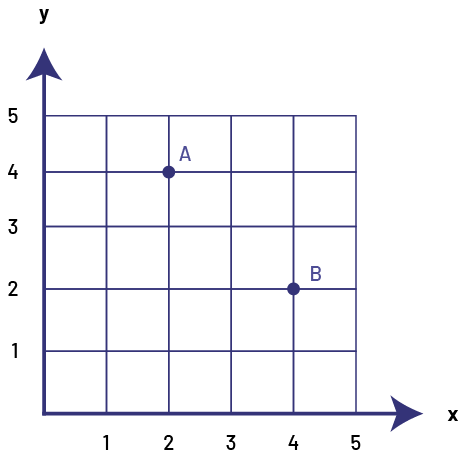image A grid with five columns and five rows. The columns are numbered on the horizontal axis, "x", and the rows on the vertical axis, "y". There is a point "a" at the intersection of "y" four and "x" two, and a point "b" at the intersection of "y" two and "x" four.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25.
Skill: Reading Coordinates in the First Quadrant of a Cartesian Plane
To read coordinates of a point in the first quadrant of a Cartesian plane, begin by following the vertical line on which it is located to the x-axis. This is the x coordinate. And then do the same by following the horizontal line to the y axis. The number that corresponds to the horizontal position first and the number that corresponds to the vertical position second. Students need to understand that the Cartesian coordinate described by an ordered pair such as (2, 4), defines one of the points of intersection of the lines, and not one of the squares formed by the lines.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25.
Skill: Describing Movements from One Coordinate to Another Using Translations
On a Cartesian plane, movements of points to the right, left, up and down are translations.
To describe a horizontal or vertical translation, students use words, letters, or symbols. For example, a translation of three units to the right can be symbolically represented by 3R or 3→. To describe an oblique translation, both the horizontal and vertical movements must be indicated. For example, a translation of three units to the right and two units down is symbolically represented by (3R, and 2D) or (3→ and, 2↓). The order of the symbols does not matter; however, it is best to get students used to always describing the translation by indicating the horizontal movement first and then the vertical movement.
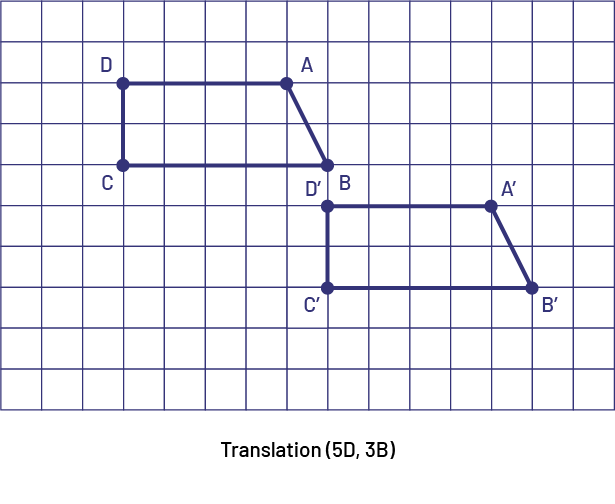image Grid with 15 columns and 10 rows. There are two oblique quadrilaterals on the grid. Points "a", "b", "c", and "d" are identified on the first quadrilateral. The points "a" apostrophe, "b" apostrophe, "c" apostrophe, and "d" apostrophe are identified on the second quadrilateral.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 28.
Knowledge: Cartesian Plane
The Cartesian plane is a coordinate system for precisely locating the position of a point in a plane.
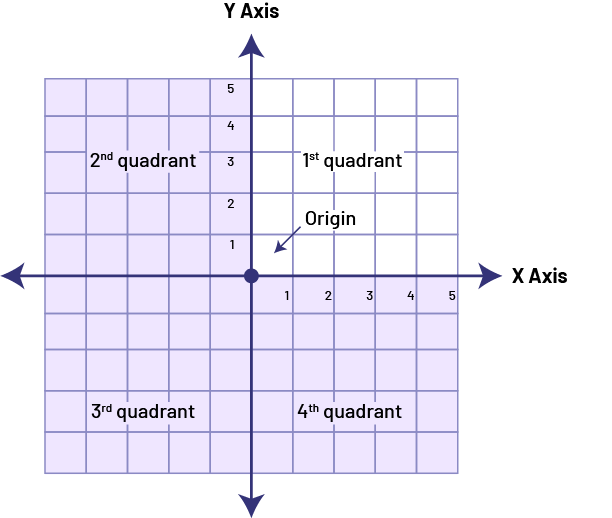image A Cartesian plane consisting of four quadrants, starting from the upper right corner and going counterclockwise. In the first quadrant, five rows are numbered on the horizontal "x" axis and five columns on the vertical "y" axis. The point of origin at the intersection of two axes is marked by a dot.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: A Coordinate
A coordinate is a point on a Cartesian plane and is described by a ordered pair. For example, the coordinates (3,5) describe a location found by moving 3 units to the right and 5 units up from the origin (0, 0). The coordinates are written in parentheses and are separated by a comma as follows: point A (2, 4). By convention, the first number, called the abscissa, indicates the horizontal position of the point with respect to the origin, and the second, called the ordinate, indicates its vertical position. Note that Grade 4 students are not required to use the vocabulary abscissa and ordinate.
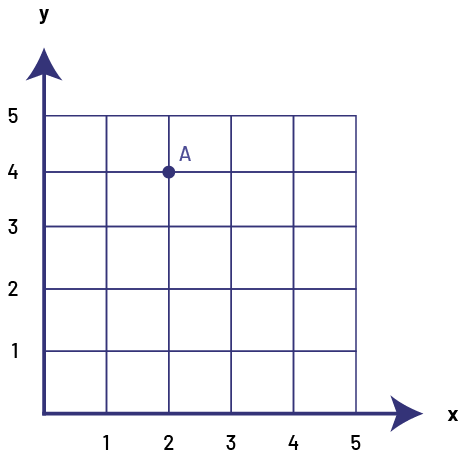image A grid with five rows and five columns. The rows are numbered on the horizontal axis, "x" and on the vertical axis, "y". There is a point "a" located at the intersection of "x" two and "y" four, and a point "b" located at the intersection of "x" four and "y" two.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25.
Knowledge: The First Quadrant of a Cartesian Plane
The x and y axes divide the Cartesian plane into four regions called quadrants. Grade 4 students use only the quadrant at the top right of the Cartesian plane, the first quadrant.
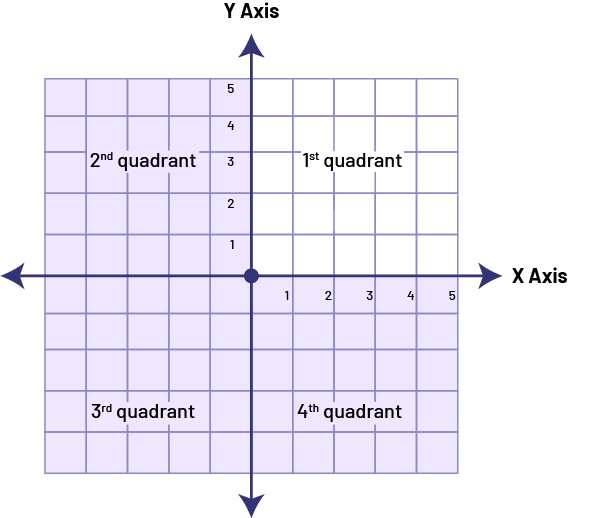
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: Translating a Coordinate
Translating a coordinate is changing the location of a point in a Cartesian plane to a different horizontal or vertical position.
Example
The point (2, 4) is moved 2 units to the right (2R) and 3 units down (3D) and its new coordinates are (4, 1).
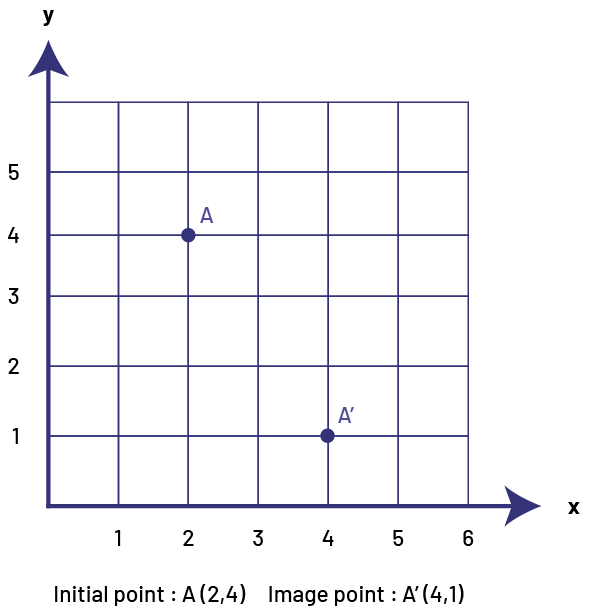image A grid with five rows and five columns. The rows are numbered on the horizontal axis, "x" and on the vertical axis, "y". There is a point "a" at the intersection of "x" two and "y" four, and "x" four and "y" one. The second "a" is marked by an apostrophe.
Knowledge: Translation
The translation is defined by its size and direction (represented symbolically by coordinates or by an arrow). It represents a linear, horizontal, vertical, or diagonal movement in which the initial shape and the image are congruent. The distance between each point on the initial shape and the corresponding point on the image is constant. The orientation of the image is the same as the orientation of the initial shape.
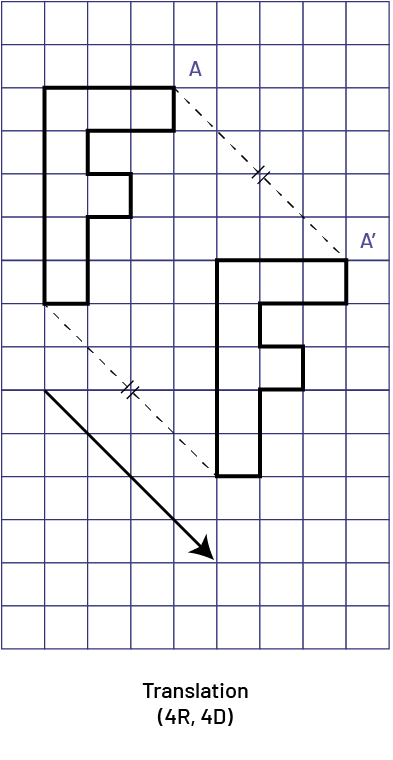image A grid of nine columns and 15 rows. There are two letters "f" placed obliquely on the grid. The "a" points of the two "f" are connected by a line. Another parallel line connects the bottom of the "f". There is a diagonal arrow pointing to the right, downwards.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 36-37.
Knowledge: Horizontal Axis
Two perpendicular axes are used to define the Cartesian plane. The horizontal axis is designated by an x and is called the x-axis.
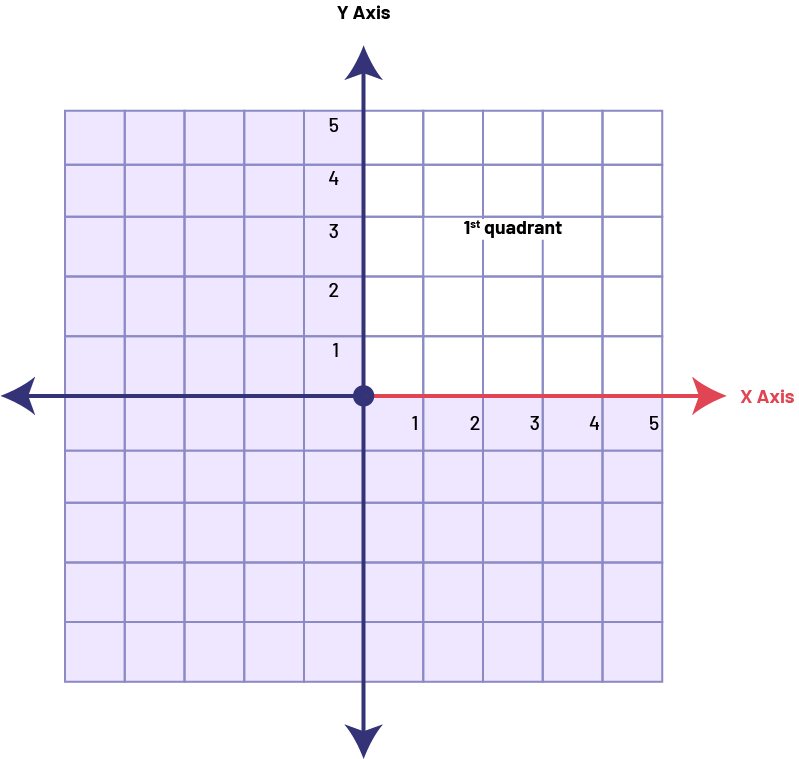
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: Vertical Axis
Two perpendicular axes are used to define the Cartesian plane. The vertical axis is called the y-axis.
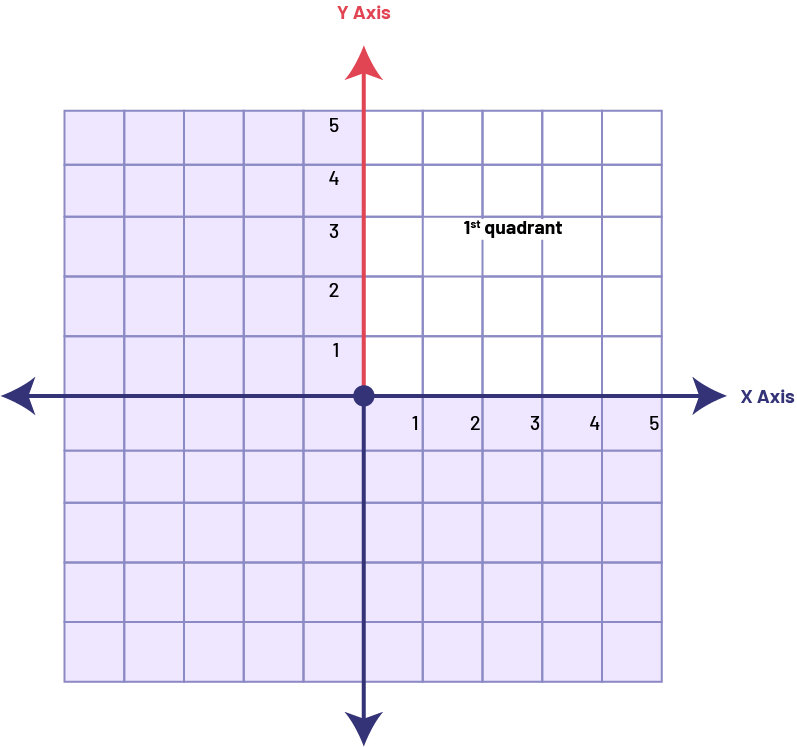
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: The Origin
The point (0,0) where the horizontal and vertical axes meet, and serves as a reference point, is the origin.
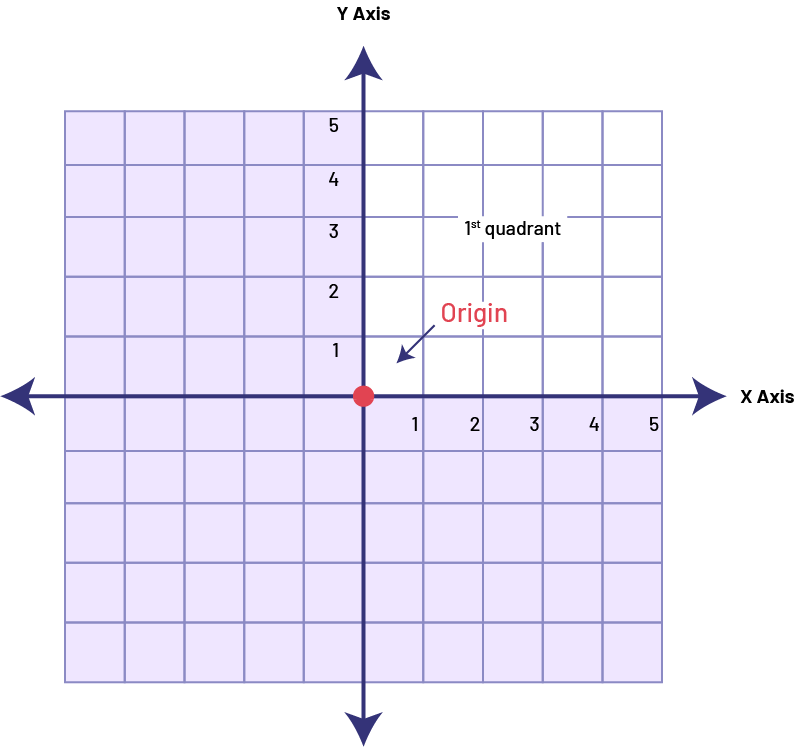image A Cartesian plane consisting of four quadrants. Only the first quadrant is identified. In the latter, five rows are numbered on the horizontal "x" axis and five columns on the vertical "y" axis. The point of origin, at the intersection of the "x" and "y" axes, is identified by a red dot.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.