E1.3 Describe and perform translations and reflections on a grid, and predict the results of these transformations.
Activity 1: Reflection on a Geoboard
Instructions
Provide each student with a geoboard and rubber bands.
Present a virtual geoboard on the whiteboard and build an irregular pentagon in front of the students.
Build a vertical line of reflection with another rubber band.
Tell students that the pentagon (initial shape) will be reflected in a vertical line.
Build the image of the initial shape on the geoboard.
Teacher Moves
Be sure to reflect left and right using a vertical line of reflection, and down and up using a horizontal line of reflection.
Have them check the congruence of the initial shape and the image.
Point out that each point on the initial shape is equidistant from the corresponding point on the image and that the image is the reverse of the initial shape.
Source: translated from Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 69-70.
Activity 2: Complete the Drawing (Symmetry)
Instructions
Using a geoboard or dot paper, ask the students to reproduce this drawing.
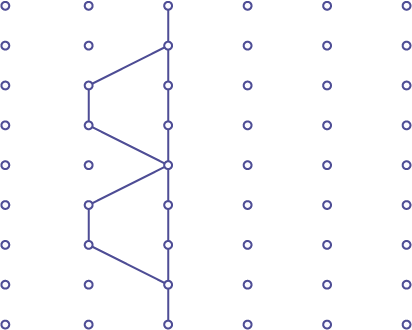
Ask a student to complete the drawing using a Mira.
Ask the following questions:
- Why is this drawing a symmetrical two-dimensional shape?
- How many lines of symmetry does the completed two-dimensional shape have?
Distribute additional drawings for students to complete.
Propose some drawings with a horizontal line of symmetry.
Example
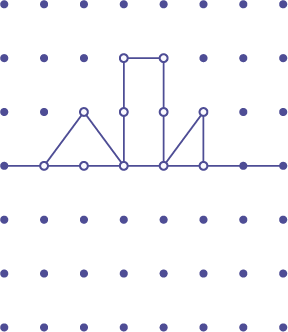Allow students time to complete the drawings.
Note: This activity can be done in pairs. While one student holds the Mira firmly in place, the other student traces. The roles are then reversed.
Teacher Moves
Discuss by asking questions about the lines of symmetry.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Géométrie et sens de l'espace, p. 51-52.