E2.1 Use appropriate metric units to estimate and measure length, area, mass, and capacity.
Skill: Estimating Measurements
In the junior grades, students must learn to use a variety of strategies to estimate in increasingly complex situations using both non-standard and standard units. It is important, therefore, that the teachers plan supports and direct instruction focused on specific estimation strategies. Van de Walle and Lovin (2008) suggest teaching four estimation strategies. These strategies are presented in the following table.
|
Strategy |
Example |
|
Develop and Use Benchmarks for Important Units of Measurement Students who have built up a repertoire of benchmarks and use them regularly are more successful and comfortable estimating. Estimating the measurement of the attribute is done by comparing it with a benchmark. |
To estimate the measurement of a given angle, the right angle and the flat angle can be used as benchmarks. By mentally superimposing the image of these angles on the given angle, students can conclude that the measurement is much closer to 90o than 180o. The measurement of the given angle is about 100o. 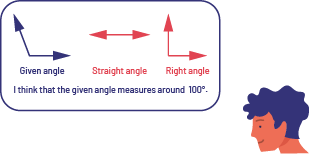 image In a rounded rectangle, there are three angles: a given angle which is formed by a short vertical line and a short diagonal line to the left, a flat angle, and a right angle. At the bottom of the rectangle is written: I believe that the given angle measures about one hundred degrees. Outside the rectangle, there is a character. image In a rounded rectangle, there are three angles: a given angle which is formed by a short vertical line and a short diagonal line to the left, a flat angle, and a right angle. At the bottom of the rectangle is written: I believe that the given angle measures about one hundred degrees. Outside the rectangle, there is a character. |
|
Break Down the Object Into Parts In some contexts, it is easier to estimate the measure of an attribute for an object by first estimating the size of smaller, easily identifiable parts of that object. The estimate will be the sum of the size of each of the parts. |
To estimate the height of a 12-story building, students can first estimate that the height of the first floor is about 3 m. Assuming that all floors are the same height, they can then estimate that the building is about 36 m high.  |
|
Use of Subdivisions If the object to be measured has no elements that suggest a way to break it down into parts, it can first be divided mentally or concretely into halves, and then one of these halves can be divided again into halves and the process repeated until a section is obtained whose measurement can be estimated. |
To estimate the area of a large blanket, students can fold it in half repeatedly to create a relatively small blanket surface. They can then estimate the area of this surface and multiply the result by the number of such surfaces created.  Note: Students can make connections to the Algebra strand and explore the relationship between the number of folds and the number of surfaces created by, for example, folding a piece of paper and recording in a chart the number of identical surfaces obtained after each fold. They could then point out that each time a fold is added, the number of surfaces is doubled. 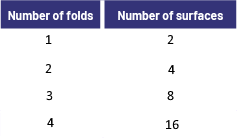 |
|
Iterate Concretely or Mentally Iteration refers to the act of placing, repeatedly and in an orderly fashion, the same unit of measurement in order to determine the measure of some attribute. The number of times the unit of measurement is placed then corresponds to the measure of the attribute. |
To estimate the area of a box using a sticky note as a unit, students can try to visualize the number of times a sticky note can be placed on the box without overlapping or leaving gaps.  |
When students engage in estimation activities on a regular basis, they realize that there is no single effective estimation strategy. Teachers should provide students with frequent estimation activities related to measurable attributes. These activities are most effective when students share, discuss, justify and explain how they arrived at their results. Explanations and justifications of students' estimates allow teachers to learn about and even assess students' understanding of measurement concepts and procedures.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 18-19.
Skill: Using Appropriate Metric Units of Measurement
The act of measuring involves a series of reflections, decisions and actions that lead to obtaining and communicating an accurate and appropriate measurement for a given context. This involves a series of steps that are the same for all the attributes studied in the Junior Division: length, area, angle, capacity, mass and time. Although the number and identification of these steps vary somewhat, depending on the researcher, they can generally be articulated sequentially as follows:
- determine the attribute to be measured;
- choose the unit;
- determine the measurement;
- communicate the result.
Determine the Attribute to Be Measured
In any problem that involves the act of measuring, the first step is to determine the attribute of the object that is to be measured. Is it, for example, length, area, capacity, or mass? To be able to determine the attribute to be measured in a given situation, students must have a clear understanding of the meaning of each attribute. Teachers should provide a variety of learning situations that encourage students to determine measurable attributes of an object and to choose the one that will allow them to solve the problem.
Choose the Unit of Measurement
The second step in the act of measuring is to select an appropriate non-standard or standard unit to measure an attribute of the object. To do this, it is important to choose a unit that reflects the attribute to be measured and is appropriate for the situation. In addition, it is generally best to use a single unit. Finally, it is also important that the choice of unit takes into account the degree of precision of the measurement sought (for example, a mass measurement to the nearest kilogram or gram).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 83-86.
However, precision is not always necessary and may be a waste of time. It could also complicate the measurement.
When it comes to choosing the appropriate unit, the same metric prefixes apply to all attributes (except time) and designate the relationships between the units. A unit just to the left of a particular unit in the chart is 10 times greater, and the unit just to its right is 10 times less.
| Metric prefix | kilo- | hecto- | deca- | No prefix | deci- | centi- | milli- |
|---|---|---|---|---|---|---|---|
| Unit value | 1000 units | 100 units | 10 units | 1 unit | \(\frac{1}{10}\) unit | \(\frac{1}{100}\) unit | \(\frac{1}{1000}\) unit |
| Place value | thousand | hundred | ten | one | one tenth | one hundredth | one thousandth |
Source: The Ontario Curriculum,Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.
Skill: Measuring Length, Area, Mass and Capacity
Determine the Measurement
The third step in the act of measuring is to determine the measurement of an attribute of the object, that is, to give an order of magnitude to the attribute by quantifying it in terms of a unit.
Steps in the Act of Measuring
- determine the attribute to be measured;
- choose the unit of measurement;
- determine the measurement;
- communicate the result.
Using a Measuring Tool
Many measuring tools (for example, ruler, thermometer, scale) have been designed to determine the measurement of various attributes in terms of standard units. Although this strategy provides a quick measurement, it requires the user to have a good sense of measurement and a good ability to abstract. To help students understand the importance of these measuring tools and how to use them correctly, teachers can offer to build one.
In the junior grades, it is important that students learn to use some of the common measuring tools such as those listed in the table below, taking into account the degree of precision sought and the importance of accuracy of measurement.
|
Attribute |
Instruments |
|
Length |
|
|
Mass |
|
|
Capacity |
|
In any situation involving measurement, the degree of accuracy sought determines the size of the unit that should be used. It is defined by the need or intent of the measurement. In some situations, for example, it may be sufficient to know that the height of a door frame is about 2 m. However, this measurement, given to the nearest metre, is still approximate and has a low degree of accuracy. It is very likely that the height of the frame is actually a little less or a little more than 2 m. If a door is to be made to fit into the frame, it is necessary to obtain a measurement with a higher degree of accuracy. In this case, smaller units must be used, corresponding to fractions of a metre (for example, centimetres). We could then determine that the height of the door frame is, to the nearest centimetre (for example, 213 cm).
Students should recognize the importance of choosing a unit that matches the degree of precision that the measurement situation explicitly or implicitly requires.
The accuracy of the measurement depends on the way the measuring tool is used. If the tool is not used properly, the measurement obtained will not be accurate; it will be greater or less than the quantity being measured. To help students understand the proper use of a given measuring tool, teachers should first model its use.
Some details about how to use certain measuring tools are presented below.
To use a ruler correctly, you must:
- align one end of the object with the zero or the beginning of the scale lines;
- make sure that the line of sight of the other end of the object is at a 90° angle to the ruler (see Parallax Error in the illustration below);
- count, on the ruler, the units that go from one end of the object to the other.
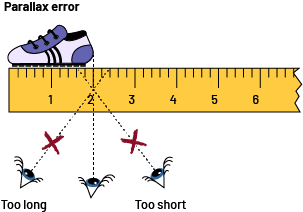 image A ruler measuring six centimeters. On top of it, there is a shoe, above that, it is labeled: parallax error. Under the ruler there are three eyes, that are linked to the ruler by three different dotted lines. Above the first eye, there is an "x" and below it is marked: too long. Above the third eye, there is an "x" and below it is marked: too short.
image A ruler measuring six centimeters. On top of it, there is a shoe, above that, it is labeled: parallax error. Under the ruler there are three eyes, that are linked to the ruler by three different dotted lines. Above the first eye, there is an "x" and below it is marked: too long. Above the third eye, there is an "x" and below it is marked: too short.
To properly use a two-pan balance, you must:
- place the balance on a flat horizontal surface;
- make sure the scale and the pans are in balance before placing the object to be measured on one of the pans;
- place the object to be measured on one of the pans and, in the other tray, put one of the chosen mass units (for example, a mass of 1 g);
- add mass units until the two pans are in balance again;
- count the units of mass used.

To correctly use the triple beam balance, you must:
- place the balance on a flat horizontal surface;
- make sure the arrow points to zero before placing the object to be measured on the platter;
- place the object to be measured in the center of the tray;
- move the sliding weights, one at a time, always starting with the largest weight (for example, the 100 g weight, then the 10 g weight, and finally the 1 g weight) and always making sure to place the weights in one of the notches;
- make sure the arrow is always pointing above zero before moving a weight to the next notch;
- if the arrow points below zero, move the weight back one notch and move the next (smaller) weight;
- proceed in this way until the arrow points to zero;
- read the mass of the object according to the graduations where each of the three masses are inserted.

To properly use a graduated cylinder, you must:
- make sure to place the graduated cylinder on a flat horizontal surface;
- slowly pour the liquid in, taking care not to create air bubbles;
- make sure you are positioned to read the volume of liquid with the meniscus in mind;
- read the volume of liquid according to the scale on the wall of the graduated cylinder (for example 100 ml).
The curvature of the surface of a liquid in a container is called a meniscus. In a graduated cylinder, a liquid such as water sticks to the wall, and the meniscus takes on a concave shape. The reading of the volume of liquid must be taken at the lowest point of the meniscus.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 89-98.
Communicate the Result
The fourth and final step in the act of measuring is to communicate the result. Once students have determined the measurement of an attribute of the object, teachers should encourage them to demonstrate their understanding of the resulting measurement by clearly communicating their result using appropriate mathematical vocabulary and units.
Steps in the Act of Measuring
- determine the attribute to be measured;
- choose the unit;
- determine the measurement;
- communicate the result.
After determining, for example, that the height of the column of liquid (mercury or alcohol) in the classroom thermometer is 20, some students may be inclined to simply say, "It is 20." Teachers should encourage them to always express their result by stating the attribute and object being measured, as well as the unit used. They can also prompt students to show their understanding of this result by comparing it to another measurement or situation (for example, "It's a comfortable temperature; it's not as hot as outside.") The table below provides various examples of clear communication related to the different measurement attributes under consideration.
|
Measured Attribute |
Selected Unit of Measurement |
Quantity |
Communication of the Result |
|
Length of a notebook |
centimetre |
25 |
The length of the notebook is 25 cm. |
|
Mass of a bucket filled with water |
kilogram |
8 |
The bucket filled with water has a mass of 8 kg. |
|
Area of the surface of a box |
square centimetre |
168 |
The area of the surface of the box is equal to 168 cm2. |
|
Capacity of a coffee cup |
millilitre |
300 |
The coffee cup has a capacity of 300 ml. |
Teachers should ensure that students can read the symbols correctly when communicating their results orally. Students should say, for example:
- "The length of the notebook is 25 centimetres." not "The length of the notebook is 25 c-m.";
- "The area of the surface of the box is equal to 168 square centimetres." not "The area of the surface of the box is equal to 168 c-m to the exponent 2."
Teachers should also ensure that students know how to correctly write the symbols representing the various units of measurement, according to established conventions. In order to do this, teachers should use wording that clearly refers to the attribute during mathematical exchanges. For example, Which apple has the most mass?
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 102-105.
Knowledge: Benchmarks Associated with Length
Since benchmarks are essentially mental images, their development is intimately associated with one's ability to visualize. Students generally do not have too much difficulty developing appropriate benchmarks for the length; for example, the mental image of one side of a small connecting cube can represent 1 cm, the mental image of the width of a door can represent 1 m, or the mental image of the length of 2.5 laps of a track can represent 1 km.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 14.
Knowledge: Benchmarks Associated with Area
Since benchmarks are essentially mental images, their development is intimately associated with the ability to visualize. Students generally do not have too much difficulty developing appropriate benchmarks for the area attribute; for example, the mental image of the area of one face of a small interlocking cube to represent 1 cm2.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 14.
Knowledge: Benchmarks Associated with Mass
According to Lindsay and Scott (Estimating Eggs: An Activity to Help to Promote the Exploration of Mass Estimation Concepts, 2005, p. 3), it is very difficult to develop benchmarks for mass because of the difference between visual and tactile acuity. This is because sight can generally recognize very small differences in length between two objects. However, it is rather difficult when weighing two objects to discern a small difference in mass (for example, a difference of less than 100 g). Teachers should provide students with multiple opportunities to weigh various objects to help them develop benchmarks for mass (for example, a bag of sugar has a mass of 2 kg or 2000 g).
In addition, the volume of an object sometimes affects the perception of its mass. For example, students sometimes feel that a large-volume object necessarily has a greater mass than a small-volume object. Similarly, when students look at two objects of the same volume, some feel that they necessarily have the same mass. They need only think of two boxes of the same size, one filled with books and the other filled with feather pillows, to understand that this is not the case.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 15.
Knowledge: Benchmarks Associated with Capacity
Capacity refers to the amount of a substance that a package can hold. It is sometimes difficult for students to develop benchmarks for this attribute, since the capacity of a package can be expressed in grams (for example, the capacity of a box of cereal), milliliters or liters (for example, the capacity of a juice container), or cubic centimeters (for example, the capacity of a packing box). It can also be expressed in terms of the number of identical objects that a package can hold (for example, a cylindrical container that has a capacity of three tennis balls). In addition, since liquids take on the shape of the container in which they are placed, it is difficult for students to form a mental image of a 1L or 1 mL capacity without considering the container. Teachers can encourage students to use a variety of items found in the home to develop benchmarks for the capacity attribute (for example, a 1L bag of milk, a 500 mL bottle of water, a 250 g box of cookies).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 16.
Knowledge: Length Attribute
Length is a measure in a one-dimensional space.
A length can refer to:
- the size of a segment, in other words the distance between two points;
- the distance between two parallel lines or two parallel planes;
- a perimeter;
- a height, a depth, a thickness, a width, a size.
Note: For some students, these different terms associated with length may be confusing.
Examples
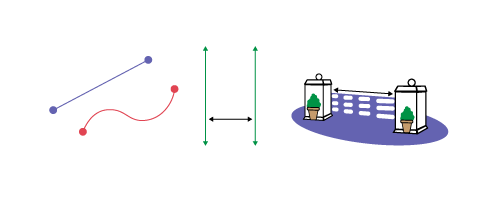 image There are three symbols. The first is composed of a straight line and a wavy line. The second is composed of a set of vertical lines and a horizontal line that identifies the distance between the lines. The third is a fence with a height of three boards. There is a line that identifies the length of the planks.
image There are three symbols. The first is composed of a straight line and a wavy line. The second is composed of a set of vertical lines and a horizontal line that identifies the distance between the lines. The third is a fence with a height of three boards. There is a line that identifies the length of the planks.
The perimeter is the length of the contour of a two-dimensional shape or of any three-dimensional object.

The length of a book becomes its height when stored upright on a shelf, just as its thickness becomes its width.
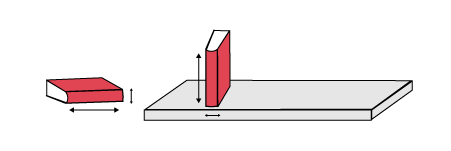
Source: translated from Fiche de la 4e à la 6e année, Attribut longueur.
Knowledge: Area
Area refers to a measure of the space inside a two-dimensional space. The size of a piece of land and the area of a country are examples of area.
 image There are two illustrations. In the first one is a map of Canada. On top of it is marked: the area of Canada is nine million 984 thousand 670 square kilometers. In the second picture there is a construction site and a fence under a sunny sky. Under the image is labeled: Mr. and Mrs. Sanchez farm has an area of 450 thousand square meters.
image There are two illustrations. In the first one is a map of Canada. On top of it is marked: the area of Canada is nine million 984 thousand 670 square kilometers. In the second picture there is a construction site and a fence under a sunny sky. Under the image is labeled: Mr. and Mrs. Sanchez farm has an area of 450 thousand square meters.
Source: translated from Fiche de la 4e à la 6e année, Attribut aire.
Knowledge: Mass
Mass refers to the amount of matter in an object. Only the kind of matter that constitutes an object influences its mass. Thus, the mass of an object does not vary depending on where it is located on Earth (or in space).
The mass of an object is determined using, for example, a triple-beam balance or a two-pan balance.
Note: Mass and weight should not be confused. The weight of an object is the force exerted by a celestial body on that object. It is determined with a dynamometer and is expressed in newtons (N). The weight of an object varies according to its mass and where it is located on Earth (or in space).
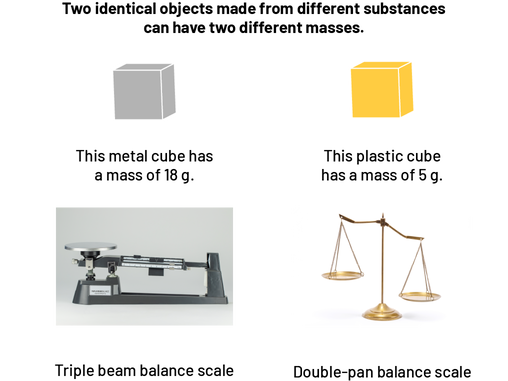 image There are four pictures, on top of is labeled: two objects of the same size that are made of a different material can have a different masses. The first picture is of a cube of matter, the second of a cube of plastic, the third of a triple beam balance, and the fourth of a double pan balance. Under the first cube is written: this cube of matter has a mass of 18 grams. Under the second cube is labeled: this cube of plastic has a mass of five grams. Under the first scale is written: triple beam scale. Under the second scale is labeled: scale with double plates.
image There are four pictures, on top of is labeled: two objects of the same size that are made of a different material can have a different masses. The first picture is of a cube of matter, the second of a cube of plastic, the third of a triple beam balance, and the fourth of a double pan balance. Under the first cube is written: this cube of matter has a mass of 18 grams. Under the second cube is labeled: this cube of plastic has a mass of five grams. Under the first scale is written: triple beam scale. Under the second scale is labeled: scale with double plates.
Source: translated from Fiche de la 4e à la 6e année, Attribut masse.
Knowledge: Capacity
The capacity of a container is the maximum amount that it can hold. When the given substance completely fills the container, the capacity is equal to the interior volume of the container.
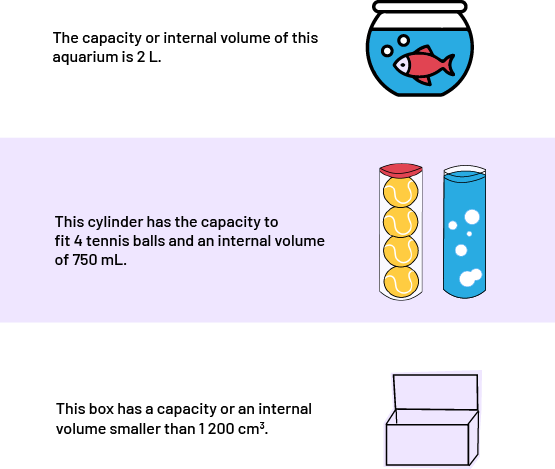 image Three pictures: A fish in an fish bowl; a cylinder containing three tennis balls and a cylinder filled with water; and a cardboard box. Next to the picture of the fish bowl is labeled: the capacity or volume of this fish bowl is two liters. Next to the picture of the cylinders is labeled: this cylinder has a capacity of three tennis balls and an interior volume of 750 milliliters. Next to the picture of the cardboard box is labeled: This box has a capacity or interior volume of one thousand 200 cubic centimeters.
image Three pictures: A fish in an fish bowl; a cylinder containing three tennis balls and a cylinder filled with water; and a cardboard box. Next to the picture of the fish bowl is labeled: the capacity or volume of this fish bowl is two liters. Next to the picture of the cylinders is labeled: this cylinder has a capacity of three tennis balls and an interior volume of 750 milliliters. Next to the picture of the cardboard box is labeled: This box has a capacity or interior volume of one thousand 200 cubic centimeters.
Source: translated from Fiche de la 4e à la 6e année, Attribut capacité.
