E2.6 Show that two-dimensional shapes with the same area can have different perimeters, and solve related problems.
Skill: Demonstrating That Two-Dimensional Shapes with the Same Area Can Have Different Perimeters
Relationships between Attributes
Exploring the relationships between attributes allows students to develop a better understanding of the common formulas used to determine the area of certain two-dimensional shapes or the volume of certain three-dimensional objects, and to apply them knowledgeably in various problem-solving situations.
Relationship between Length and Area
Teachers should introduce students to measurement activities that allow them to relate the dimensions (base and height) of certain two-dimensional shapes (rectangle, parallelogram, and triangle) to their area. Students should build the concepts of "height" and "base" through activities that help them understand that any of the sides of a shape can be the base and that for every base there is a corresponding "height".
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 70.
Teachers can also provide activities that allow students to explore situations in which there is no relationship between the attributes length and area. This type of activity helps students better understand the importance of checking a conjecture before concluding that it is true.
Example 1
Teachers ask students if they think there is a relationship between the perimeter of two two-dimensional shapes that have the same area. A student says, "I think that if two two-dimensional shapes have the same area, they also have the same perimeter." The teacher asks the other students if they think this is true or if they think it is false. The teacher then groups the students into pairs and suggests that they test the conjecture.
To do this, teachers will suggest the following procedures for students:
- draw two identical squares;
- determine the area and perimeter of the squares;
- draw a diagonal in one of the squares and cut the square to obtain two triangles;
- form new two-dimensional shape using these two triangles and determine the perimeter;
- use the results to determine if the conjecture is true or false.

The pictures below show two shapes that could be formed using triangles. Using these shapes, students can see that although the area of each shape is equal to the area of the original square, the perimeter measurements are different. They can then conclude that the conjecture is wrong and that if two two-dimensional shapes have the same area, they do not necessarily have the same perimeter.

Example 2
Teachers ask students if they think there is a relationship between the area of two two-dimensional shapes that have the same perimeter. A student says, "I think that even though two two-dimensional shapes have the same perimeter, they don't necessarily have the same area." The teacher asks the other students if they think this is true or if they think it is false. The teacher then groups the students into pairs and suggests that they test the assumption.
To do this, the teacher suggests the following procedure:
- draw on graph paper various rectangles that have a perimeter of 16 cm;
- determine the area of each of the rectangles;
- use the results to indicate whether the conjecture is true or false.
The illustration below shows some rectangles that could be drawn. Using these rectangles, students can see that although the rectangles have the same perimeter (16 cm), they do not have the same area. They are then able to conclude that the conjecture is true that if two two-dimensional shapes have the same perimeter, they do not necessarily have the same area.
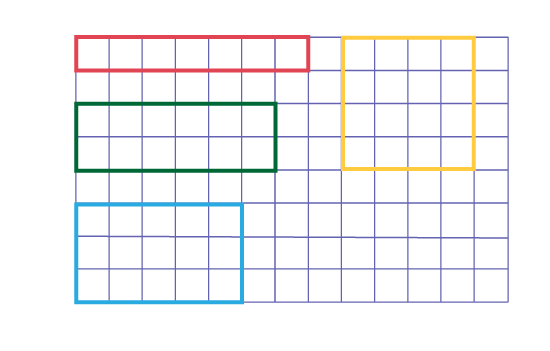
Note: The teacher can prompt students to think further and see that the rectangle with the largest area for a given perimeter is the square.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 77-79.
