La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

Learning Situation: The Pentacube Box

Total duration: approximately 90 minutes

Summary

In this learning situation, students create a game that involves inserting three-dimensional objects (flat pentacubes) into openings cut in a shoebox.

Overall Expectation

Specific Expectations

E1.Geometric and Spatial Reasoning Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them.

E1.1 Create lists of the geometric properties of various types of quadrilaterals, including the properties of the diagonals, rotational symmetry, and line symmetry.

E1.4 Describe and perform combinations of translations, reflections, and rotations up to 360° on a grid, and predict the results of these transformations.

Learning Goals

The purpose of this learning situation is to have students:

  • visualize objects both in a two-dimensional space (that of two-dimensional shapes) and in a three-dimensional space (that of three-dimensional objects);
  • visualize the image of shapes following rotations, reflections and translations;
  • apply problem-solving strategies.

Learning Context

Prerequisites

In the primary grades, students have learned to perform translations and reflections of two-dimensional shapes, and have developed the ability to visualize the position of the image of a two-dimensional shape obtained as a result of either of these transformations. In the junior grades, students continue the study of transformations, adding performing rotations.

This learning task allows students, in a problem-solving context, to consolidate their understanding of the concepts of transformation, congruence, and area. It also allows them to perfect their ability to visualize the location of an object following a geometric transformation. 

To be able to carry out this learning situation, students must:

  • be able to identify congruent two-dimensional shapes;
  • be able to perform various transformations;
  • have an understanding of the concept of area.

Mathematical Vocabulary

pentomino, pentacube, flat pentacube, face, rotation, reflection, translation, congruence, area, square units

Material

  • interactive whiteboard
  • shoe boxes (one per team)
  • scissors (one pair per team)
  • large sheets of paper
  • 2 cm × 2 cm connecting cubes (60 per team)
  • masking tape
  • Appendix 5.1 (The Pentacube Box)
  • Appendix 5.2 (The 12 Pentominoes) (one copy per team)
  • Appendix 5.3 (The 29 Pentacubes)
  • Appendix 5.4 (Explanatory Notes)
  • grid paper

Optional Preparatory Activity

Duration: approximately 20 minutes

This optional preparatory activity introduces students to the 12 pentominoes in a problem-solving context and reviews the concepts of congruence and transformation.

Form teams of two students. Explain to them what a pentomino is using an example (see Appendix 5.2- The 12 pentominoes). Give each team two sheets of 2 cm × 2 cm grid paper and ask them to draw all the pentominoes they can find. Discuss as a class and make sure that the 12 pentominoes are identified. Explain to students that each of the pentominoes is associated, because of its shape, with one of the letters F, I, L, N, P, T, U, V, W, X, Y, and Z.

Before Learning (Warm-Up)

Duration: approximately 25 minutes

Write the word pentacube on the board. Ask students if they know what a pentacube is (see Appendix 5.4 - Explanatory Notes). Encourage them to think of other words that have the same prefix (for example, pentagon, pentomino, pentathlon) and recognize that the prefix pent- means “five''. Students should then be able to deduce that a pentacube is a three-dimensional object made up of five congruent cubes.

Ask a student to build a pentacube using connecting cubes and show it to the class. Point out that the cubes that make up a pentacube must be connected to each other by at least one face. Tell them:

  • that there are 29 different pentacubes (see Appendix - The 29 Pentacubes), of which 12 have two faces of five square units;
  • that these are generally called ”flat pentacubes“ and can, because of their shape, be associated one by one with the 12 pentominoes (see Appendix - The 12 Pentominoes) and the letters F, I, L, N, P, T, U, V, W, X, Y, and Z.

Form teams of two students and provide each team with 60 interlocking cubes, masking tape and a copy of Appendix - The 12 Pentominoes. Have them refer to the pentomino pictures in the appendix to construct a set of 12 flat pentacubes and identify each one, using a piece of masking tape, by the letter associated with it.

Note: If students have done the optional preparatory activity, they can use their drawings of the pentominoes instead of the 12 Pentominoes appendix. Alternatively, teams can be given sets of commercial pentacubes instead of constructing them.

Image there are two images. In the first, there are two people assembling cubes. In the second image, there are two people placing cube structures on corresponding images.

When teams are ready, hand out a copy of the Pentacube Box Appendix and present the problem in an interesting context. For example, tell students:

The other day I found a game in the back of a closet. It's a box with different openings through which you have to insert certain three-dimensional objects. (Show them such a game or show them the one in Appendix 5.1 - The Pentacube Box.) You may have played with a game like this when you were very young.

I thought it would be interesting to create a similar game using more complex geometric shapes - the 12 flat pentacubes - and offer Grade 3 students a chance to try it out. You must cut five openings in a cardboard box through which it will be possible to insert each of the 12 flat pentacubes. In order for the game to offer some challenge to those who try it, you must meet the following criteria:

Criteria

  • Each game must have only five openings: one opening on each of the four sides of the box and one on the top, but none in the bottom of the box.
  • All openings must have an area of 6 square units (one square unit is the area of one face of a connecting cube).
  • The 12 flat pentacubes must be inserted into one of the openings.

Ensure that students understand the task at hand by asking questions such as:

  • Who would like to explain the problem in their own words?
  • What criteria do you need to meet when creating the game?
  • What does an area of 6 square units mean?
  • Who will demonstrate how the pentacubes must pass through the openings?
  • How will you verify that your game meets the criteria?

Active Learning (Exploration)

Duration: approximately 50 minutes

Ask teams to determine the shape of each of the five openings before they begin cutting them out of the boxes. Provide them with 2 cm × 2 cm sheets of grid paper (Grid paper Appendix). To solve the problem, students can, through trial and error:

  • superimpose some pentacubes in order to find arrangements where one of the faces has an area of 6 square units;
  • draw shapes of openings with an area of 6 square units on blank paper or grid paper and then verify that the pentacubes can pass through each one.

Allocate sufficient time for students to explore openings. Circulate among students and intervene as needed. Pay particular attention to the strategies used to strategically select teams to present during the consolidation.

Possible Observations

Possible Interventions

Students design an opening with more than 6 square units.

Have them check the area of each of their openings and review the criteria.

Some students do not respect the fact that the pentacubes must lie flat in the opening.

Ask them to identify one of the flat pentacube and to reread the criteria to be met.

Students design five openings, but have one pentacube left to insert.

Encourage them to create an opening that will allow the remaining pentacube to be inserted and to redistribute the remaining pentacubes to eliminate one of the original five openings.

Students design their openings by considering only one of the two faces whose area measures 5 square units.

Encourage them to look closely at the pentacubes and analyze the similarities and differences between the two faces whose area measures 5 square units.

Note 1: The two faces are congruent, but are the image of each other, as if reflected in a mirror. Therefore, some pentacubes (F, L, N, P, Y, and Z pentacubes) can sometimes be inserted into the box through different openings depending on the face chosen.

Note 2: There are 35 different shapes of 6-square unit openings, corresponding to the 35 hexominoes. There are several combinations of five of these openings that can be used to insert the 12 flat pentacubes. The example below shows one of these combinations. In this example, the T, W and Y pentacubes can be inserted into the box through two different openings.

Example

Image there are five arrangements of six squares. Next to the first arrangements are the letters “ f ”, “ n ” and “ w ”. Next to the second arrangement are the letters “ t ”, “ x ” and “ y ”. Next to the third arrangement are the letters “ i ”, “ l ” and “ o ”. Next to the fourth arrangement are the letters “ p ”, “ v ” and “ w ”. Next to the fifth arrangement are the letters “ u ”, “ z ” and “ t ”.

Once students have determined the openings, distribute the shoe boxes and scissors and have them create their game. Remind students of the safety precautions to follow when using a sharp instrument.

Let students choose the strategy they will use to trace the shapes of the openings onto the box. For example, some students may place the flat pentacubes (individual or stacked) on the box and trace the outline. Others may cut out the shapes of the openings previously drawn on graph paper and trace their outline onto the box.

Ask students to prepare a presentation for the math exchange using their game or a large sheet of paper. Explain that they should explain the strategy they used to determine the shape of the five openings and present their mathematical findings, if applicable, using terms of causality or logical consequence (for example, ”If there are 12 pentacubes and only five openings, then some of the openings must allow for more than two pentacubes to be inserted.“).

Consolidation of Learning

Duration: approximately 15 minutes

Invite a few teams to present to the class.

Invite other students to ask questions of the presenting teams and share their observations. Advance the discussion by asking questions such as:

  • Who will explain to me in their own words the strategy used by this team?
  • Have other teams used the same strategy? Does this strategy seem effective to you?
  • Have other teams used the same five openings?
  • How can we justify that two openings are different?
  • What mathematical concepts were present in this activity? (Two openings are different if they are not congruent, that is, they cannot be superimposed.)

In creating the game, students use, sometimes unconsciously, a variety of mathematical concepts. In order to determine the shape of the openings, they must consider the concepts of area and congruence. The manipulation of the shapes and three-dimensional objects that the students transform in various ways encourages the development of visualization skills.

To enrich the consolidation of learning and make connections between concepts from Spatial Sense and Data, the teacher may choose to do the activity ”Popular Hexominoes“ (which is found below) at this time.

After the consolidation, ask students to exchange their game with another team and insert their 12 pentacubes flat through one of the five openings in the box they received. Challenge them to successfully insert all of them into the correct opening on the first try. Emphasize that they must carefully observe the shapes of the pentacubes and the openings and visualize the opening into which they will be able to insert a pentacube. Only when students are sure they have located the correct opening will they take the pentacube and attempt to insert it into the opening. This approach allows students to develop their ability to visualize the movement of shapes in space.

Differentiated Instruction

To Facilitate the Task

To Enrich the Task
  • Allow students to create their game with six openings instead of five.
  • Ask them to create a similar set using the five ”flat tetracubes“ (assembly of four flat cubes) and two openings of 5 square units.
  • Ask students to find two different combinations of five openings that allow the 12 pentacubes to be inserted using as many different openings as possible.
  • Ask students to determine the shapes of the openings from the representations of the flat pentacubes in the Appendix - The 29 Pentacubes (not from the pentacubes made of connecting cubes).

Note: This activity requires a higher degree of visualization.

  • Ask students to determine if it is possible to create a similar game using only four openings.

Note: Students will realize that this is impossible unless the area measurement of one of the four openings is 7 square units.

Follow-up at Home

Show students Figure 1 below and ask them which of cubes 1, 2 and 3 represents a transformation of the model cube.

Figure 1

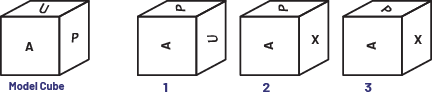Image There is a series of cubes. Under the first cube is written: model. The front view of the first cube is marked by an “ a ”; the top view is marked by a “ u ”; the side view is marked by a “ p ”. To the right of the cube, there are three other cubes. He front view of the first cube is marked by an “ a ”; the top view is marked by a " p "; the side view is marked by a “ u ”. The front view of the second cube is marked by an " a "; the top view is marked by a “ p ”; and the side view is marked by an “ x ”. The front view off the third cube is marked by an “ a ”; the top view is marked by a “ p ”; and the side view is marked by an “ x ”.

Invite students to create a similar problem at home and ask a family member to solve it. Emphasize the importance of paying attention to the orientation of the letters. If necessary, provide a copy of Figures 2 and 3 below. Students could choose to build a model cube from Figure 3 and write a letter on each face to help them determine how to place the letters on the faces of the cubes in Figure 2.

Figure 2

Image there is a series of four cubes. Under the first cube is written: model. Under the second cube is written: one. Under the third cube is written: two. Under the fourth cube is written: three.

Figure 3

A figure made up of six squares set in the shape of a cross.

Activity: Popular Hexominoes 

This activity is a follow-up to the learning situation and establishes a link between concepts from the Spatial Sense and Data strands. It consists of building a chart to present the range of openings chosen by the teams in the construction of their game and analyzing the results obtained.

Have students trace and cut out the shape of each of the five openings in their game. Prepare a table like the one shown below on large sheets of paper with the number or name of each team.

Image a table made up of 12 columns and eight rows. He first row identifies the teams and the shape of the unfolding. In the second row, there are ten arrangements of six squares. In the next four rows an “ x ” is placed in the column corresponding to the team and shape of the unfolding.

Display the table and ask a team to place the shape of one of their five openings in the table. Ask all teams that have used that opening shape to draw an X or place a sticky note under it in their team's corresponding square. Continue this process until all five openings from all teams are listed in the table. Total the number of times each opening has been used.

Encourage students to observe and analyze the data on the board. Ask various questions such as:

  • What conclusions can you draw from the data presented in the table?
  • How many different opening shapes were used in the construction of the games?
  • Which openings were used most often?
  • All teams used the opening Image A square of 2 units squared, labeled: “square root 2 units squared.” A square of 5 units squared labeled: “5 units squared.” A square of ten units squared labeled: “ten units squared.” or opening 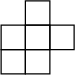Image A possible net of a cube consisting of 6 squares in an asymmetrical form. Two vertical squares attached to the side and from the bottom to 3 vertical squares. A final square attached to the side and middle of the three vertical squares.. Why? What is special about them? (These are the only two openings that allow the pentacube X to be inserted.)
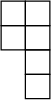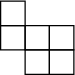  • Openings Image A possible net of a cube consisting of 6 squares in an asymmetrical shape. Two squares are attached vertically. To the side and starting from the top, four additional squares are attached vertically. and Image A possible net of a cube consisting of 6 squares in an asymmetrical shape. Two squares are attached vertically. To the side, two more squares starting with the last square. To the side, two more squares lined up with these two. have been used quite often. What is special about them? (They allow four pentacubes to be inserted.)
  • Why are some openings rarely used? (These are probably the ones that allow only one pentacube to be inserted)
  • Have other teams used the same five openings?

Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 65-76.