E1.3 Plot and read coordinates in all four quadrants of a Cartesian plane, and describe the translations that move a point from one coordinate to another.
Skill: Locating Coordinates in Each of the Four Quadrants of the Cartesian Plane
To locate a point in one of the four quadrants of a Cartesian plane, for example A (-3, -4), move along the horizontal axis three units to the left from the origin, then four units down.
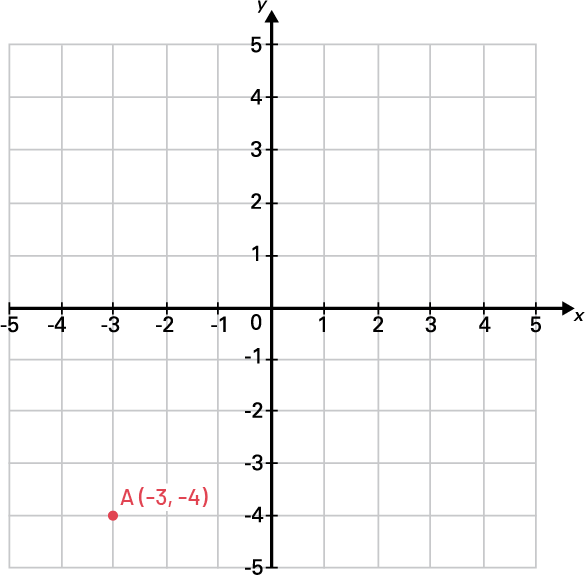
Students should be reminded of the importance of the order of the Cartesian coordinates. The first number, called the abscissa, indicates the horizontal position of the point relative to the origin and is located first. The second number, called ordinate, indicates its vertical position, and is located second.
While continuing to use the Cartesian plane, students may experience another conceptual difficulty that is linked to the use of the scale on the graduated axes. The difficulty arises when the students have to locate a point on the plane whose coordinates do not correspond to a vertical or horizontal grid line or to a number on the axes. For example, in a graph where the axes are graduated according by a scale of 2, only the even numbers are located along the axes. The odd numbers will not correspond to a grid line. The students may then believe that a point such as (7, 5), whose coordinates are each odd numbers, cannot be located on the plane since they do not see any odd numbers on the axes (grid lines representing them). Students must understand that it is possible to locate this point by mentally representing horizontal and vertical lines between the grid lines already there.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25-26.
Skill: Reading a Coordinate in the Four Quadrants of a Cartesian Plane
When reading the coordinates of a point located in any of the four quadrants of the Cartesian plane, we read the number that corresponds to the horizontal distance from the origin first and the number that corresponds to the the vertical distance second. We notice that when the point has a horizontal position that is to the right of the origin, it has a positive first coordinate. When it is to the left of the origin, it has a negative first coordinate. We further notice that if the point's vertical position is above the origin, it has a positive second coordinate. When its vertical position is below the origin, it has a negative second coordinate. Students must understand that Cartesian coordinates indicate points of intersection of the grid lines and not the squares formed by them.
Image there are two cartesian planes. In the first, there is a point “ a “ at the intersection minus two, three. In the second, here is a point “ b” at the intersection two, minus three.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25.
Skill: Describing Translations from One Point to Another Using Coordinates
To describe an oblique translation, one must verify both the horizontal movement and the vertical movement. To do this, students use symbolic notation in parentheses. For example, a translation three units right and two units down is represented symbolically by (3R, 2D) or (3→, 2↓) or (x + 3, y - 2). It is best to get the students used to always describing the translation by first indicating the horizontal movement and then the vertical movement.
Image There is a grid in which there are two identical figures. The first, being the initial figure, has the points “a ”, “ b ”, “ c ”, “ d ”, “ e ”, “ f ”, “ g ” et “ h ”. The second, being the complex figure, has the points “ a ” prime, “ b ” prime, “ c ” prime, “ d ” prime, “ e ” prime, “ f ” prime, “ g ” prime et “ h ” prime. Above the grid is written: Translation (opening parenthesis) six “d ”, four “ b ” (closing parenthesis) or (opening parenthesis) six, minus four (closing parenthesis).
In the junior grades, students can describe and perform horizontal, vertical, or oblique translations of two-dimensional shapes with an arrow. The arrow is usually placed outside the shape. The direction of the arrow corresponds to the direction of the translation and its length corresponds to the size of the movement.
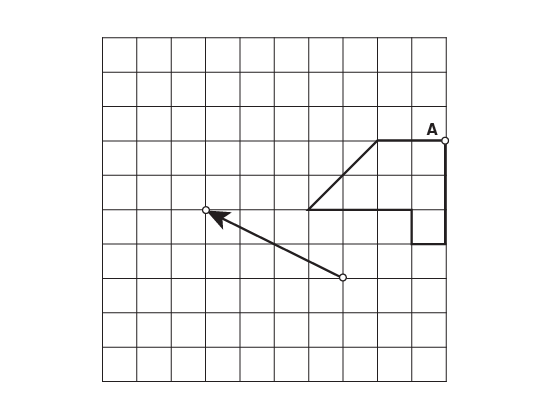Image a grid in which there is a figure marked by a point “ a ”. To the diagonal of the figure, there is an oblique arrow toward the upper left corner.
To determine the translation, students must determine the size of the horizontal and vertical movements represented by the arrow. For example, the arrow in the following plane describes the translation (4L, 2U) or (x -4, y + 2), which is a translation of four units to the left and two units up.
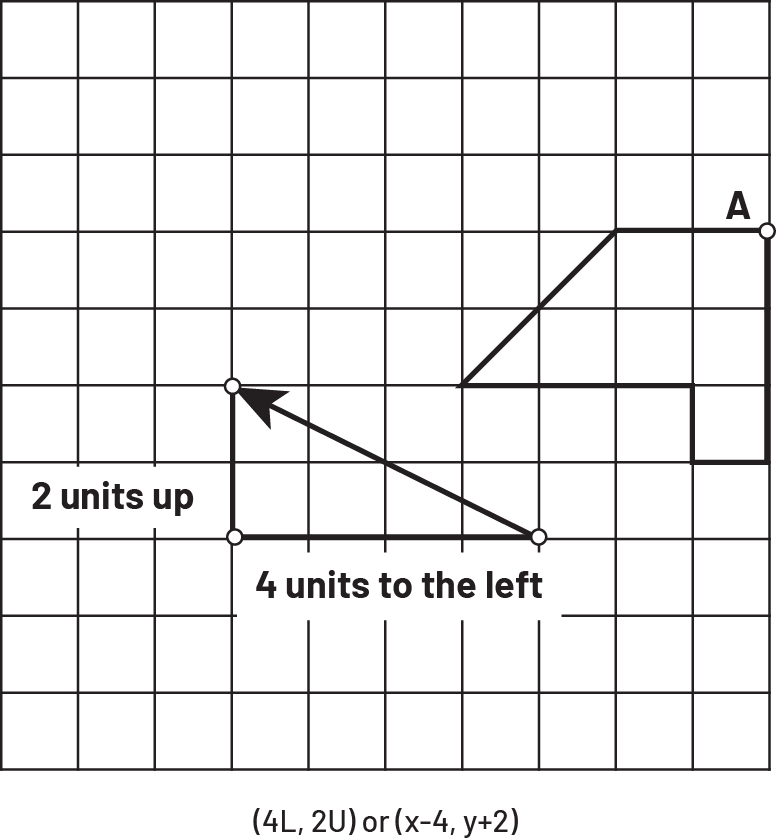Image a grid in which there is a figure marked by a point “ a ”. To the diagonal of the figure, there is an oblique arrow toward the upper left corner. The arrow forms one side of a right-angled triangle. On the side of the triangle is written: two units upwards; below the triangle is written: four units to the left. Below the grid is written (opening parenthesis) four “ g ”, two “ h ”(closing parenthesis).
During a translation, all the points of the original shape undergo the same movement, are moved in the same direction, and are equidistant from the corresponding points of the image.
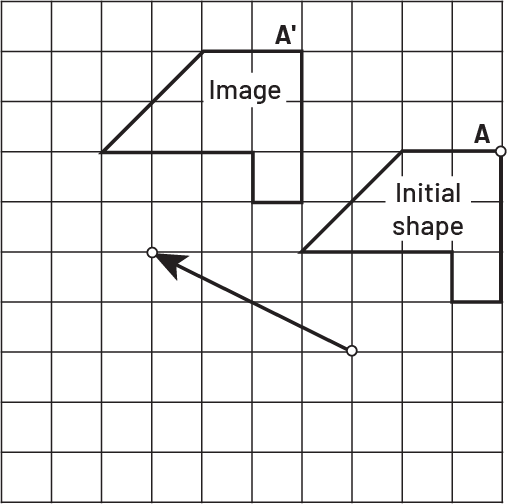Image A grid in which there are two figures. The first, being the intial figure, is marked by a point “ a ”. The second, being the image, is marked by a point “ a ” prime. Below the figures, there is an oblique arrow toward the upper left corner.
Each point of the original shape has undergone a translation of 4 units to the left and 2 units up.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 28-30.
Knowledge: Cartesian Plane
The Cartesian plane uses a coordinate system for precisely locating the position of a point in a plane.
In Grade 6, students use a Cartesian plane to more accurately locate a point in a plane. Two perpendicular axes are used to define the plane: one horizontal, identified by x and called the x-axis, the other vertical, identified by y and called the y-axis. The meeting point of these axes, called the origin, serves as a reference point. The axes divide the plane into four regions called quadrants.
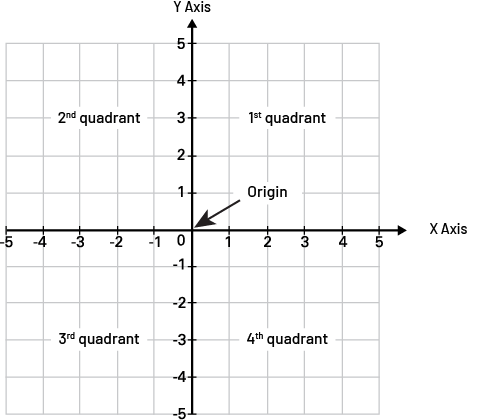Image there is a cartesian plane identifying four quadrants, going from the first in the upper right side, and going counter-clockwise. The five columns in the “ x ” axis and the five rows in the “ y ” axis are numbered. The origin is identitfied by an arrow.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 24.
Knowledge: A Coordinate
The Cartesian coordinate system is used to locate a point in the Cartesian plane. The coordinates are written in parentheses and are separated by a comma as follows: point A (2, 4). By convention, the first number, called the abscissa, indicates the horizontal position of the point with respect to the origin, and the second, called the ordinate, indicates its vertical position.
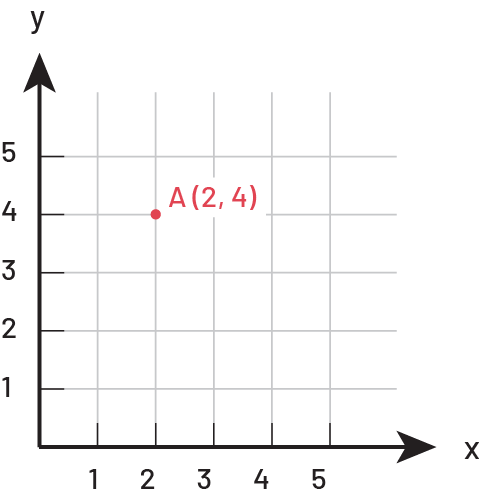
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 25.
Knowledge: Translation
The translation is defined by its size and direction (represented symbolically by coordinates or by an arrow). It represents a linear, horizontal, vertical, or oblique (diagonal) movement in which the original shape and the image are congruent. The distance between each point on the original shape and the corresponding point on the image is constant. The orientation of the image is the same as the orientation of the original shape.
Image there are two identical figures on a grid. The point “ a ” on the first figure is tied to the point “ a ” prime on the second. Another parallel line ties the base of the two figures. To the diagonal, there is an oblique arrow towards the lower right. Below the grid is written: Translation (opening parenthesis) four “ d ”, four “ b ” (closing parenthesis) or (opening parenthesis) four, minus four (closing parenthesis).
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 36-37.