E2.1 Measure length, area, mass, and capacity using the appropriate metric units, and solve problems that require converting smaller units to larger ones and vice versa.
Skill: Choosing Appropriate Metric Units
The act of measuring involves a series of decisions, reflections, and actions that lead to obtaining and communicating an accurate and appropriate measurement for a given context. This involves a number of steps that are the same for all the attributes under study in the Junior Division: length, area, volume, angle, capacity, mass, temperature, and time. Although the number and identification of these steps vary somewhat among researchers, they can generally be articulated in sequence as follows:
Steps in the Act of Measuring
- determine the attribute to be measured;
- choose the unit;
- determine the measurement;
- communicate the result.
The first step in any problem situation involving the act of measuring is to determine the attribute of the object to be measured. For example, is it length, area, capacity, mass? To be able to determine which attribute to measure in a given situation, students need to have a clear understanding of each attribute. Teachers should therefore provide students with a variety of learning situations that encourage them to determine the various attributes of an object and to choose the one that will allow them to solve the problem.
Choose the Unit
The second step in the act of measuring is to choose an appropriate non-standard or standard unit for the attribute of the shape, object, or substance, to be measured. To do this, it is important to choose a unit that is appropriate to the situation. In addition, it is generally preferable to use a single unit. Finally, it is also important that the choice of unit takes into account the degree of precision of the measurement being sought (for example, a mass measurement to the nearest kilogram or gram).
When first exploring an attribute of a shape, object, substance, or measurable period, it is best for teachers to encourage students to choose a non-standard unit first, so that they can better understand the meaning of the attribute and its measurement. Later, they can point out the limitations of the chosen unit and the advantages of using a standard unit.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 83-87.
Precision is not always necessary and may be a waste of time. It could also complicate the measurement.
The same metric prefixes apply to all attributes (except time) and indicate the relationships between units. A unit just to the left of a particular unit in the chart is 10 times greater, and the unit just to its right is 10 times less.
| Metric prefix | kilo | hecto | deca | No prefix | deci- | centi- | milli- |
|---|---|---|---|---|---|---|---|
| Unit value | 1000 units | 100 units | 10 units | 1 unit | \(\frac{1}{10}\) unit | \(\frac{1}{100}\) unit | \(\frac{1}{1000}\) unit |
| Place value | thousand | hundred | ten | one | one tenth | one hundredth | one thousandth |
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Skill: Measuring Length, Area, Mass, and Capacity
Determine the Measurement
The third step in the act of measuring is to determine the measurement of an attribute of a shape, object, or substance by quantifying it in terms of a unit.
Steps in the Act of Measuring
- determine the attribute to be measured;
- choose the unit;
- determine the measurement;
- communicate the result.
Using a Measuring Tool
Many measuring tools (for example, ruler, scale) have been designed to determine the measurement of various attributes in terms of standard units. Although this strategy provides a quick measurement, it requires the user to have a good sense of measurement and abstract thinking. To help students understand the importance of these tools and how to use them correctly, the teacher can suggest that they make one.
In the primary grades, it is important that students learn to use some of the common measuring tools such as those listed in the table below, taking into account the degree of precision sought and the importance of accuracy of measurement.
| Attributes | Tools |
|---|---|
|
Length |
|
|
Mass |
|
|
Capacity |
|
In any situation involving measurement, the degree of precision sought determines the size of the unit that should be used and should be decided based on the use or the intention of the measurement. For example, in some situations it may suffice to know that the height of a door frame is about 2 m. This measurement, given to the nearest metre, is approximate, with a low degree of precision. The height of the door frame is likely to be a little less or a little more than 2 m. If a door is to be fabricated to fit into the door frame, it would be necessary to obtain a more accurate measurement. To achieve this, we would use a smaller unit - a unit corresponding to a fraction of a metre (for example, centimetres). We could then determine that the height of the door frame measures, to the nearest centimetre, 213 cm, for example.
Students should recognize the importance of choosing a unit that matches the degree of precision imposed, explicitly or implicitly, by the measurement situation. For example, to determine the time it takes to run a 100-metre race, students may choose to use a stopwatch to obtain a measurement to the nearest second. On the other hand, students should recognize that during the Olympic Games, it is necessary to measure the time required for athletes to run the 100-metre race to the nearest \(\frac{1}{1000 }\)th of a second.
The accuracy of the measurement will depend, among other things, on how well the measuring tool is used. If the tool is not used correctly. To help students understand the proper way to use a given measuring tool, teachers can first model using it. In the following, some details about how to use certain tools are presented.
To use a ruler correctly, you must:
- align one end of the shape or object with the zero point of the tool (or the beginning of the graduations);
- make sure that the line of sight on the other end of the shape or object is at a 90° angle to the ruler (see Parallax Error below);
- count on the ruler the units that go from one end of the shape or object to the other.
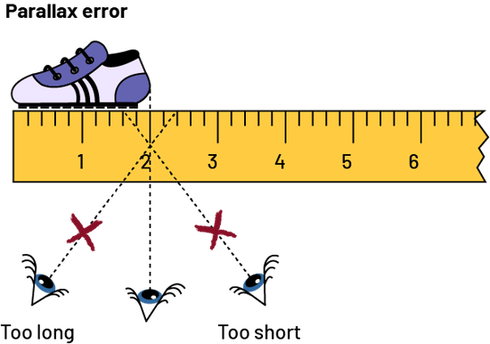 Image there is a six centimeter ruler. Above the rule, there is a show. Below, there are three eyes. From each eye, there is a dotted line tied to the ruler. There is an “ x ” on the first and third dotted line.
Image there is a six centimeter ruler. Above the rule, there is a show. Below, there are three eyes. From each eye, there is a dotted line tied to the ruler. There is an “ x ” on the first and third dotted line.
To properly use a two-pan scale, you must:
- place the balance on a flat horizontal surface;
- make sure the scale is balanced before placing the object to be measured on one of the pans;
- place the object to be measured on one of the pans and, in the other pan, put one of the chosen mass units (for example, a mass of 1 g);
- add objects of known mass until the two pans are in balance again;
- count the units of known mass used.
To properly use the triple beam scale, you must:
- place the balance on a flat horizontal surface;
- make sure the arrow points to zero before placing the object to be measured on the pan;
- place the object to be measured in the centre of the pan;
- move the sliding masses one at a time, always starting with the largest mass (for example, the 100 g mass, then the 10 g mass, and finally the 1 g mass) and always making sure to place the masses in one of the notches;
- make sure the arrow is always pointing above zero before moving a mass to the next notch;
- if the arrow points below zero, move the mass back one notch and move the next (smaller) mass;
- proceed in this way until the arrow points to zero;
- read the mass of the object according to the graduations where each of the three masses are inserted.
To properly use a graduated cylinder, you must:
- make sure to place the cylinder on a flat horizontal surface;
- slowly pour the liquid in, taking care not to create air bubbles;
- make sure you are positioned to read the volume of liquid with the meniscus in mind;
- read the volume of liquid according to the scale on the wall of the cylinder (for example, 100 mL).
The curvature of the surface of a liquid in a container is called a meniscus. In a graduated cylinder, a liquid, such as water, sticks to the wall and the meniscus takes on a concave shape. The reading of the volume of liquid must be taken at the lowest point of the meniscus.
 Image there is a filled test tube. To the right of the test tube is an eye and an arrow pointing to the curve in the test tube, being the meniscus.
Image there is a filled test tube. To the right of the test tube is an eye and an arrow pointing to the curve in the test tube, being the meniscus.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 89-98.
Communicate the Result
Once students have determined the measurement of an attribute of an object, the teacher should encourage them to demonstrate their understanding of the resulting measurement by clearly communicating their result using appropriate vocabulary and units.
Steps in the Act of Measuring
- determine the attribute to be measured;
- choose the unit;
- determine the measurement;
- communicate the result.
For example, after determining that the height of the column of liquid (mercury or alcohol) in the classroom thermometer is 20, some students may be inclined to simply say, ”It's 20.“ Teachers should encourage them to always express their result by pointing out the attribute and object or substance being measured, as well as the unit used (for example, ”The height of the liquid in the thermometer tells us that the temperature in the classroom is currently 20°C.“) Teachers can also encourage them to demonstrate their understanding of this result by comparing it with another measurement or situation (for example, ”It's a nice temperature; it's not as hot as it was outside.“) The table below provides various examples of clear communication involving the different measurement attributes under consideration.
|
Measured Attribute |
Selected Unit |
Quantity |
Communication of the Result |
|
Length of a notebook |
centimetre |
25 |
The length of the notebook is 25 cm. |
|
Mass of a bucket filled with water |
kilogram |
8 |
The bucket filled with water has a mass of 8 kg. |
|
Surface area of a box |
square centimetre |
168 |
The surface area of the box is equal to 168 cm2. |
|
Capacity of a coffee cup |
millilitre |
300 |
The coffee cup has a capacity of 300 mL. |
Teachers should ensure that students can read symbols correctly when communicating their results orally. For example, they should say:
- "The length of the notebook is 25 centimetres." not "The length of the notebook is 25 c-m.";
- "The area of the surface of the box is equal to 168 square centimetres." not "The area of the surface of the box is equal to 168 c-m to the exponent 2."
They should also ensure that the students know how to correctly write the symbols representing the various units while respecting the established conventions. To help students develop the ability to clearly communicate a measurement result during mathematical conversations, teachers should ask questions using words that clearly refer to the attribute being measured. For example, they should ask, ”What is the capacity of the glass?“ and not ”How much water does the glass hold?“; ”Which apple has the greatest mass?“ and not ”Which apple is the heaviest?“
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 102-104.
Skill: Solving Problems That Require Conversion of Smaller Units to Larger Units and Vice Versa
Inverse Relationship
The number of units required to determine the measurement of an attribute is inversely proportional to the size of the unit used. In other words:
• the smaller the unit used, the greater the number of units required to determine the measurement of the attribute;
• the larger the unit used, the smaller the number of units required to determine the measurement of the attribute.
For example, if the duration of the same activity is measured once in minutes and then again in seconds, the number of seconds will be greater than the number of minutes because the second is a smaller unit than the minute. Although the concept of an inverse relationship may seem obvious in this type of situation, it is problematic for many students who are familiar with direct relationships (for example, the greater the distance to be travelled by car, the greater the duration of the trip). In order to help them understand this concept, teachers should present them with a variety of concrete measurement situations that encourage them to make this connection.
Example
A teacher asks students to determine the capacity of a container. She gives half of the students a small cup and the other half a larger cup. During the follow-up conversations, some of the students indicate that the capacity of the container is 10 cups while others indicate that it is 30 cups. The teacher then prompts students to relate the size of the unit used to the number of such units required to determine the capacity of the container by asking questions such as:
- Why didn't you all get the same measurement of capacity? (Because we didn't all use the same size unit.)
- Who found the most units? (Those who used the smaller cup as a unit.)
- Who got the smallest number of units? (Those who used the larger cup as a unit.)
- Why is this so? (Because it takes more small cups than large cups to fill the container.)
In order to encourage students to think further and to propose a conjecture, the teacher can present the students with a cup whose size is between the small and the large cup and ask them to estimate the capacity of the container according to this new unit, and to explain their reasoning.
”I think the capacity of the container is about 20 of these cups because this cup is smaller than the larger cup, so we will need to use more than 10, which was the number of larger cups needed. On the other hand, since it is larger than the smaller cup, we will need to use less than 30, which was the number of smaller cups needed.“
Finally, the teacher encourages students to formulate a generalization by asking questions such as:
- What happens to the number of units needed when the size of the unit increases? Why? (The number of units needed decreases. Fewer units are needed when the unit is larger.)
- What happens to the number of units needed when the size of the unit decreases? Why? (The number of units needed increases. More units are needed when the unit is smaller.)
- Can you explain in your words the relationship between the size of a unit and the number of units required to measure an attribute using that unit? (The smaller the unit used to measure the attribute, the greater the number of units required.)
It is important for teachers to expose students to this type of reasoning in a variety of situations to ensure that they understand this inverse relationship and recognize that it applies to the measurement of any attribute. Teachers can also use a variety of measurement situations to test students' understanding of this inverse relationship by asking them to test the reasonableness of the equivalence of any two measurements. For example, during a measurement activity, a student states, ”The container has a capacity of 1200 mL, which is equivalent to 12 000 cL.“ The teacher will ask other students what they think of this statement and will lead a mathematical discussion to get them to use the inverse relationship to show that the statement is false.
”If this container has a capacity of 1200 mL, there is no way it can also be 12 000 cl, because centilitres are larger than millilitres; therefore, I have to use fewer cl to fill the container.“
Relationships between Conventional Units
When students have a good grasp of the concept of an inverse relationship between the number of units required to determine a measurement and the size of that unit, they can more easily understand and establish relationships between some of the conventional units.
In order for students to develop an understanding of these relationships, teachers must provide learning situations that allow them to make sense of standard units as well as to explore different strategies for converting from one unit to another. These strategies are based on the recognition that any unit can be expressed:
- as a multiple of a smaller unit (for example, one metre equals 1000 millimetres);
- as a fraction of a larger unit (for example, one metre is \(\frac{1}{1000}\) of a kilometre).
Relationships between units of Length, Mass and Capacity
The fact that the various standard units associated with the attributes length, mass , and capacity are part of a decimal system of units is used to establish equivalence relationships between these units. For example, since the gram (g) is 10 times larger than the decigram (dg) and \(\frac{1}{10}\) as large as the decagram (dag), the following equivalence relationships can be established: 1 g = 10 dg, 1 g = 0.1 dag. Students need to explore a number of different learning situations with concrete materials in order to develop a good understanding of these equivalence relationships. In order to be able to move easily between the various units of measurement, they also need to have a good grasp of the concept of an inverse relationship.
Example 1
A teacher gives each team a tape measure and asks them to cover a tenth of it with cardboard. He then asks the following question:
- What is a tenth of a metre? (1 dm, 10 cm or 100 mm)
- What relationships can be established between decimetres, centimetres and millimetres? (1 dm = 10 cm, 1 dm = 100 mm, 10 cm = 100 mm)
Note: The reasoning behind these relationships is based on the property of transitivity.
The teacher can then encourage students to discover other relationships between units of length by asking them to cover one tenth of a decimetre, one tenth of a centimetre, one hundredth of a metre, or one hundredth of a decimetre.
Example 2
Ask students to pour a litre of water into a graduated cylinder, then record the volume of water in the cylinder in centilitres and millilitres. Point out the following equivalencies:
1 L = 100 cl, 1 L = 1000 mL.
Encourage students to use their understanding of the inverse relationship to establish relationships between the units used by asking questions such as:
- Why is the number corresponding to the measurement of the volume of water in the cylinders smaller when the volume is expressed in centilitres than when it is expressed in millilitres? (The unit centilitres is larger than the unit millilitres, so fewer centilitres than millilitres are needed to represent the same volume of water.)
- How can the number of centilitres be represented as millilitres? Explain your thinking. (The volume of water in the cylinder was noted to be 1000 mL or 100 cl. Therefore, there is \(\frac{1}{10}\) the number of centilitres than millilitres of water in the test tube.)
- Is the unit centilitre much larger than the unit millilitre? How do you know? (Since the number of centilitres of water in the cylinder is \(\frac{1}{10}\) the number of millilitres, we can conclude that the unit centilitre is 10 times larger than the unit millilitre.)
- How can you symbolically describe the relationship between centilitres and millilitres? (1 cL = 10 mL)
Prompt students to demonstrate their understanding of unit relationships by applying the same type of reasoning to another situation. For example, they can point out that the decilitre is a unit 10 times larger than the centilitre, and then ask, ”How many decilitres of water do you think are in the cylinder? Why?“ (We know that there are 100 cl of water in the cylinder. Since the unit decilitre is 10 times larger than the unit centilitre, the number of decilitres of water in the cylinder must be \(\frac{1}{10}\) of 100. Therefore, there must be 10 dl of water in the cylinder.)
As students explore such learning situations, encourage them to apply their understanding of the relationships between the units to propose a conjecture and then to formulate a generalization. For example, with the understanding that one millimetre is one thousandth of a metre (1 mm = 0.001 m), ask students to make a conjecture about how many litres are in one millilitre (one millilitre is one thousandth of a litre or 1 mL = 0.001 L). Ask students to verify their conjecture and then guide them in making a generalization, namely, that the prefix milli-placed in front of a unit designates a measurement equivalent to one thousandth of that unit. For example, a milligram is one thousandth of 1 gram (1 mg = 0.001 g).
By the end of the Junior Division, students should understand that the prefix:
- milli- placed in front of a unit designates a measurement equivalent to one thousandth of the base unit (for example, 1 mg = 0.001 g);
- centi- placed in front of a unit designates a measurement equivalent to one hundredth of the base unit (for example, 1 cg = 0.01 g);
- deci- placed in front of a unit designates a measurement equivalent to one tenth of the base unit (for example, 1 dg = 0.1 g);
- deca- placed in front of a unit designates a measurement equivalent to 10 times the base unit (for example, 1 dag = 10 g);
- hecto- placed in front of a unit designates a measurement equivalent to 100 times the base unit (for example, 1 hg = 100 g);
- kilo- placed in front of a unit designates a measurement equivalent to 1000 times the base unit (for example, 1 kg = 1000 g).
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 60-67.
Knowledge: Length
Length is a measure in one-dimensional space. A length can refer to:
- the size of a line segment, namely, the distance between two points;
- the distance between two parallel lines or two parallel planes;
- a perimeter;
- a height, a depth, a thickness, a width, a size
Note: For some students, these different terms associated with length may be confusing.
Examples
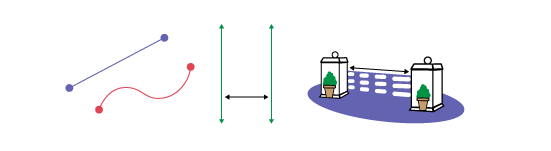 Image there are three images. The first is a straight line and a curved line. The second is of two parallel vertical lines; between the two lines, there is a horizontal arrow. The third is of a fence; there is a line along the longest side of the fence.
Image there are three images. The first is a straight line and a curved line. The second is of two parallel vertical lines; between the two lines, there is a horizontal arrow. The third is of a fence; there is a line along the longest side of the fence.
The perimeter is the length around a two-dimensional shape, or any three dimensional object.
 Image There are two symbols. The first is a stop sign outlined by a dotted line. The second is of a stick of butter. There is a dotted line along one of the longest and one of the shortest sides.
Image There are two symbols. The first is a stop sign outlined by a dotted line. The second is of a stick of butter. There is a dotted line along one of the longest and one of the shortest sides.
The length of a book becomes its height when stored upright on a shelf, just as its thickness becomes its width.
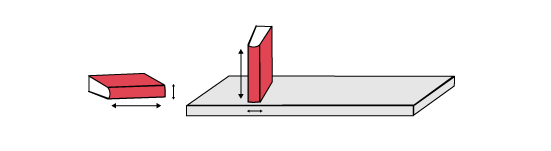 Image there are two images. The first is of a book laying flat. There is an arrow along the longest and the shortest sides. The second is of a book placed vertically on a shelf. There is an arrow along the longest and the shortest sides.
Image there are two images. The first is of a book laying flat. There is an arrow along the longest and the shortest sides. The second is of a book placed vertically on a shelf. There is an arrow along the longest and the shortest sides.
Source: translated from Fiche de la 4e à la 6e année, Attribut longueur, p. 2.
Knowledge: Area
Area refers is a measure of the space inside size of a two-dimensional surface or space. The size of a piece of land and the size of a country are examples of area.
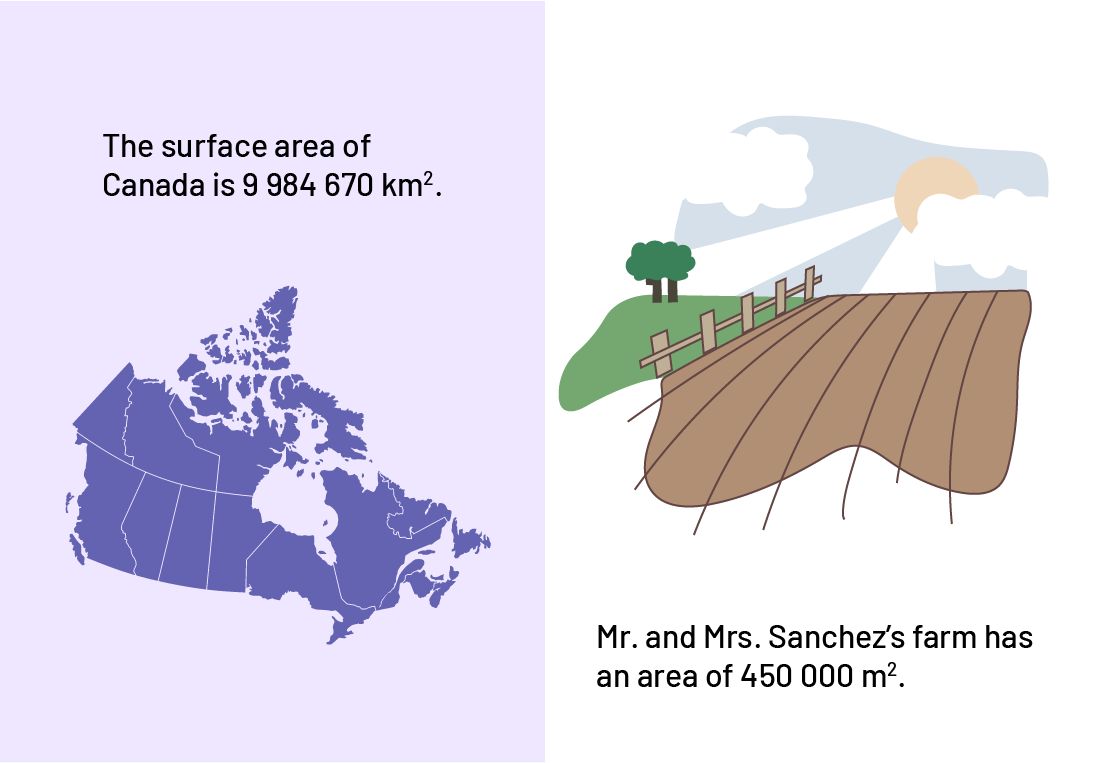 Image There are two images. The first is of a map of Canada. Above the image is written: the surface area of Canada is 9 million 984 thousand 670 cubic kilometers. The second image is of a field with a fence under a sunny sky. Below the image is written: Mister and Missus Sanchez’s farm has an area of 450 thousand 000 square meters.
Image There are two images. The first is of a map of Canada. Above the image is written: the surface area of Canada is 9 million 984 thousand 670 cubic kilometers. The second image is of a field with a fence under a sunny sky. Below the image is written: Mister and Missus Sanchez’s farm has an area of 450 thousand 000 square meters.
Source: translated from Fiche de la 4e à la 6e année, Attribut aire, p. 2.
Knowledge: Mass
Mass refers to the amount of matter in an object. Only the type of matter that makes up an object influences its mass. Thus, the mass of an object does not vary depending on where on Earth (or in space) it is located.
The mass of an object is determined using a scale or balance, such as a triple-beam scale or a two-pan scale.
Note: Mass should not be confused with weight. The weight of an object refers to the force exerted on that object by a celestial body. It is determined using a dynamometer and is expressed in newtons (N). The weight of an object varies depending on its mass and the place on Earth (or in space) where it is located.
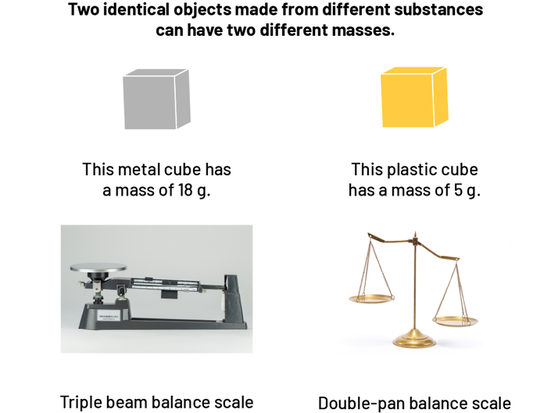 Image There are four images. The first two are of a cube. Below the first one is written: this metal cube has a mass of 18 grams. Below the second one is written: this plastic cube has a mass of 5 grams. The third image is of a triple beam balance scale. The fourth image is of a double-pan balance scale. Above the images is written: two identical objects made from different substances can have two different masses.
Image There are four images. The first two are of a cube. Below the first one is written: this metal cube has a mass of 18 grams. Below the second one is written: this plastic cube has a mass of 5 grams. The third image is of a triple beam balance scale. The fourth image is of a double-pan balance scale. Above the images is written: two identical objects made from different substances can have two different masses.
Source: translated from Fiche de la 4e à la 6e année, Attribut masse, p. 2.
Knowledge: Capacity
The capacity of a container is the maximum amount it can hold.
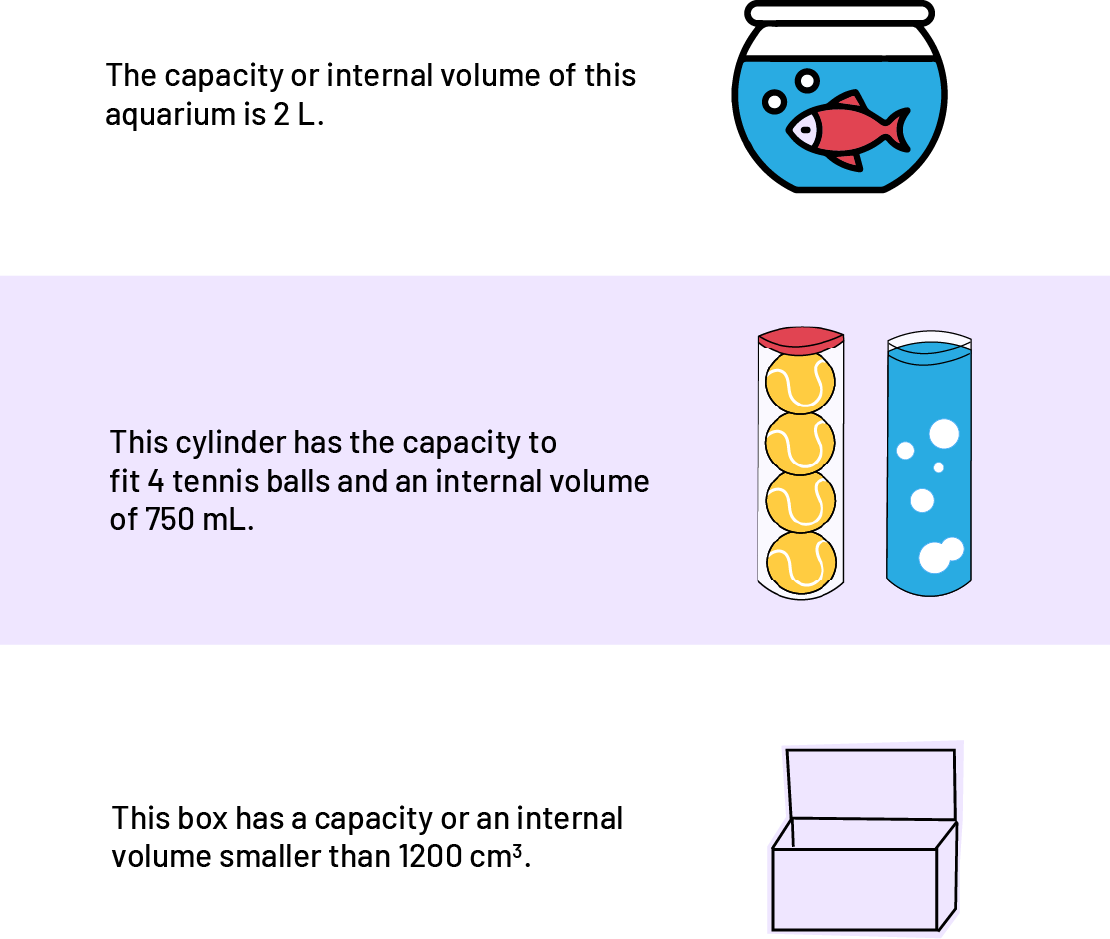 Image three images one under the other. The first, a fish bowl with the text, “ The capacity of this aquarium is two litres of water. ” Underneath are two images of tennis ball cans. One with balls, the other with a liquid. The text to the left reads, “This cylinder has 4 tennis balls“ m ” “ l ”. Underneath is an open box with the text to the left stating, “This box has a capacity smaller than 1200 cm3.”
Image three images one under the other. The first, a fish bowl with the text, “ The capacity of this aquarium is two litres of water. ” Underneath are two images of tennis ball cans. One with balls, the other with a liquid. The text to the left reads, “This cylinder has 4 tennis balls“ m ” “ l ”. Underneath is an open box with the text to the left stating, “This box has a capacity smaller than 1200 cm3.”
Source: translated from Fiche de la 4e à la 6e année, Attribut capacité, p. 2.
