La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E2.3 Use the properties of supplementary angles, complementary angles, opposite angles, and interior and exterior angles to solve for unknown angle measures.

Skill: Using Properties of Angles to Determine Missing Angle Measurements

Angle properties can be used to determine unknown angles.

  • A straight angle measures 180°: this property is used to determine the measurement of a supplementary angle and is applied when determining the exterior angles of a polygon.
  • A right angle measures 90°: this property is used to determine the measurement of a complementary angle.
  • Interior angles of quadrilaterals sum to 360°; this property is used to find an unknown angle in a quadrilateral.
  • Interior angles of triangles sum to 180°; this property is used to find an unknown angle in a triangle.

Angle properties can also be used to determine other unknown measures (for example, the exterior angle measurements of a polygon) or to explain why opposite angles are equal.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

For example, we observe the angles of this triangle.

  • ∠A, ∠B and ∠C are inside triangle △ABC
    • ∠A = 110°
    • ∠B = 50°
    • ∠C = ?°
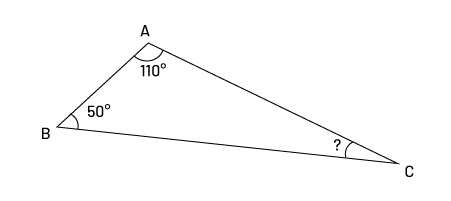Image a triangle, the peaks being “ a “ which has an angle of 110 degrees, “ b “ which has an angle of 50 degrees and “ c “ the angle of which is not written.

The student who has generalized and understands that the sum of the interior angles of all triangles equals 180 degrees can find the measurement of the unknown angle by subtracting the sum of the two known angles from 180.

Consult this document to become familiar with the sum of the interior angles of polygons. Note that it is important to discover and generalize these sums through exploration activities.

Knowledge: Angle Measurement

It is important for the student to understand that the angle measurement states the magnitude of an ”opening“.

The angle can be defined by:

  • two line segments;
  • two rays having a common endpoint;
  • two half-planes that intersect each other.
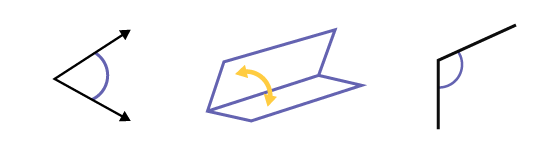Image there are three illustrations. The first is of an acute angle formed by two arrows. The second is of an open angle, indicated by an arrow. The third is of an obtuse angle formed by two line segments.

During the exploration of angles, common student errors are related to misrepresentations and representations. Some students believe that the angle gets larger if the rays representing it are drawn longer because the opening looks wider.

For example, I think angle A shown below is smaller than angle B because the lines that form angle A are shorter.

There are two angles, being “ a ” which is smaller than “ b ”.

When students are provided with meaningful contexts to practice measuring and comparing angles that are represented in a variety of ways, they develop a deeper understanding of the concept of angle and angle measurement. In the example below, the angles are equivalent; however, the segments that make up the angles are different lengths.

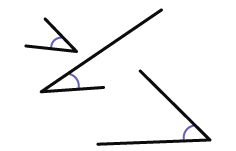
There are three angles for which the line segments are all different.

When students are able to compare the magnitude of angles without regard to the length of the rays that form those angles, they are ready to begin measuring angles accurately.

Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 15-19.

Knowledge: Properties of Angles

Adjacent Angles

Two angles are adjacent if they have the same vertex and a common side and if they lie on either side of the common side.

For example, ∠zoy is adjacent to ∠yox.

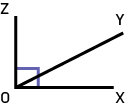 There are two angles side-by-side to form a square angle.
Supplementary Angles

Two angles are supplementary when the sum of their measurements is equal to 180o.

For example, ∠xoy and ∠yoz are supplementary and adjacent.

 There are three-line segments forming a flat angle.
Complementary Angles

Two angles are complementary when the sum of their measurements is 90o.

For example, ∠yoz and ∠xoy are complementary and adjacent.

 Two angles side-by-side forming a square angle.
Vertex Opposite Angles

Two angles formed by the intersection of two lines or four line segments oriented in the same direction in pairs. They are always congruent.

For example, ∠xly is opposed to ∠wlv.

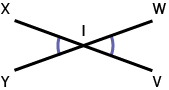 There are two-line segments which intersect creating two opposing angles.

Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Document d'appui, Fascicule 1, p. 16.

Knowledge: Interior and Exterior Angles

Interior Angles

Students should be able to identify the measures of the vertex angles in a two-dimensional shape.

In the examples below, we see that the triangle has three interior angles and the quadrilateral has four interior angles.

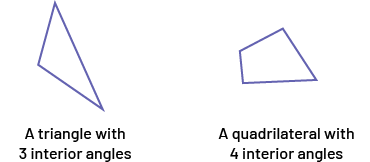Image there are two figures: a triangle and a quadrilateral. Below is written: a triangle with three internal angles. Below the second is written: a quadrilateral with four internal angles.

When two line segments or rays are drawn from a common point, they actually form two different angles (figure below), the interior and the exterior angle.

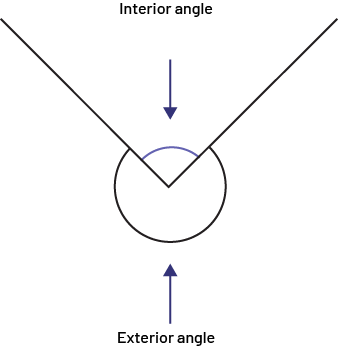Image there is a projecting angle, one inside the segments and a recessed angle, outside the segments, both marked by an arrow.

There is an exceptional case where the two line segments or rays do not form two different angles (figure below). This is the case when the two line segments are aligned, since they then form two equal angles of 180° (straight angles).

There is an angle on either side of a horizontal line, measuring a flat angle.

By convention, an arc is drawn between the two line segments or rays to indicate the angle being discussed. It is important that students do not associate the size of the arc with the measurement of the angle. For example, the two angles shown below are congruent even though the arcs may give the impression that one angle is larger than the other.

There are two angles, of which one arc is longer than the other.

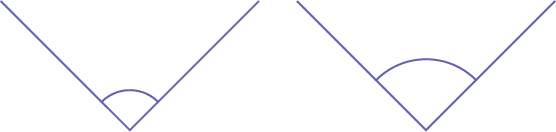
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 23-24.

Exterior Angles

An exterior angle is the angle between a side of a polygon and a line that extends outward from an adjacent side.

In a polygon, the exterior angle and the adjacent interior angle are supplementary, that is, their sum is always 180°.

The sum of the exterior angles of a polygon is always 360°.

Examples of Polygons

Hexagon

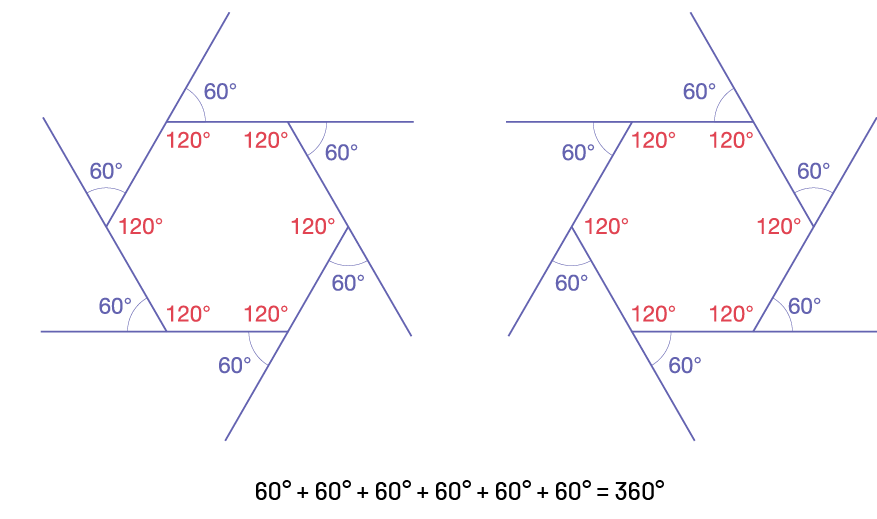Image there are two hexagons for which the angles are measured counterclockwise to the needles of a watch in the first figure and clockwise to the needles of a watch in the second. Below the hexagon is written: 60 degrees plus 60 degrees plus 60 degrees plus 60 degrees plus 60 degrees equals 360 degrees.

Rectangle

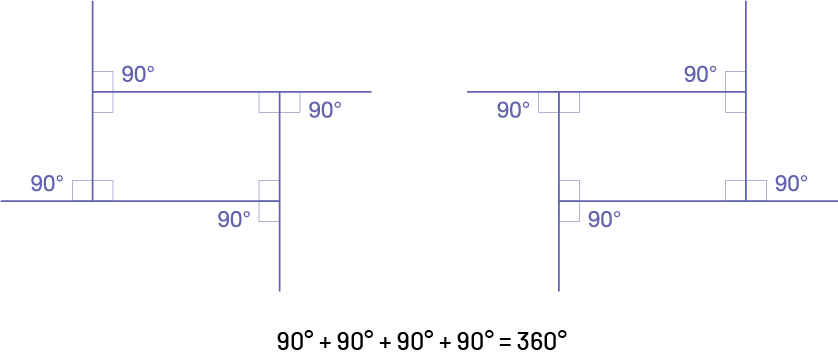Image there are two identical rectangles in which the angles are measured counter-clockwise to the needles of a watch in the first figure, and clockwise in the needles of a watch in the second. Below the figure is written: 90 degrees plus 90 degrees plus 90 degrees plus 90 degrees equals 360 degrees.

Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).