E2.4 Determine the areas of trapezoids, rhombuses, kites, and composite polygons by decomposing them into shapes with known areas.
Skill: Determining the Area of Trapezoids, Rhombuses, Kites, and Composite Polygons by Decomposing Them into Shapes with Known Areas
In measurement, additivity refers to the concept that the measurement of an attribute of an object is equal to the sum of the measurements of its parts.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 52.
Students who understand the fundamental concept of additivity realize that the area of a polygon is equal to the sum of the areas of its parts.
For example, if students are asked to determine the area of the polygon below, they would decompose it into a rectangle and a triangle, then determine the area of each and add the two areas.
Students can then use their knowledge of the area of a triangle, a square, and a rectangle to decompose other quadrilaterals (trapezoid, rhombus, and kite) or complex polygons.
In addition, students who understand the concept of conservation of area realize that the area of a surface remains the same whether the surface is moved or decomposed.
Source: translated from Fiche de la 4e à la 6e année, Attribut aire, p. 3.
Example of the concept of conservation of area
The area of each of Shapes 1 and 2 below is the same as the area of the square because all three shapes are constructed from the same seven pieces of a tangram set.
Teachers should take advantage of a variety of situations to encourage students to recognize that there is a close connection between the concept of additivity and the concept of conservation of area.
For example, when students construct different shapes from the seven pieces of a tangram set, it prompts them to recognize that the overall area of every constructed shape is the same (conservation of area) and equals the sum of the areas of each of the seven parts that compose it (additivity).
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Mesure, p. 50, 53-54.
Students can determine the area of a trapezoid by breaking it down into shapes with known area formulas.
There are different ways of decomposing and recomposing trapezoids to form rectangles, parallelograms or triangles. The different composition strategies create unique formulas, but the formulas will be equivalent.
- A trapezoid can be broken down into two triangles and a rectangle whose areas are then combined.
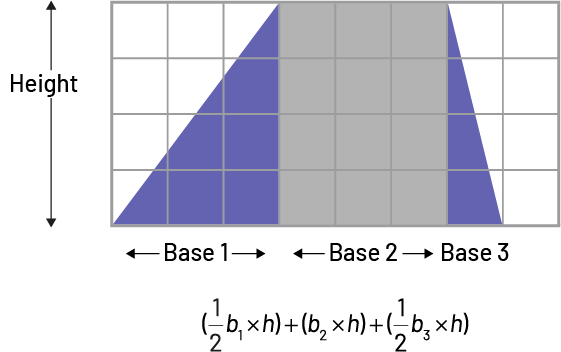Image there is a grid with eight columns and four rows. In the grid there is a trapeze that is divided in two triangles and one parallelogram. The height, of the figures is indicated by an arrow, first base. The base of the parallelogram is base two and the base of the second triangle, base three. Below the grid these is an equation: (opening parenthesis) a half “ b ” index one, multiplied by “ h ” (closing parenthesis), plus, (opening parenthesis) “ b ” index two, multiplied by “ h ” (closing parenthesis), plus (opening parenthesis) half “ b ” index three, multiplied by “ h ” (closing parenthesis).
- A trapezoid can be doubled to create a parallelogram whose area is then divided in two.
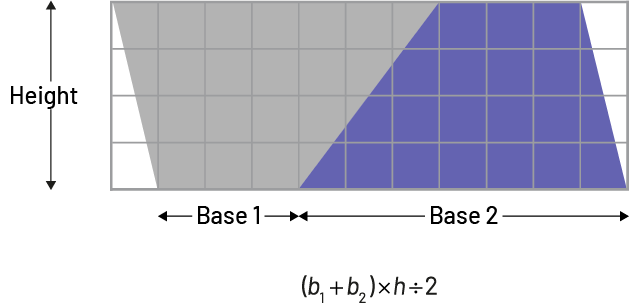Image there is a grid of eleven columns and four rows. In the grid, there is a trapeze which is doubled to form a parallelogram. This parallelogram is divided by its height, its base one and its base two. Below the grid, there is an equation: (opening parenthesis) “ b ” index one, plus “ b ” index two (closing parenthesis), multiplied by “ h ” divided by two.
- Two triangles can be added to a trapezoid to create a large rectangle from which their areas are then subtracted.
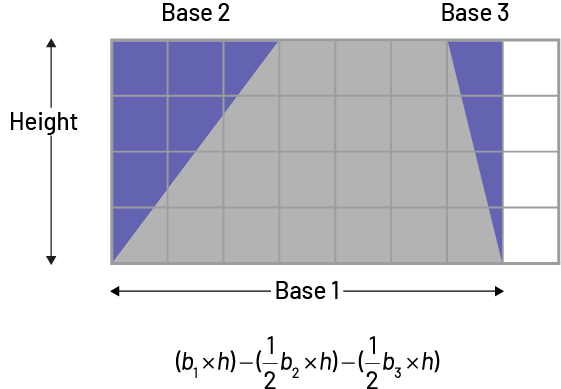Image There is a grid of eight columns and four rows. In the grid, there is a trapeze and two triangles, which form a rectangle. This quadrilateral is divided by its height, its base one and its base two. Below the grid, there is an equation:(opening parenthesis) “ b “ index one, multiplied by “ h ” (closing parenthesis), minus (opening parenthesis) one half “ b ” index two, multiplied by “ h “ (closing parenthesis), minus (opening parenthesis) one half “ b ” index three, multiplied by “ h ” (closing parenthesis).
- A trapezoid can be reconfigured to form a rectangle with the same area and whose base is the average of the two bases of the trapezoid by drawing a rectangle that shares the two parallel sides of the trapezoid but that bisects the hypotenuse of each of the two triangles, then reflecting the new (smaller) triangle over the bisection line).
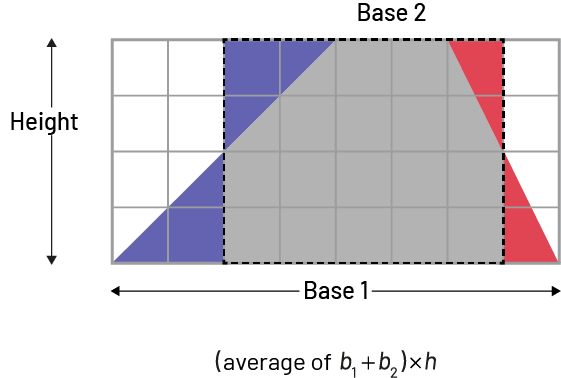Image There is a grid of eight columns and four rows. In the grid, there is a figure composed of a trapeze and four triangles. This parallelogram is divided by its height, its base one, its base two, and its base three. Below the grid, there is an equation: moyenne (opening parenthesis) “ b ” index one, plus “ b ” index two (closing parenthesis) multiplied by “ h ”.
The composition and decomposition strategies used to determine the area of a trapezoid can also be used to determine the area of a kite (decomposed into two triangles) and other complex polygons.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Complex Polygon
A complex polygon has an area composed of the area of several polygons.
