E1.1 Create lists of the geometric properties of various types of quadrilaterals, including the properties of the diagonals, rotational symmetry, and line symmetry.
Activity 1: Similar and Distinct Properties of Quadrilaterals
The lesson will take place in three distinct steps, namely:
Step 1: Before Learning (Warm-Up)
The teacher reviews the known quadrilaterals: square, rectangle, rhombus, parallelogram.
Step 2: Active Learning (Exploration)
The teacher introduces three new quadrilaterals (trapezoid, kite, and dart) and then asks students to classify the quadrilaterals according to certain properties.
Step 3: Consolidation of Learning
Students will notice that quadrilaterals have similarities and differences and that some have common properties.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 2: Is It Possible?
This activity integrates concepts of geometric and spatial reasoning, measurement, and probability.
The teacher makes a statement related to the properties of geometric shapes that present a certain, probable, or impossible situation. For example, the teacher says, “My pyramid has a square base.” Students must use their knowledge of the properties of geometric shapes to indicate whether it is certain, probable, or impossible that the teacher has this shape, and justifying their answer. In this example, a student could answer that it is probable because the pyramid could not only have a square base, but also a triangle, pentagon, hexagon, etc. base. The teacher then asks the students to modify the statement so that it represents a certain or impossible situation. For example, a student might say “my pyramid has a base” (a certain situation) or “my pyramid has no base” (an impossible situation).
Other statement examples:
- ”My hexagon has six sides.“ This statement presents a certainty, because all hexagons have six sides.
- ”My rectangle has a 45° angle.“ This statement presents an impossible situation, because all rectangles have four 90° angles.
- “My acute angle measures 120°”. This statement presents an impossible situation, because all acute angles measure less than 90°.
After grouping the students into pairs, the teacher asks them to write statements similar to the example they just worked through and that are related to geometric shapes they know. After each student has developed their statements, they will read them. The other student will specify, with justifications, whether the statement presents a definite, probable/possible, or impossible situation and then modify it so that it presents one of the other two situations. The student who reads the initial statement must in turn specify the situation that is presented by this new statement. The students will then switch roles.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 42.
Activity 3: My Puzzle
Using dynamic geometry software or applications, have students create a symmetrical rectangular puzzle using polygons of their choice. Ask them to then make a list of criteria that defines their puzzle. Once they have completed this task, have them exchange their list with another student and attempt to construct a puzzle that conforms to this list.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 1, p. 77.
Activity 4: Construction of Quadrilaterals Using Dynamic Geometry Software or Application
By conducting activities using technology, students are able to more easily create many cases quickly, allowing better analysis, testing of hypotheses, and making of conjectures. Using dynamic geometry software or applications enables students to more easily explore various cases within a class of geometric shapes. Students draw geometric shapes and can then move and transform them in many different ways. They can quickly construct and examine not only one geometric shape, but rather a large number of examples within a class of shapes. When a property of a geometric shape is preserved after a transformation, it is a characteristic of the geometric shape and is sufficient to describe an entire class of geometric shapes.
For example, the teacher can ask students to name different quadrilaterals that have diagonals that bisect each other. Using dynamic geometry software or an application, students can create an original quadrilateral with two vertices at the ends of a line segment and the other two vertices as points on a circle that shares its centre with the midpoint of the segment. The features of the software or application make it easy to measure lengths or angles. From these measurements, students can justify the number of different quadrilaterals that can be formed.
Here are examples of quadrilaterals obtained with dynamic geometry software:
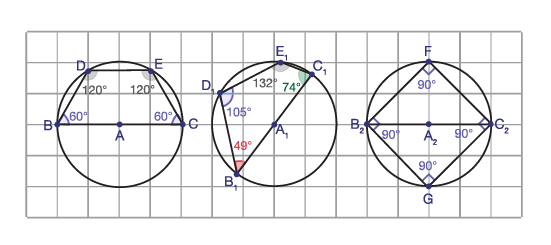Image this is a grid on which there are three circles. The is a quadrilateral is each individual circle: the first one has two angles of 120 degrees and two angles of 60 degrees; the second one has an angle of 105 degrees, an angle of 132 degrees, an angle of 74 degrees, and an angle of 49 degrees; the third one has three angles of 90 degrees.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, Mesure et géométrie, Fascicule 3, p. 27.
Activity 5: Quadrilaterals
Provide students with a set of quadrilaterals and ask them to draw them using dynamic geometry software or an application. Also provide them with the observation table or upload a document to a web platform so that they can record their observations.
Observation Table
|
Shape |
Name and Characteristics |
Number of Diagonals |
Side Midpoints |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 |
Step 1
Have students observe the quadrilaterals, determine their characteristics, and then complete the first column of the observation table.
Students should be able to identify the types of quadrilaterals (parallelogram, right trapezoid, isosceles trapezoid, square, rhombus, kite, any quadrilateral) and their characteristics (congruent sides, parallel sides, perpendicular sides, congruent angles).
Invite students to check whether their observations about one quadrilateral apply to other quadrilaterals. For example, ask them to:
- check if the same characteristics apply to other quadrilaterals;
- draw a quadrilateral that has four equal sides, but no right angles.
Step 2
At this stage in their learning, according to the criteria defined by Van Hiele, students should have a level of geometric reasoning of level 1, namely analysis. A sample activity could be: For each of the nine shapes, have students use technology to draw their diagonals and then record their observations in the third column of the table (for example, two diagonals; two diagonals that bisect each other).
The exploration of the diagonals of the quadrilaterals can also be done using strips of paper with holes (for example., dot matrix paper) and brass plated fasteners or plastic sticks (such as GeoStix). The strips of paper can be used to represent the diagonals and fixed with the fasteners. Thus, students can think about the properties and characteristics of the different geometric shapes. They can then group the quadrilaterals into classes, according to the properties of their diagonals, such as number of diagonals, whether the diagonals bisect each other, and the presence or absence of a 90 degree angle at their intersection.
Image There are four images. In the first one, here are two strips of holed paper in the shape of an “x”. In the second image, there are two plus symbols and two “x” symbols on a cartesian plane. In the third image, there are two plus symbols and one “x”. In the fourth image, there are three quadrilaterals marked by a plus symbol or an “x”.
Invite students to explore how and where the diagonals of different quadrilaterals intersect; for example:
- Are there several quadrilaterals whose diagonals bisect each other?
- Are there quadrilaterals whose diagonals bisect at a 90° angle?
Step 3
Ask students to join the midpoints of the sides of each given quadrilateral to form another quadrilateral and write their observations in the last column of the table.
Step 4
Using dynamic geometry software or applications, have students formulate hypotheses based on their observations, draw conclusions and generalize their conclusion.
In the example below, shape ABCD is a square and the inner shape is also a square or parallelogram. If vertex C is moved horizontally to the right, the resulting shape is a right-angled trapezoid and the inner shape is still a parallelogram.
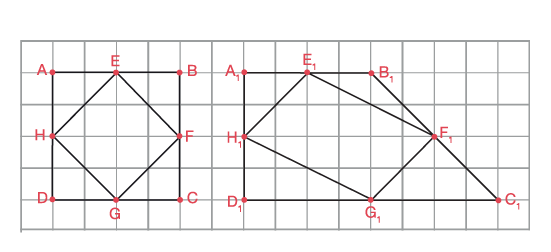Image The is a grid on which there are two sets of superimposed quadrilaterals. The peak of the second quadrilateral is longer than the one in the first set.
In the example below, shape ABCD is a parallelogram and shape HEFG is also a parallelogram. If vertex C is moved to the right and down, the resulting shape is a general quadrilateral and the inner shape is still a parallelogram.
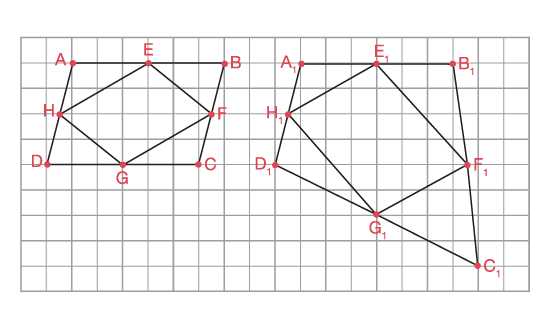Image a grid in which there are two sets of superimposed parallelograms. The peak of the second parallelogram is long than the one in the first set.
In the example below, shape ADFB is a concave quadrilateral and shape CEGH is a parallelogram. If vertex D is moved to the right and down, the resulting shape is another concave quadrilateral and the resulting inner shape is still a parallelogram.
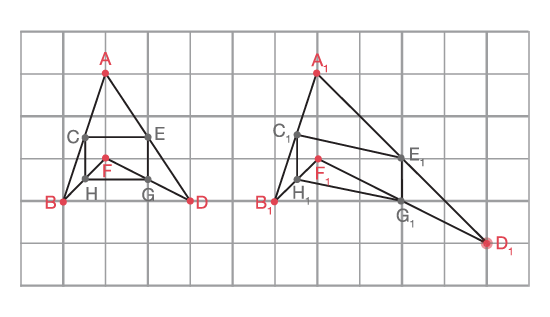Image A grid on which there are two sets of superimposed quadrilaterals. The peak of the second quadrilateral is longer than the one in the first set.
Invite students to explore different methods of proving the same hypothesis; for example:
- How can you show, using geometry, that if two diagonals of a quadrilateral bisect at their midpoints, then it is a parallelogram?
- How can you show, using geometry, that the shape that connects the midpoints of the sides of an isosceles trapezoid is always a parallelogram?
Source: translated from Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, Mesure et géométrie, Fascicule 3, p. 28-31.