E2.2 Use a protractor to measure and construct angles up to 360°, and state the relationship between angles that are measured clockwise and those that are measured counterclockwise.
Activity 1: Rolling Angles
How many degrees are between each spoke of the wheels of a bicycle with 36 spokes? 20 spokes? Explain your reasoning.
(The teacher might project a drawing of a bicycle wheel without spokes for recording student responses.)
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 2: Constructing Angles
Draw, on the plane below, two line segments, OA and OB, which form an angle of 235°.
Strategy 1
The 235° angle is a reflex angle (it is greater than 180°), and therefore greater than the straight (180°) angle shown. To draw this angle, I will use the addition of two angles: 235° = 180° + 55°.
Image there are two line segments. In the first quadrant, there is a point “ a ” from which an oblique line crosses the first and the third quadrant, passing by the point “ o ”.
I place my protractor so that the 0° line is on the straight line. I measure the angle of 55° which will complete my 235° angle.
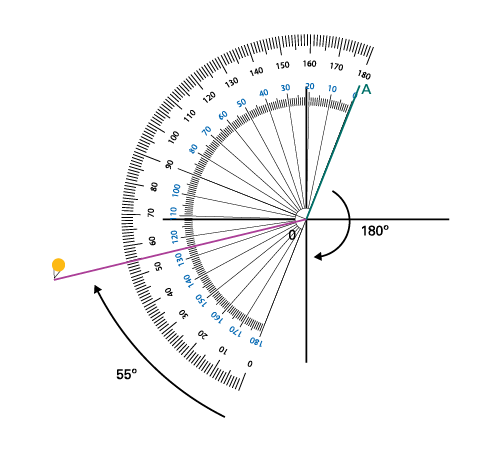Image there are two line segments. In the first quadrant, there is a point “ a ” from which an oblique line crosses the first and the third quadrant, passing by the point “ o ”. Above, there is a protractor which measures an angle of 55 degrees. Going from the line in the first quadrant, here is a curved arrow pointing towards the left in a clockwise motion. Next to this arrow is written: 180 degrees.
I can then place point B and draw the line segment OB.
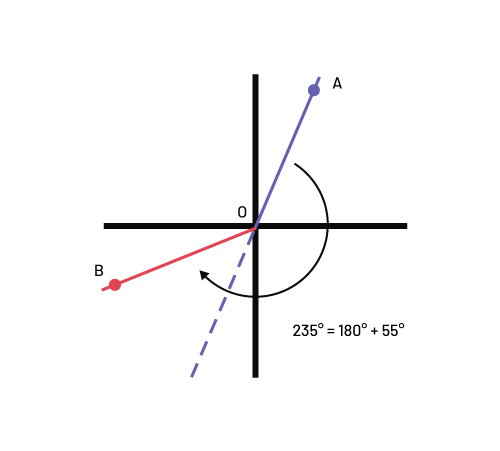Image there are two line segments. In the first quadrant, there is a point “ a “ from which an oblique line crosses the first and the third quadrant, passing by the point “ o “. A second starts from the point “ b “ and stops at the point “ o “. In the corner is written: 235 degrees equals 180 degrees plus 55 degrees.
Strategy 2
Since 235° is larger than 180°, I know I need to draw a reflex angle. I can think about this as removing a piece from a full angle (360°). I draw the line segment OA, so from this I will read the measurement counterclockwise on my protractor.
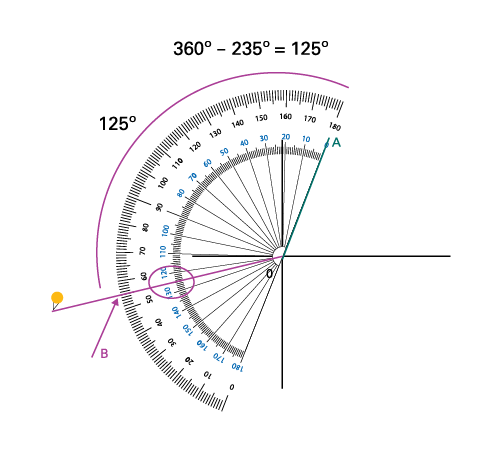Image There are two line segments. In the first quadrant, there is a point “ a ” from which an oblique line crosses the first and the third quadrant, passing by the point “ o ”. Above, there is a protractor which measures an angle of 125 degrees from the line “ a “ to the line “ b ”. Above is written: 360 degrees minus 235 degrees equals 125 degrees.
Since 235° = 360° - 125°, I can measure an angle of 125°, place point B, and draw the segment OB. Then angle AOB will be 235°.
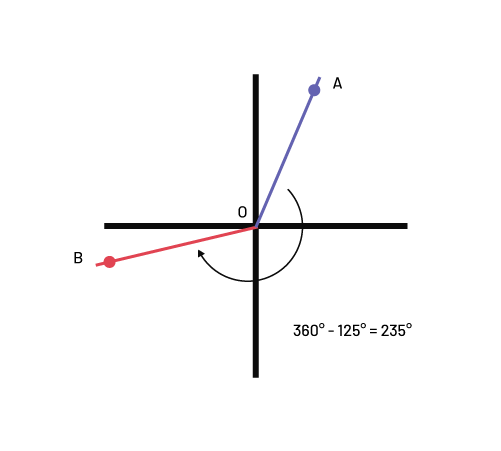Image there are two line segments. In the first quadrant, there is a point “ a “ in the first quadrant which stops a the point “ o “. In the corner is written: 360 degrees minus 125 degrees equals 235 degrees.
Source: translated from En avant les maths!, 6e année, CM, Sens de l’espace, p. 11-13.