E2.4 Determine the areas of trapezoids, rhombuses, kites, and composite polygons by decomposing them into shapes with known areas.
Activity 1: Generalization Activities for Area – Shapes with a Given Area
Goal
In this activity, students will consolidate their understanding of measuring the area of a surface.
Material
- Geoboard 11 by 11 (one per student)
- Appendix 4 (1 cm x 1 cm grid)
- Appendix 5 (Geoboard paper)
- ruler graduated in centimetres
Instructions
Using a Geoboard, grid or ruler, construct each of the shapes below with a given area. Reproduce the shapes in your notebook.
- A rectangle with an area of 20 square units.
- A square with an area of 36 square units.
- A parallelogram with an area of 16 square units.
- A triangle with an area of 24 square units.
- A trapezoid with an area of 15 square units.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 2: Relationships Between Various Area Formulas
This activity focuses on determining formulas and establishing relationships between various area formulas.
Ask students to determine the area of a trapezoid.

Student 1 visualizes the trapezoid as a rectangle and two triangles.
Student 2 visualizes the trapezoid as a parallelogram and a triangle.
Student 3 visualizes the trapezoid as two triangles.
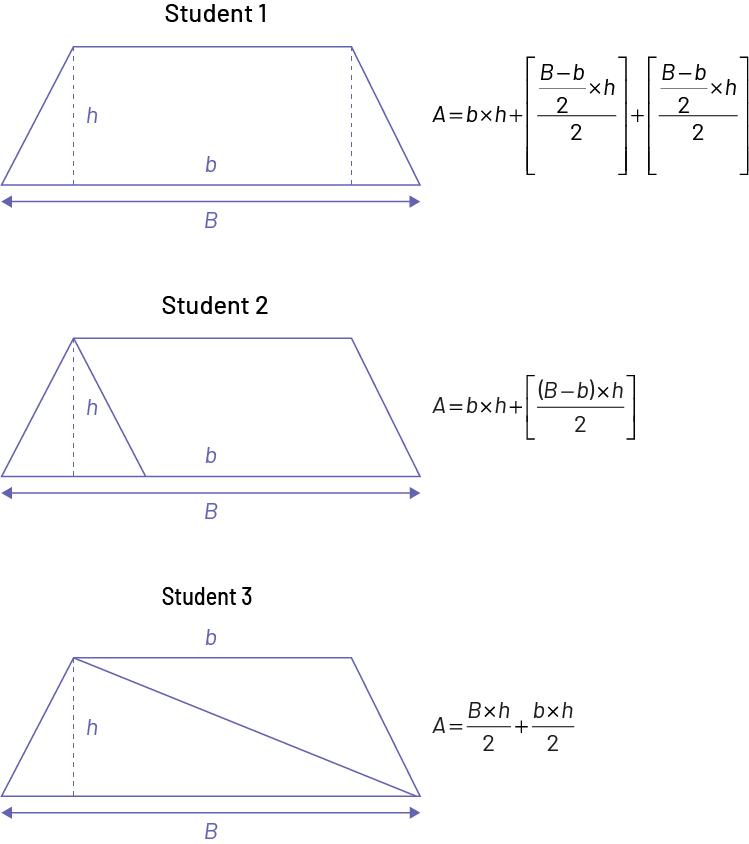
Image Student one: A trapeze, of which the base is named uppercase “ b ”, is divided in three parts. Two dotted lines are traced, representing height “ h ”; which forms two triangles. The rectangle at the base of the triangle has a width “ h ” and a length “ b ”. “ A ” equals, “ b ” multiplied by “ h ”, plus [opening bracket] “ B ” minus “ b ”, divided by two, multiplied by “ h ”, divided by two [closing backet] plus, [opening bracket] “ B ” minus “ b ” divided by, two multiplied by “ H ”, divided by two [closing bracket]. image Student two: A trapeze, of which the base is named uppercase “ b ”, is divided in two parts, being an equilateral triangle and a parallelogram. The height of the triangle is H ” and the base of the parallelogram is “ b ”. “ A ” equals, “ b ” multiplied by, “ H ” plus [opening bracket] (opening parenthesis) “ B ” minus “ b ” (closing parenthesis) multiplied by “ h ”, divided by two [closing brackets]. image Student three: A trapeze whose base is named uppercase “ B ”, is divided in two parts. Two scalene triangles. The height of the first triangle is “ h ”, and the base of the second triangle is “ b ”. “ A ” equals “ b ” multiplied by “ h ”, divided by two plus “ B ” multiplied by “ H ”, divided by two.
During the consolidation of learning, compare the equations the students have written, then come up with one formula to calculate the area of a trapezoid. Facilitate a class discussion about the effectiveness of the solutions presented.
Verify with students the correctness of the formula obtained by calculating the area of other trapezoids oriented in various ways (base longer at the top, right angle, non-symmetric angle, etcetera)

Skills to be developed related to spatial visualization:
- Perception of spatial relationships
- Mental rotation
Source: translated from Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, Mesure et géométrie, Fascicule 3, p. 15-17.
