GEEM - Learning Situation

E2. Measurement

Compare, estimate and determine measurements in various contexts.

Learning Situation 1: How Much Space Does This Prism Occupy?

Total Duration: approximately 90 minutes

Summary

In this learning situation, students construct rectangle-based prisms from nets. Students then estimate and determine the volume of these prisms using unit cubes, and they explain the strategy used in each case.

Learning Goals

The purpose of this learning situation is to have students:

recognize certain measurable attributes of an object;
understand what the volume attribute means;
estimate and determine the volume of a rectangle-based prism using unit cubes;
explore the concepts of iteration, conservation, transitivity, additivity, and the structure associated with metric units.

Learning Context	Prerequisites
In Grade 7, students explore volume of a three-dimensional object using unit cubes. To avoid confusing capacity and volume, it is preferable to use closed three-dimensional objects for this activity.	This learning situation supports students to understand that the volume of an object corresponds to the size of the space it occupies, that this size is expressed in cubic units and that one way to determine this volume is to reproduce the object using unit cubes.

To be able to complete this learning situation, students must be able to:

recognize various measurable attributes of an object;
build a prism from its net;
construct, using unit cubes, a prism that has the same dimensions as a given prism.

Materials

closed rectangle-based prism boxes (two)
Appendix 4.1 (one copy per team of four)
scissors (one pair per student)
tape (one roll per team of four)
bags of approximately 150 individual cubes (one bag per team of four)

Mathematics Vocabulary

measurable attribute, area, face, perimeter, length, width, volume, mass, capacity, unit cubes, array

Before Learning (Warm-Up)

Duration: approximately 15 minutes

Present students with two closed boxes that are rectangle-based prisms. Ask them to identify as many measurable attributes of these prisms as possible and record them in their math journal.

A teacher presents 2 closed boxes in the shape of a rectangular prism.

Then ask a few students to name one of the attributes they have determined (for example, length, height, width, thickness, area of a face, perimeter of a face, mass) and to explain what this attribute represents by illustrating it using one of the prisms.

Examples

A student examines the box in the shape of a rectangular prism

Here is the length of this face of the prism.

Students measure a box in the shape of a rectangular prism.

The length of the string represents the perimeter of the front or back face of the prism.

Ask students to identify which prism they think takes up the most space and justify their answer. For example, some students might say that one prism takes up the most space because it is longer, while others might say that the other prism takes up the most space because it is thicker. Then ask, “How could we determine how much space each of these prisms takes up?”.

Possible Answer	Possible Interventions
We can measure the height.	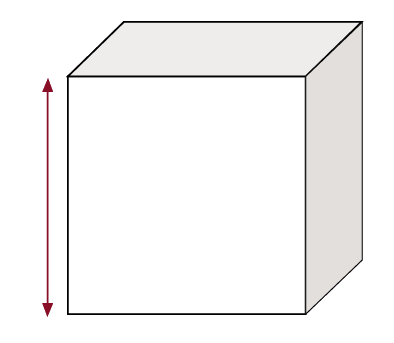Ask other students what they think. Support students to recognize that another prism could be the same height, but occupy a larger or smaller space.
We can find the area of each face and add them up.	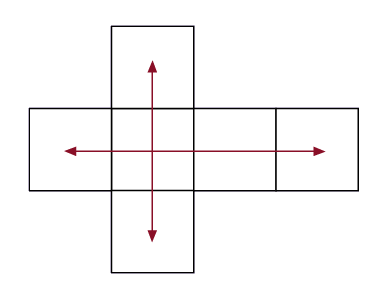Ask the other students what they think. Support students to recognize that the sum of the areas of the faces represents the surface area of the prism, or the measure of the two-dimensional space that the prism faces occupy.
It can be reproduced with cubes.	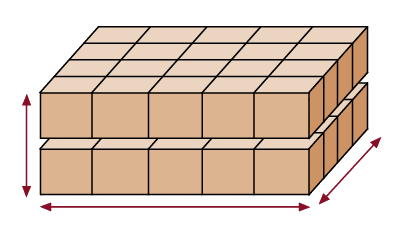Ask the other students what they think about this. Support students to recognize that this concrete model represents the measure of the three-dimensional space that the prism occupies and the count of cubes corresponds to the volume.

Active Learning (Exploration)

Duration: approximately 45 minutes

Tell students that the size of the three-dimensional space that an object occupies is called the volume.

Form teams of four and have students explore the concept of volume further. Give each team a copy of Appendix 4.1 (Prism Nets). Have them cut out each of the nets, construct the corresponding prisms, and place them in ascending order according to their estimate of volumes.

Then ask a few teams to present their answer and explain the strategy used to compare volumes.

Example

One team presents the prisms placed as in the picture below and provides the following explanation: “Prism D occupies the smallest space. Prisms A and B have the same volume. To find this, we placed the prisms back-to-back and compared them.”.

Facilitate a discussion about the different answers offered and highlight the importance of finding a more effective way to compare volumes. Give a unit cube to each team and ask them to use it to estimate the volume of the prisms.

Note: The results presented below reflect the volume if a 1 cm³ is used, although other cubes could be used (for example, unit cubes with 2 cm edges) and the measurements modified accordingly.

Circulate and let students decide how to use the unit cube to determine the volume of each prism. Students can, for example, mentally place the cube in an orderly fashion at various locations along a prism and estimate the number of times they need to place it to fill the entire space occupied by that prism.

When all the teams have finished, ask a few to present their results and describe the strategy used. Encourage them to place the prisms in ascending order of volume and compare this result with the previous result.

Example

A team presents their result using a table and provides the following explanation: “We estimated the number of cubes it would take to occupy the same space as the prism. We then placed the prisms in ascending order of volume and found that this ranking was different from what we thought when we did our first estimate. “

Prism	Number of Cubes
D	18
A	20
B	24
C	32

After the presentations, give each team a bag containing approximately 150-unit cubes and ask them to determine the exact volume of each prism by reproducing them using these cubes. Circulate and provide support as needed.

Possible Observation	Possible Interventions
One team decides to cover prism A with cubes.	Support students to realize that the prism they are building is larger than Prism A. Point out that the volume of Prism A is actually the interior volume of the prism they are building.
One team builds a rectangular arrangement larger than the base of prism B.	Have the team construct a prism by superimposing rectangular arrangements of this size, then compare it to Prism B. Support students to realize that the prism built with the cubes is wider and longer than Prism B. Point out that the top face of the rectangular arrangement must have the same area as the base of Prism B.
The team opens prism D and tries to fill it.	Suport students to realize that what they are measuring is not the volume of Prism D, but its capacity. To help them understand the difference, invite them to imagine that the prism is made of polystyrene 1 cm thick.

Consolidation of Learning

Duration: approximately 30 minutes

Group students together and ask the following questions:

What do you notice about the volume of the prisms? (All prisms have a volume of 24 cubes)
How does this result compare with the two previous estimates? (This is not the same, as we thought the volumes were all different, that prism C had a larger volume than prism B…)

Then invite a few teams to describe the strategy used to determine the volume of the prisms.

Example 1

Team members report that they have replicated each prism using cubes and counted the cubes used in each case.

Prisms built with interlocking cubes, and others in paper. They are organized in similar pairs.

Example 2

Members of a second team say they used a different strategy and explain it as follows: “We covered the top of Prism C with cubes and made an array of 12 cubes. We then superimposed a second array and obtained a volume equal to the volume of Prism C. We saw that the volume of Prism C is equal to 24 cubes, which is the same as two rectangular layouts containing 12 cubes each. ”

A student works with paper prisms and interlocking cube prisms.

Example 3

A third team explains the strategy used as follows: “We did something very similar to the second team to find the volume of Prism B. We first constructed an array the size of one of the ends of the prism. We then added identical arrays until we had a prism of the same volume as the original prism. Since we had six arrays and each was made up of four cubes, we determined that the volume of Prism B is equal to 24 cubes. ”

A paper prism is compared with a prism made of interlocking cubes.

Point out to students that they used different strategies to determine that the volume of each prism is equal to 24 cubes. Now ask them to explain how they could show that the four prisms have the same volume, without counting the cubes. Model, if necessary, how to decompose one of the four prisms to form one of the other three prisms.

Examples

The volume of Prism A is the same as that of Prism B, because if we decompose Prism A into two identical prisms and superimpose them, we can make Prism B.

Two paper prisms are compared with two nesting cube prisms.

Prisms C and D have the same volume, because if we separate the two rectangular arrangements which are superimposed to form Prism C and place them next to each other, we obtain Prism D.

The volume of Prism C is equal to the volume of Prism B, because if we split Prism C into two identical prisms and place them end to end, we get Prism B.

Two figures consist of the same number of cubes and of the same shape have a different orientation.

Take the opportunity to explore with students the concept of conservation of volume. Also explore the concept of transitivity by pointing out, for example, that if we show that the volume of Prism A is equal to the volume of Prism B and that the volume of Prism B is equal to the volume of Prism C, then it is possible to conclude that the volume of Prism A is equal to the volume of Prism C.

Differentiated Instruction

To Facilitate the Task	To Enrich the Task
Give the students four rectangle-based prisms made up of 24 interlocking cubes, instead of the nets of prisms in Appendix 4.1, and ask them to compare the volumes by using the cubes of one of the prisms to reproduce each of the other three.	Ask students to identify and construct rectangle-based prisms, other than Prisms A, B, C, and D, that have a volume of 24 cubes. (There are two possible prisms. Their dimensions are: 1 by 1 by 24 and 1 by 3 by 8.)

Follow-up at Home

Have students choose three boxes that are rectangle-based prisms (for example, cereal box, cookie box, shoe box) and determine a way to place them in order of increasing volume.

Additional Activity 1: Mr. Edifico's Village

Present the following situation to the students.

Mr. Edifico loves to build miniature villages around his electric train, so he decided to build a village made up of 12 buildings of different shapes but the same size.

Can you come up with 12 different models of buildings that he could build? Because of the size of the miniature village, your buildings must all have the same volume of 7, 8, 9 or 10 cubes.

Note: The two buildings shown below have a volume of 5 cubes. However, they are not different since they have the same shape. It is only the orientation of the different parts that has changed, not the shape.

Form teams of three and give each team a bag of approximately 150 interlocking cubes. Allow enough time for them to build various structures.

Circulate and provide support as needed. For example, if a team builds a structure in which two cubes have a common edge rather than a common face, point out that these are two buildings, not one.

Two figures made of interlocking cubes. The two figures touch each other by an edge.

When all teams have finished, ask a few to present their village. Invite other students to ask questions and share their observations.

Facilitate the exchange by asking questions such as:

Are all buildings shaped differently? How do you know?
Do all buildings have the same volume? Justify your answer.

Extension

Ask students to compare the buildings according to:

the number of vertices, edges or faces;
the perimeter or area of their base.

Note: This activity can be done using a digital tool or application related to building structures (for example, Minecraft)

Source: translated from Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 127-138.

Learning Situation 2: Happy as a Clam

Total Duration: approximately 130 minutes

Summary

In this learning situation, students explore the relationship between millilitres (mL) and cubic centimetres (cm³) by determining the volume of regular and irregular three-dimensional objects using the displacement of water.

Learning Goals

The purpose of this learning situation is to have students:

develop their measurement skills;
recognize that the volume of an object is the size of the three-dimensional space it occupies;
relate the volume of an object to the volume of water it displaces when immersed;
discover the equivalence relationship between millilitres (mL) and cubic centimeters (cm³);
consolidate their understanding of the concept of conservation of volume.

Learning Context

Prerequisites

In previous years, students have learned to determine the capacity of containers using appropriate metric units.

In Grade 7, students need to understand the difference between capacity and volume. For example, a bottle may have a capacity of 350 mL of juice, but only contain a volume of 300 mL of juice; a closed wooden box may have an external volume of 1 m³, but a capacity of 0.9 m³. Students also need to explore the relationship between the volume of an object, in cubic centimetres, and the volume of liquid, in millilitres. For example, when an object with a volume of 1 cm³ is immersed in water, it displaces a volume of water equivalent to 1 mL.

This learning situation allows students to develop a better understanding of the volume attribute and to discover the equivalence relationship between cubic centimetres and millilitres, that is 1 cm³ = 1 mL.

To be able to complete this learning situation, students must:

know the metric units for volume, namely, cubic centimetres (cm³) and millilitres (mL);
be able to estimate and measure the volume of regular three-dimensional objects, using different strategies. For example, count the cubes needed to reproduce the object, count the cubes needed to construct a rectangular array that covers the base of the object and multiply that by the number of arrays needed to build the three-dimensional object, use a formula.

Materials

different prisms, made with modeling clay, with a volume greater than or equal to 30 cm³ (one per team)
Appendix 6.1 (one worksheet per team)
Appendix 6.2 (one worksheet per team)
1 cm³ cubes
sheets of centimetre grid paper
string
rulers
graduated containers of 250 mL or more (one per team)
50 mL or less graduated test tubes (one per team)
funnels (one per team)
water containers
trays (one per team)
large sheets of paper (two per team)

Mathematics Vocabulary

measurable attribute, volume, cubic centimetre (cm³), millilitre (mL), rectangle-based prism, regular three-dimensional object, irregular three-dimensional object

Note: This learning situation consists of two Exploration sections, each followed by a Consolidation of Learning. The purpose of this organization is to facilitate time management and to allow students to gradually build on the concepts being addressed.

Before Learning (Warm-Up)

Duration: 20 minutes

Present students with a block of modeling clay and ask them to list measurable attributes of this prism (for example, length, width, height, volume, perimeter, mass).

Facilitate a discussion by asking questions such as:

How can you measure each of these attributes? (For example, length, width and perimeter can be measured with a ruler, mass with a balance, volume with cubes.)
What is the volume of a three-dimensional object? (It is the measure of the space it occupies.)
Why would one want to know the volume of a three-dimensional object? (for example, to find a box it can fit in, to find a place it can fit on a shelf…)
What standard metric units are usually used to determine the volume of a three-dimensional object? (Cubic units such as cubic centimetres or cubic metres are used.)
What standard metric units are usually used to determine the volume of a given amount of liquid? (Units such as millilitres or litres are used.)

Make different rectangle-based prisms in advance using modeling clay. Make sure that the volume of each prism is at least 30 cm³. Form teams. Distribute a prism to each team and a worksheet (see Appendix 6.1).

Ask students to estimate the volume of their prism and record this estimation in the first column of the worksheet.

Modeling clay blocks: blue, yellow, red and green.

Construct a group chart (see Appendix 6.2) on a large sheet of paper, an interactive whiteboard, an overhead, or on the board, and record each team's estimations.

Example

Team	Estimation of the Prism's Volume	Measurement of the Prism's Volume	Estimation of the Volume of Water Displaced by the Prism	Measurement of the Volume of Water Displaced by the Prism	Estimation of the Volume of Water Displaced by the Fish	Measurement of the Volume of Water Displaced by the Fish
M and J	30 cm³
C and Y	45 cm³
E and D	82 cm³
P and S	56 cm³

Then have students determine the volume of their prism using a strategy of their choice (for example, replicate the prism using 1 cm³cubes, apply a formula) and record this result in the second column of their worksheet. Provide them with the necessary materials (for example, 1 cm³cubes, sheets of cm²grid paper, string, rulers). Then have them compare the measurement of the volume of their prism with their estimation.

A student measures one side of a modeling clay prism.

Lead a brief discussion about the different strategies used to determine the volume of the prisms, and then record the volume of each team's prism in the group chart.

Example

Team	Estimation of the Prism's Volume	Measurement of the Prism's Volume	Estimation of the Volume of Water Displaced by the Prism	Measurement of the Volume of Water Displaced by the Prism	Estimation of the Volume of Water Displaced by the Fish	Measurement of the Volume of Water Displaced by the Fish
M and J	30 cm³	36 cm³
C and Y	45 cm³	48 cm³
E and D	82 cm³	72 cm³
P and S	56 cm³	60 cm³

Next, encourage students to think about the idea of using water displacement as a strategy for measuring the volume of an object by asking questions such as:

If you dip your prism into a container of water, what effect will it have on the water level in the container? (The water level will rise.)
Why will the water be displaced in this way? (The water is displaced because the prism takes up space in the container.)

Then ask students to estimate the volume of water their prism will move after it is immersed in water and record this estimation in the third column of their worksheet. Then have them perform an experiment to verify their estimation.

Active Learning (Exploration) - 1

Duration: 40 minutes

Distribute to each team a graduated container (for example, test tube, beaker) of 250 mL or more in which it is possible to immerse their prism, a test tube of 50 mL or less, a funnel, a container of water and a tray. Ask them to place all the materials on the tray.

Students doing an experiment. They have as equipment: a funnel, water, a graduated cylinder, a tray.

Ask students to use this material to determine the volume of water displaced when they immerse their prism, record this result in the fourth column of their worksheet, and describe, on a large sheet of paper, the strategy they used.

Allow sufficient time for all teams to complete the experiment. Circulate, observe the strategies used, and provide support as needed. The table below provides two examples of such teacher moves.

Possible Observations

Possible Interventions

Students fill the graduated cylinder to the brim, dip the prism in, and then remove it. They then read the volume of water remaining in the graduated cylinder and record this measurement as the volume of water displaced by the prism.

Get students to think about the noted measurement by asking questions such as:

What did you want to find by doing this experiment? (The volume of water displaced by the prism.)
Where is the water displaced by the prism? (In the tray.)
Does the measurement you wrote down correspond to the volume of water displaced? (No, it corresponds instead to the volume of water remaining in the graduated cylinder after the prism is immersed in it.)
What should you measure? (The volume of water in the tray)
How would you go about measuring this volume of water? (We could pour this water into the test tube and read the volume measurement.)

Students fill the graduated cylinder to the brim, dip the prism in, and then remove it. They then seem unable to determine the volume of water displaced.

Encourage students to find the source of their difficulties by asking questions such as:

Tell me a little bit about what you are doing here. (We want to calculate the difference between the volume of water before and after we added the cube.)
This is a good strategy. Why do you have a problem with this strategy? (The cylinder is not graduated all the way to the top. So we don't know the volume of water that was displaced.)
What could you do to determine this? (We could start by putting water up to the line that says 250 mL. We could then put 50 mL of water in the small test tube and pour this water into the graduated cylinder until it is full. By determining the volume of water added, one could calculate the volume of water to start with.)

Consolidation of Learning - 1

Duration: 30 minutes

Note: This consolidation is done in two stages. First, the strategies used to determine the volume of water moved are shared, highlighting the variety of possible strategies and the importance of measuring accurately in order to account for the meniscus. Next, the volumes obtained are shared, encouraging students to look for a relationship between millilitres and cubic centimetres.

Invite a few teams to explain the strategy they used to determine the volume of water displaced by the prism. Select teams that used different strategies. After each presentation, invite other students to ask questions if necessary, and discuss the advantages and disadvantages of the strategy used (for example, difficult to retrieve all the water that overflowed from the graduated cylinder).

Some of the strategies that students could use include:

Students fill the graduated cylinder to the brim, immerse the prism in it, and then remove it. To determine the volume of water displaced by the prism, they put 1 cm³ cubes into the cylinder to fill it to the brim again. They record the number of cubes put into the cylinder as a measurement of the volume of water displaced.
Students fill the graduated cylinder to the brim and dip the prism into it, causing the water to overflow. They then empty all of the overflowing water into the testing tube and take a reading of the water level (for example, 45 mL) to obtain the volume of water displaced by the prism.
Students fill the graduated cylinder to a certain level and record the volume of water (for example, 100 mL). They then immerse the prism in the water and record the level of the water (for example, 140 mL). To determine the volume of water displaced by the prism, students calculate the difference between the water levels before and after the prism was immersed (140 mL - 100 mL = 40 mL).

A graduated cylinder. It contains a quantity of liquid.

Students place the prism in the graduated cylinder, cover it with water and take a water level reading (for example, 175 mL). They then remove the prism and read the water level again (for example, 125 mL). To determine the volume of water displaced, students calculate the difference between these two levels (175 mL - 125 mL = 50 mL).

Once the presentations of the strategies are concluded, invite one member of each team to record in the group chart the measurement obtained for the volume of water moved by their prism.

Example

Team	Estimation of the Prism's Volume	Measurement of the Prism's Volume	Estimation of the Volume of Water Displaced by the Prism	Measurement of the Volume of Water Displaced by the Prism	Estimation of the Volume of Water Displaced by the Fish	Measurement of the Volume of Water Displaced by the Fish
M and J	30 cm³	36 cm³	40 mL	37 mL
C and Y	45 cm³	48 cm³	62 mL	50 mL
E and D	82 cm³	72 cm³	50 mL	71 mL
P and S	56 cm³	60 cm³	62 mL	60 mL

Encourage students to relate the volume of the prism (third column of the group chart) to the volume of water displaced (fifth column of the group chart) by asking questions such as:

If you compare the measurement of your prism's volume with the measurement of the volume of water displaced by the prism, what do you observe? (The number of units for the prism's volume and the number of units for the volume of water displaced are almost the same.)
What conjecture could you make based on the results of this experiment? (The volume of water displaced by an object immersed in water is equivalent to the volume of the object.)
In several cases, the measurement of the prism's volume is not exactly equal to the measurement of the volume of water displaced. How might these differences be explained? (They may be the result of a calculation error or difficulties in the way the experiment was performed and measured.)
Would the volume of water displaced by your prism be the same if you used a different container? Why? (It would be the same since the volume of water displaced depends on the prism's volume and not the capacity of the container in which it is immersed.)
What metric unit is used to determine the prism's volume? (The cubic centimetre.)
What metric unit is used to determine the volume of water displaced? (The millilitre.)
What relationship seems to exist between these two units? (An object of 1 cm³ displaces 1 mL of water.)

Once students have established the relationship between cubic centimetres and millilitres, have them use this relationship to determine the volume of an irregular three-dimensional object.

Active Learning (Exploration) - 2

Duration: 20 minutes

Invite students to form the same teams as before. Ask them to create a model of a fish from their clay prism. Point out that they must use all the clay and make sure that the fish can fit completely into the measuring cup.

Then ask students to determine the volume, in cubic centimetres, of the fish using the following procedure.

Estimate the volume of water the fish will displace when submerged and record this estimation in the fifth column of the worksheet;
Use the strategy of your choice to measure the volume of water displaced when the fish is immersed in water and record this result in the sixth column of the worksheet;
On a large sheet of paper, write the volume of your fish in cubic centimetres and indicate how you arrived at this result.

Make other irregular three-dimensional objects available to students who wish to verify their conclusion. Circulate, observe strategies used and provide support as needed.

Consolidation of Learning - 2

Duration: 20 minutes

Invite one member of each team to record their estimation and measurement of the volume of water displaced by their fish on the group chart.

Example

Team	Estimation of the Prism's Volume	Measurement of the Prism's Volume	Estimation of the Volume of Water Displaced by the Prism	Measurement of the Volume of Water Displaced by the Prism	Estimation of the Volume of Water Displaced by the Fish	Measurement of the Volume of Water Displaced by the Fish
M and J	30 cm³	36 cm³	40 mL	37 mL	35 mL	36 mL
C and Y	45 cm³	48 cm³	62 mL	50 mL	50 mL	49 mL
E and D	82 cm³	72 cm³	50 mL	71 mL	70 mL	70 mL
P and S	56 cm³	60 cm³	62 mL	60 mL	64 mL	60 mL

Invite a few teams to present and justify their results. For example, a team might say, “Our fish displaced 29 mL of water. In the first experiment, we saw that the volume in millilitres of water displaced by an immersed object is equivalent to the volume in cubic centimetres of the object. Therefore, we can conclude that the volume of our fish is equal to 29 cm³.”

Use the situation to encourage students to relate the results of the two experiments to the concept of conservation of volume by asking questions such as:

Is there a relationship between the volume of your fish and the volume of the original prism in the third column of the group chart? Why? (The volume of the fish is the same as the volume of the prism because both shapes are made from the same amount of clay.)
If you had shaped your clay prism into a seahorse instead of a fish, how much water would have been displaced? Justify your answer. (The volume of water displaced would have been the same because the size of the space occupied by the clay remains the same no matter what shape you give it.)
I made a starfish out of playdough. I want to determine its volume, but I don't have a measuring cup and water available. How could I determine the volume? (You could turn the starfish into a rectangle-based prism, then measure the dimensions of the prism and determine its volume. Since the starfish and the prism are made from the same amount of playdough, the two three-dimensional objects have the same volume.)

Differentiated Instruction

To Facilitate the Task	To Enrich the Task
During the warm-up, ask students to build a prism using 1 cm³ cubes instead of modeling clay (this will make it easier for them to determine the volume of the prism). In the second exploration, instead of turning the clay prism into a fish, they can make an irregular object using all the cubes that make up their prism.	Ask students to describe a procedure that would determine the volume of water displaced by an object placed in an ungraduated container (see example below).

Example

Poster made by students on the steps to find the volume of a fish.

Follow-up at Home

At home, students can take two objects that appear to have roughly the same volume (for example, a rock and a figurine) and ask a family member to indicate which object appears to have the greater volume. Then, using a measuring cup large enough to submerge the objects, they can verify this estimate by measuring the volume of water displaced by each object.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, Mesure, p. 157-168.

Overall Expectation	Specific Expectation
E2. Compare, estimate, and determine measurements in a variety of contexts.	E2.1 describe the difference and similarity between volume and capacity, and apply the relationship between millilitres (mL) and cubic centimetres (cm³) to solve problems.

Overall Expectation	Specific Expectation
E2. Compare, estimate, and determine measurements in a variety of contexts.	E2.1 Describe the differences and similarities between volume and capacity, and apply the relationship between millilitres (mL) and cubic centimetres (cm³) to solve problems.