E1.2 Draw top, front, and side views, as well as perspective views, of objects and physical spaces, using appropriate scales.
Skill: Drawing Views and Various Perspectives of Objects and Physical Spaces, According to Appropriate Scales
Three-dimensional objects can be represented using two dimensional views. Two-dimensional representations can show how objects are composed, how they can be navigated, or how they can be reproduced, and can be used to represent anything from very small to very large. They are used by designers, builders, urban planners, instruction illustrators, and others.
Top (plan) views, and front and side (elevation) views are “flat drawings” without perspective. They are used in technical drawings to ensure a faithful reproduction in three dimensions.
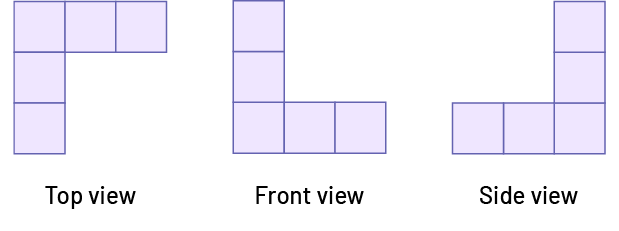image Top view: 5 blocks are placed to form an upside down « L » . Front view: 5 blocks are placed to form an « L ». Side view: 5 blocks are placed so as to form an « L » whose opening is to the right.
Scales are used to convey the proportions of the original (namely, angles and relative distances). If the scale is 1:100, then 1 cm represents 100 cm at full size, regardless of the view. A legend communicates the scale.
Two types of perspective drawings are isometric projections and cabinet projections. These drawings show three views (top, front, and side) in one illustration, but not the back view, so some elements of the object may be missing. They are also better at representing straight edges than curves and to achieve the appearance of perspective, they may distort angles and lengths.
Isometric dot paper is useful for drawing isometric and cabinet projections, although the scale will be slightly distorted. To give the effect of perspective on this type of paper, the isometric projection slides each vertex by the same translation vector (for example, 5 to the right, 1 up), and the cabinet projection slides the front face by the same translation vector (for example, 5 to the right, 1 up) and joins the vertices.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Strategies for Drawing Different Views of a Three-Dimensional Object
Example 1
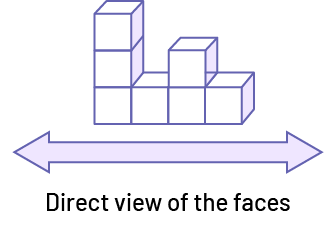
The student is asked to draw the front view, side view, and top view of the three-dimensional object below, using a 1:1 scale. The arrow indicates the front view of the three-dimensional object.
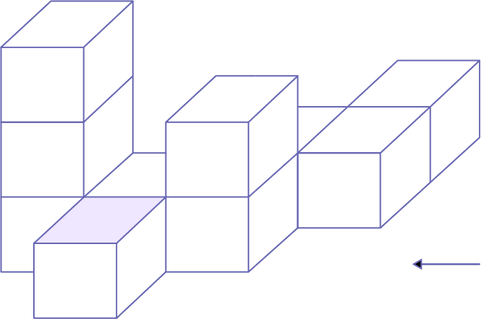
STRATEGY
Draw Front, Side and Top Views Using Appropriate Scales
To represent the three-dimensional object using interlocking cubes, the student might choose to reproduce the model using centimetre cubes. To represent the object to scale, the student could use cm grid paper, or use a ruler to draw the appropriate side lengths.
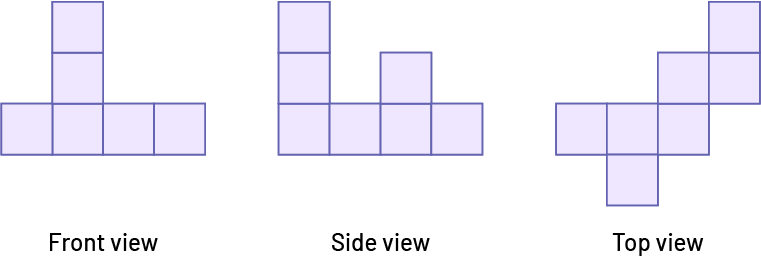
Example 2
The student must carefully observe this three-dimensional object and represent it by making two perspective drawings: the isometric projection and the cabinet projection.
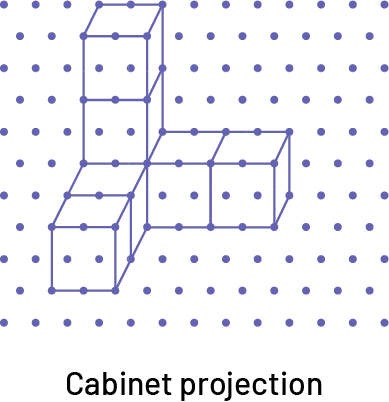
Isometric Projection
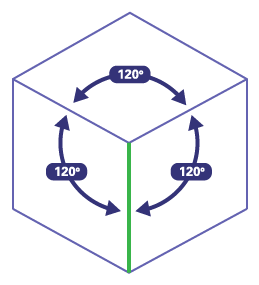
To represent the three dimensions of the three-dimensional object using an isometric projection, the student should use isometric dot paper. This paper is made with vertical and oblique (diagonal) straight lines that form 120° angles and is very useful for drawing the edges of the three-dimensional object.
An isometric projection represents an object in perspective from a “corner view”. The student draws the object so that the edges (height, width, depth) form angles of 120°and represents an edge in the foreground.
Each dimension of the object is represented on a constant scale and the student can use a 1:2 scale to draw the object, such that 1 cm on the drawing represents 2 cm of the object.
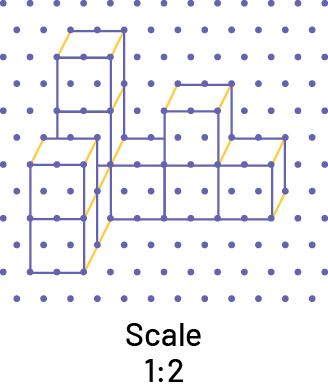
Cabinet Projection
The cabinet projection shows an object from “straight on” with the depth going back at an angle.
To make this type of drawing, the student must first choose a face from which to draw the projection. Isometric dot paper can be used, with width and height having an equal scale.
For depth, the scale should be half of that for the width and height. For example, if the scale for height and length is 1 cm = 2 cm, (1:2) then the scale for depth will be 0.5 cm = 2 cm (0.5:2).
Source: translated from En avant les maths 7e année, CM, Sens de l’espace, p. 4-7.
Knowledge: Top View, Front View, Side View
Top views (plans) as well as front and side views (elevations) are “flat drawings” without perspective.
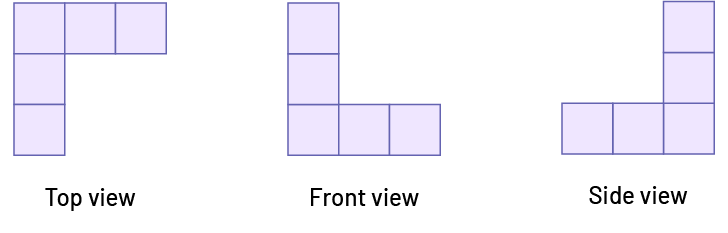image Top view:5 blocks are placed to form an upside down « L ».Front view: 5 blocks are placed to form an « L ».Side view: 5 blocks are placed so as to form an « L » whose opening is to the right.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Perspectives and Appropriate Scales
Scale drawing. A drawing in which the dimensions are proportionally reduced or enlarged from the original dimensions.
Perspective drawing. A perspective drawing shows three views (top, front, and side views) in one illustration. The two types of perspective drawing are isometric projection and cabinet projection.
Isometric projection. Isometric projections show an object from the “corner”, with the width and depth going off at equal angles. In isometric projections, a scale is applied consistently to all dimensions (for example, 1 cm:2 cm for the height, width, and depth).
Cabinet projection. A type of perspective drawing that shows an object “straight on”, with the depth going back at an angle. In a cabinet projection, the depth scale is half the width and height scale. For example, if the scale for width and height is 1:2, that is, 1 cm = 2 cm, then the scale for depth is 0.5:2, that is, 0.5 cm = 2 cm.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.